NOI 一轮复习 V：动态规划

本文是 NOI 一轮复习的第五篇，包括动态规划的状态设计和转移优化。

动态规划是 OI 最重要的部分之一。从学习与做题的角度来说，主要分为设计状态与优化两部分。其中前者更多的是做题和总结方法与套路，而后者相对吃经验。

值得注意的是，很多题目都要求我们在设计算法以前先将题目进行一定的转化，从而将一个不熟悉的模型转化为我们更容易把握的模型。这一点在动态规划的题目中体现的尤为明显。

动态规划的状态设计

注意基本模型。

线性 DP

在线性结构上枚举每一维度进行转移的 DP。

对于任意一段后缀，其能对整个序列的最大前缀和产生贡献的都是其最大前缀和。

设 $f_{i,j}$ 代表考虑前 $i$ 个数，$[i+1,n]$ 的最大前缀和为 $j$ 的期望答案。可以以 $p_i$ 的系数转移到 $f_{i+1,\max\{j-1,0\}}$，$1-p_i$ 的系数转移到 $f_{i+1,j+1}$。

答案便是 $f_{i,0}$。代码。

背包

基本模型：01 背包、完全背包、多重背包、分组背包、方案数背包的撤回（将转移的东西减去即可）。

为方便分析时间复杂度，记 $M=\max\{C,D\}$。

考虑 $K=0$ 怎么做。分别考虑划分两种特征，两次背包分别对工具箱和螺丝进行 DP 即可。

发现 $K$ 很小，考虑针对它设计状态。对于不是这 $K$ 个没事找事的螺丝，前面的 DP 做法依然成立。然后再考虑这些没事找事的。

设 $F(i,j,k)$ 代表考虑前 $i$ 个工具箱，普通螺钉的重量为 $j$，三角螺纹的重量为 $k$。需要枚举当前的选的东西是什么和上一个东西是什么。滚掉 $i$ 这一维，所有状态都是可以转移的，考虑用这种方式处理没事找事的螺丝，时间复杂度为 $O(k^2 w M)$。

然后枚举体积，进行背包合并即可。代码。

区间 DP

区间 DP 有两种，分别是从两边扩展和中间枚举断点的。如果信息可以“合并”，那么大概率是区间 DP。

不难想到区间 DP，考虑 $g_{l,r}$ 代表 $[l,r]$ 的最小剩余数和栈大小。转移时可以直接将 $l$ 或 $r$ 放进栈中，也可以在 $[l,r]$ 中寻找一个 $i$ 与 $l$ 或 $r$ 删除。以 $a_l$ 和 $a_i$ 配对为例，考虑保留一段 $[i+1,j]$ 或者是 $[j,i-1]$，则需要将剩下的两端完全删除，中间会夹一个 $i$ 和另一端需要处理的内容，判断两端是否完全删除依然可以采用区间 DP。时间复杂度为 $O(n^6)$，但是非法状态很多，可以通过。代码。

图上 DP

• 树上 DP
  • 一般按照拓扑序进行求解，注意合并时是加边还是加点。
  • 换根 DP。如果一条边的贡献可以很简单的转化，那么可以简单将 DP 的根换走。
• DAG & 图 上 DP
  • 图可以考虑缩点成 DAG，然后按照拓扑序进行 DP 即可。

只有两种情况：

1. 两条路径存在一个点重合。这样只要找到根出发的前四大链即可。
2. 不存在重合。考虑枚举子树，其中一条路径经过这个子树的根，然后子树外再找一条最优路径。

状态列表：

• $dp_x$ 表示考虑 $x$ 为根的子树去掉一条一个端点为 $x$ 的最大连通块数；
• $mx_{x,k}$ 代表以 $x$ 为根的子树中，$dp(y)$ 的 $k$ 大值；
• $fp_x$ 代表去掉一条经过 $x$ 的链的最大连通块数；
• $f_x$ 代表去掉子树内一条路径的最大连通块数，需要记录儿子中最大的 $f$ 来进行转移。

发现当 $x$ 是否不是根会直接影响 $f$ 的答案，依次记录 $f_{0/1}$ 来解决这个问题。

以上所有状态均可以换根计算。为了换根，需要记录 $fmx$ 的次大值。换根过程异常麻烦。

int n, ans; 
vector<int> G[100005]; 
int dp[100005]; // 去掉一个以 x 为端点的链后连通块最大数量
int mx[100005][4]; // 以 x 为根，dp(y) 的 k 大值 
int fp[100005]; // 去掉经过 x 的路径后连通块最大数量
int f[100005][2]; // x 的子树中最大连通块数量 / 删掉 x 之后 x 外面还有连通块
int fmx[100005][2]; // f[y][1] 最次大值

inline void change(int x, int v) {
    for (int i = 0; i < 4; ++i)
        if (mx[x][i] < v) swap(mx[x][i], v); 
}
inline void fchange(int x, int v) {
    for (int i = 0; i < 2; ++i)
        if (fmx[x][i] < v) swap(fmx[x][i], v); 
}

void dfs(int x, int fa) {
    dp[x] = mx[x][0] = mx[x][1] = mx[x][2] = mx[x][3] = -INF; 
    fp[x] = f[x][0] = f[x][1] = fmx[x][0] = fmx[x][1] = -INF; 
    int cnt = 0; 
    for (int y : G[x]) if (y != fa) {
        dfs(y, x); ++cnt; 
        change(x, dp[y]); fchange(x, f[y][1]); 
    }
    dp[x] = max(cnt, mx[x][0] + cnt - 1); 
    fp[x] = max(dp[x], mx[x][0] + mx[x][1] + cnt - 2); 
    f[x][0] = max(fp[x], fmx[x][0]); 
    f[x][1] = max(fp[x] + 1, fmx[x][0]); 
}

void dfs2(int x, int fa) {
    int sum = G[x].size(); ans = max(ans, sum); 
    for (int i = 0; i < 4; ++i) ans = max(ans, sum += mx[x][i] - 1); 
    int cnt = G[x].size() - 1; 
    for (int y : G[x]) if (y != fa) {
        int p = -1; 
        for (int i = 0; i < 4; ++i) if (mx[x][i] == dp[y]) p = i; 
        int mx0 = mx[x][0], mx1 = mx[x][0] + mx[x][1], mx2 = fmx[x][0]; 
        if (p == 0) mx0 = mx[x][1], mx1 = mx[x][1] + mx[x][2];  
        if (p == 1) mx1 = mx[x][0] + mx[x][2]; 
        if (fmx[x][0] == f[y][1]) mx2 = fmx[x][1]; 
        dp[x] = max(cnt, mx0 + cnt - 1); 
        fp[x] = max(dp[x], mx1 + cnt - 2); 
        f[x][0] = max(fp[x], mx2); 
        f[x][1] = max(fp[x] + 1, mx2); 
        ans = max(ans, f[x][0] + fp[y]); 
        change(y, dp[x]); fchange(y, f[x][1]); 
        dfs2(y, x); 
    }
}

动态 DP

依然设 $f_{i,1/0}$ 代表对于 $i$ 的子树是否选则第 $i$ 个节点，子树内的独立集最大大小。

如何支持修改？对原树进行重链剖分，设 $g_{i,1/0}$ 代表 $i$ 的子树不考虑重儿子的情况下的答案。有：

$$f_{i,0}=g_{i,0}+\max\{f_{son_i,0},f_{son_i,1}\}\\ f_{i,1}=g_{i,1}+f_{son_i,0}$$

我们定义另一种矩阵乘法（将其称为 $\max,+$ 卷积，需要满足 $+$ 有结合律，$\max$ 对 $+$ 有分配律）：

$$C_{i,j}=\max_{k=1}^n A_{i,k}+B_{k,j}$$

则有：

$$\begin{bmatrix} f_{son_i,0} & f_{son_i,1} \end{bmatrix}\times \begin{bmatrix} g_{i,0} & g_{i,1}\\ g_{i,0} & -\infty \end{bmatrix}= \begin{bmatrix} f_{i,0} & f_{i,1} \end{bmatrix}$$

这样在一条重链上就可以直接用线段树维护答案。我们相当于从一个权值为 $0$ 的叶子节点开始 DP，修改时，当前节点的 $g_{i,1}$ 会改变，然后直接考虑重链顶端父亲的答案改变，改的是当前节点的一个轻儿子，计算改变量即可。

void dfs(int x, int fa) {
    siz[x] = 1; ::fa[x] = fa; f[x][1] = a[x]; 
    for (int i = hd[x]; i; i = nxt[i]) { int y = to[i]; if (y != fa) {
        dfs(y, x); siz[x] += siz[y]; 
        if (siz[y] > siz[son[x]]) son[x] = y; 
        f[x][1] += f[y][0]; 
        f[x][0] += max(f[y][0], f[y][1]); 
    }}
}
void dfs2(int x, int topf) {
    idx[L[x] = ++num] = x; R[top[x] = topf] = num; 
    g[x].a[0][1] = a[x]; g[x].a[1][1] = -INF; 
    if (!son[x]) return; dfs2(son[x], topf); 
    for (int i = hd[x]; i; i = nxt[i]) { int y = to[i]; if (y != son[x] && y != fa[x]) {
        dfs2(y, y); 
        g[x].a[0][1] += f[y][0]; 
        g[x].a[0][0] += max(f[y][0], f[y][1]); 
    }}
    g[x].a[1][0] = g[x].a[0][0]; 
}

inline void update(int x, int k) {
    g[x].a[0][1] += k - a[x]; a[x] = k; 
    while (x) {
        int y = top[x]; Matrix lst = T[rt[y]].dat; 
        update(rt[y], L[y], R[y], L[x]); Matrix now = T[rt[y]].dat; 
        x = fa[y]; 
        g[x].a[0][0] += max(now.a[0][0], now.a[0][1]) - max(lst.a[0][0], lst.a[0][1]); 
        g[x].a[1][0] = g[x].a[0][0]; 
        g[x].a[0][1] += now.a[0][0] - lst.a[0][0]; 
    }
}

其它 DP

一些杂项内容。

插入法

一种较为特殊的状态设计方法，大概类似于 $f_{i,j}$ 表示 $i$ 个数划分成 $j$ 段的方案数。

常规方法并不好处理，考虑一种以插入为转移的 DP。设 $f_{i,j}$ 代表考虑前 $i$ 个数，将序列划分成 $j$ 段的方案数。

考虑从 $1\sim n$ 依次放置数。一个数可以用来新增一个段（如果首尾已经放了 $s,t$ 就不能再放），也可以用来合并段（$j$ 种选择）。如果它是 $s,t$ 那么只能将它放到首尾。

最终答案为 $f_{n,1}$。

for (int i = 2; i <= n; ++i)
    if (i != s && i != t) {
        for (int j = 1; j <= i; ++j) { 
            int c = (i > s) + (i > t);  
            f[i][j] = (1ll * j * f[i - 1][j + 1] + 1ll * (j - c) * f[i - 1][j - 1]) % P; 
        } 
    } else {
        for (int j = 1; j <= i; ++j)
            f[i][j] = (f[i - 1][j - 1] + f[i - 1][j]) % P; 
    }

数位 DP

求解值域中满足某个条件的数的个数。采用 DFS 实现，枚举当前位数和各类信息。

CF1815D XOR Counting。$m\ge 3$ 有 $\frac{n-k}{2},\frac{n-k}{2},k$，因此只需要考虑 $m=2$。按照每一位去填写，计算 $f,g$ 代表答案和能异或出的数量。按照 $n$ 的奇偶性去讨论即可。代码。

---

对于有进位数位 DP，一般采用递推。

ARC153D Sum of Sum of Digits。设 $f_{x,i}$ 代表第 $x$ 位恰好有 $i$ 个数进位时末尾 $x$ 位数的答案，然后进位的一定是排序后的前几个。代码。

轮廓线 DP

例题

难度可能比较大。

[ABC313Ex] Group Photo

Portal.

序列可以重排列，直接按照顺序递推便不太能做。但是要钦定一个顺序，发现按值的大小很适合。不难想到插入法。

设 $f_{i,j}$ 代表填前 $i$ 个元素，有 $j$ 个段满足原题条件的方案数，考虑 $a_{i+1}$ 填到哪里（此时 $b$ 应该填 $b_{i+j+1}$）：

• 将其放到一个连续段的左侧或者右侧，$f_{i+1,j}\stackrel{+}{\leftarrow}f_{i,j}\times 2\times j$，需要满足 $b_{i+j+1}>a_i$ 才能满足条件；
• 合并两个连续段，$f_{i+1,j-1}\stackrel{+}{\leftarrow}f_{i,j}\times (j-1)$，没有任何条件就可以转移；
• 新增一个连续段，$f_{i+1,j+1}\stackrel{+}{\leftarrow}f_{i,j}\times (j+1)$，需要满足 $\min\{b_{i+j+1},b_{i+j+2}\}>a_i$。

$a,b$ 均从小到大排序即可转移。代码。

[AT DP] Subtree

Portal.

由于逆元不一定存在，所以设 $f_i$ 代表以 $i$ 为根的子树内染黑点的方案数，$g_i$ 代表 $i$ 子树外的方案数。然后直接树形 DP 和换根即可。代码。

动态规划的转移优化

虽然套路非常多，但无非就两种：针对单调性的优化和数据结构优化。

wqs 二分

我们可以使用 wqs 二分对 DP 进行降维。

wqs 二分的状态的其中一维是物品个数。这是它的明显标志，因此它比较套路。$f_i$ 表示恰好（最多/至少）选取 $i$ 个物品时的答案，如果 $f$ 是凸函数那么则可以使用 wqs。我们可以猜测 $O(nk)$ 过不去就是凸的，或者也可以打表。

由于 $f$ 是凸的，因此我们可以选择二分斜率，以此计算出它的切线。有时它能直接用，有时可以对 DP 进行降维，有时和斜率优化等内容一起出现。

具体来说，我们画出所有点 $(i,f(i))$，假设它们构成一个上凸壳。二分斜率 $k$，发现随着 $k$ 的减小，直线的切点会越来越靠右。

因此二分 $k$ 直到横坐标切到我们想要的位置（比如恰好选择 $m$ 个数），那么此时的纵坐标就是答案了。

如何求出切点？我们希望这个切点的 $y$ 坐标最大，也就是在 $y$ 轴上的截距最大。设截距为 $g(x)$，那么切点 $(x,f(x))$ 在 $y$ 轴上的截距就是 $g(x)=f(x)-kx$。问题就是如何求出 $g(x)$ 的值了。

考虑 $g(x)$ 的意义，相当于钦定的 $x$ 个物品的代价都比原来少 $k$，$g(x)$ 相当于每个物品代价减 $k$ 之后的最优解。

$l,r$ 如何调整？要逼近 $(m,f(m))$ 如果此时切点 $(x,f(x))$ 满足 $x<m$ 时，那么应该将斜率减小，才能让切点右移。

[ARC168E] Subsegments with Large Sums

Portal.

直接 wqs，错了，因为不是凸的。

二分答案，现在是说，答案为 $x$，是否能够划出 $k$ 个连续段？设 $f_n$ 划出 $x$ 个段满足条件，最小的代价。为 $f_n\le n -k$ 时合法，wqs 二分即可。代码。

决策单调性优化

决策单调性分治常见于 2D / 1D 动态规划，其中一维是转移层数，且从一层仅转移至下一层。

如果有决策单调性，那么应该使用四边形不等式去证明，但是一般来讲 assert 可能更有说服力。

如果采用分治实现，那么应该满足在计算 $f_i$ 的时候 $f_{0\sim i-1}$ 全部已知。如果不能，则需要套上一层 CDQ 分治（也就是要求半在线）。这样的时间复杂度是 $O(n\log^2 n)$，但是其优点是可以快速计算无法计算答案，但是可以快速计算增量的贡献，直接跟踪分治中心计算即可。

如果区间贡献可以直接快速计算，那么我们使用二分栈或者二分队列即可，时间复杂度 $O(n\log n)$。大概就是维护一堆三元组，表示某个区间的转移点是什么。

SMAWK 算法 可以用 $O(n)$ 的时间复杂度完成决策单调性 DP，但是不太常见。

[PA 2022] Nawiasowe podziały。经典的划分区间段问题，答案是关于 $k$ 上凸的，wqs 二分解决。里面有决策单调性，要进行 $k$ 轮，但是只需要知道前面的对后面的影响，CDQ 分治降维即可。代码。

斜率优化

如果一类最优化 DP 可以写成 $f_i=\min\{f_j+cost_j+cost_i\}+F_iF_j$，那么可以改写成 $f_j+cost_j=F_iF_j+(f_i-cost_i)$，可以视作 $y=kx+b$。也就是说，支持加入点 $(x,y)$，查询当前直线经过某个点时候 $y$ 轴截距最大或者最小。

如果每次询问的直线的斜率单调，且每次加入的横坐标单调，那么可以单调队列维护；否则可以考虑李超树。

[HNOI2008] 玩具装箱，直接做即可。代码。

数据结构优化

如果我们可以使用数据结构快速计算转移的代价，那么便可以直接优化，常见的如单调队列优化。

[NOIP2023] 天天爱打卡。设 $f_i$ 代表前 $i$ 个的最优代价，直接线段树优化即可。代码。

---

另一个常见的内容是，转移方程和同层无关，那么可以直接整体转移，这样的方式称为整体 DP。

动态规划杂项

一些动态规划的杂项内容。

自动机上 DP

我们可以在字符串自动机（KMP 自动机、AC 自动机等）上进行 DP，DP 自动机上也是可以的。

人脑自动机

设 $p$ 的 LIS 长度为 $K$，那么应该有 $a_i\in [K,K-1]$。我们将 $a_i\leftarrow a_i-K$。

排列上的数可以划分成四种类型：

只有绿点和红点可以让 $K$ 增加，只有绿点在 $a$ 处填写的是 $-1$，其余都是 $0$。

让红黑匹配尽可能地先出现，也就是说只让黑点靠着红点出现，那么 $f_{i,k}$ 代表其结尾的性质为 $i$，当前 $K=k$，考虑人脑建出自动机：

• $i=0$，放了一个绿，下一个什么都能放。
• $i=1$，放了一个红，下一个只能是黑色。
• $i=2$，放了一个蓝，下一个只能放绿或蓝。放蓝的话，就不能再放红黑对了。
• $i=3$，放完红黑对了，那么下一个点只能放绿色或蓝色。再放一个蓝，则不能放置红黑对了。因为我们需要尽可能让红黑对出现在前面。

实际上，蓝蓝红黑和红黑蓝蓝是等价的状态（转移 $3$），蓝红黑和红黑蓝也是等价的状态，黑点只是为了给红点提供一个匹配，来保证其在删去后不会让 $a$ 的值发生改变。这是这样转移的原因。

如何统计答案？首先最后不能停留在 $1$，然后对于 $K=2,n-1$ 进行一个特判即可。代码。

DP 套 DP

本质上就是内层 DP 的结果作为外层 DP 的状态，内层压的东西一般可以看成一个 bool 数组，表示外层的状态是否能够取到，外层在内层 DP 建成的 DP 自动机上进行 DP。这样状态数可能很多，所以往往需要以实际搜出来的结果为准。

LCS 是什么？像这样：

$$\text{LCS}_{x,y}= \begin{cases} \text{LCS}_{x-1,y-1}+1&,A_x=B_y,\\ \max\{\text{LCS}_{x-1,y},\text{LCS}_{x,y-1}\}&,A_x\neq B_y.\\ \end{cases}$$

我们对 LCS 取一遍前缀最大值。把这个 LCS 的 DP 数组作为状态压进 DP（当其中一维固定时，LCS 数组的前缀最大值差分后可以得到一个 01 序列，状压后就可以压进去）。这相当于自动机上的一个点，枚举出满足不出现子串 NOI 的字符作为自动机的转移，计算出转移到的自动机上的点并更新方案数。

int n, k, ans[20], a[20], b[20]; // LCS(i, ...)
char s[20];
int f[2][35005][3]; // 考虑到字符串的第 i 位，当前 "NOI" 子串的长度为 k

void decode(int *a, int ret) {
    for (int i = 0; i < k; ++i) a[i + 1] = (ret >> i & 1) + a[i];
}
int encode(int *a) {
    int ret = 0;
    for (int i = 0; i < k; ++i) ret |= (a[i + 1] - a[i]) << i;
    return ret;
}
void dp(int now, int t, int p, char c, int w) {
    decode(a, t);
    for (int i = 1; i <= k; ++i) b[i] = max({b[i - 1], a[i], a[i - 1] + (c == s[i])});
    t = encode(b); f[now][t][p] = (f[now][t][p] + w) % P;
}

int main(void) {
    scanf("%d%d%s", &n, &k, s + 1); f[0][0][0] = 1; 
    for (int i = 0; i < n; ++i) {
        memset(f[i - 1 & 1], 0, sizeof(f[i - 1 & 1]));
        for (int j = 0; j < 1 << k; ++j) {
            if (f[i & 1][j][0]) {
                dp(i - 1 & 1, j, 1, 'N', f[i & 1][j][0]);
                dp(i - 1 & 1, j, 0, 'O', f[i & 1][j][0]);
                dp(i - 1 & 1, j, 0, 'I', f[i & 1][j][0]);
            }
            if (f[i & 1][j][1]) {
                dp(i - 1 & 1, j, 1, 'N', f[i & 1][j][1]);
                dp(i - 1 & 1, j, 2, 'O', f[i & 1][j][1]);
                dp(i - 1 & 1, j, 0, 'I', f[i & 1][j][1]);
            }
            if (f[i & 1][j][2]) {
                dp(i - 1 & 1, j, 1, 'N', f[i & 1][j][2]);
                dp(i - 1 & 1, j, 0, 'O', f[i & 1][j][2]);
            }
        }
    }
    for (int i = 0; i < 1 << k; ++i) for (int j = 0; j < 3; ++j) {
        int &x = ans[__builtin_popcount(i)];
        x = (x + f[n & 1][i][j]) % P;
    }
    for (int i = 0; i <= k; ++i) printf("%d\n", ans[i]);
    return 0;
}

状态数优化

有时 DP 的效率不高不是转移不够高效（很多情况转移是无法优化的），而是状态数实在太多了。在这种时候我们往往考虑通过重新设计状态、合并等价状态、寻找有效的状态等方式来优化状态数。

建出合并二叉树，令左儿子合并到右儿子。附魔费用仅对非叶子节点有贡献，贡献是其左儿子的权值 $s(l_u)$。累计惩罚仅对非根节点有贡献，贡献是 $2^{d(u)}-1$。其中 $d$ 是指子树内距离最长的叶子。

设 $w(u)$ 代表叶子节点 $u$ 走到根节点走过了多少左儿子边，那么 $\sum_u s(l_u)=\sum_u a_u w(u)$。

当 $a$ 降序排序时，应该保证 $w$ 升序排序才能使得该值更小。现在我们有两种方法，一种是从叶子节点开始合并，另一种是从根节点开始分裂。

---

如果从叶子节点开始合并，那么设 $f_{i,s}$ 代表初始有 $i$ 本附魔书，当前 $w$ 的可重集为 $s$，而最后再在 $s$ 里 push_back 一个子树根节点的 $d(u)$ 时的最小累计惩罚之和。那么合并的时候直接暴力枚举左子树大小，左子树的所有 $w$ 都要 $+1$。剪枝时舍弃掉被偏序的状态。配合上 $w=1$ 可以获得 $75$ 分。

状态数爆炸的最重要原因是我们需要记录一个 $d$，自底向上无法得知这个 $d$ 是什么，因此我们考虑自顶向下对儿子进行分裂。我们总是取 $w$ 前若干小的进行分裂，这样一定更优。观察可得，如果分裂出新的树的大小为 $|T|$，之前累计惩罚为 $v$，那么新的累计惩罚为 $2v+|T|-2$。那么直接维护即可，配合上 $w=1$ 可以获得 $90$ 分。

注意到，如果之前某个节点分裂出了 $1$ 个儿子，那么它接下来必须分裂出不少于这个数量的叶子，剪枝，可以获得 $100$ 分。代码。

---

官方题解使用了暴力枚举分拆数，然后疯狂剪枝的方法，实际表现非常优秀，尚不知道其原理。

DP 思路总结

题车

对于对应的组别来说，中档题会附带一个星号，难题会附带两个星号。

由于 DP 的难度在于状态设计和套路积累，因此题会非常多。

刷基础 1

巩固所学内容，训练思维的熟练度和准确度。本身难度不大。

[CF1178F] Colorful Strip

Portal.

首先考虑 F1 的做法。条件非常特殊，每种颜色恰好会染上一个位置且有顺序，区间 DP 确定区间中第一个染的颜色，然后枚举左右段的长度给拼起来，拆一下贡献即可。代码。

对于 F2，颜色数并没有变化，考虑将相同的颜色段缩起来，然后先判掉无解的情况。然后设 $L_x,R_x$ 代表颜色出现的最左最右位置。一个区间 $[i,j]$ 是合法的当且仅当其最小颜色全部出现在 $[i,j]$ 内，最后再把中间段的贡献呈上去就行。代码。

[CF1280D] Miss Punyverse

Portal.

设 $f_{x,i}$ 表示以 $x$ 为根的子树内选择 $i$ 个连通块的最大满足要求的块数（除了 $x$ 所属的连通块）。$g_{x,i}$ 代表 $x$ 所属连通块的最大权值，树形背包随便跑一下就行。代码。

[CF1394D] Boboniu and Jianghu

Portal.

问题只是给相等的高度进行定向。设 $f_{i,0/1}$ 代表到 $i$ 父亲的边强制为连入/连出情况下的贡献和。先假定所有都选 $0$ 再枚举 $1$ 的数量即可。代码。

* [CF1845E] Boxes and Balls

Portal.

对于移动到目标状态，我们只需要消耗最小次数，剩下的来回交换刷分即可。

将问题抽象成这个东西：

• 初始前缀和序列 $s$，目标前缀和序列 $s'$；
• $\sum |s'-s|\le k$，
• $\sum |s'-s|\equiv k\pmod 2$。

设 $f_{i,j,k}$ 代表当前填前 $i$ 个数，填了 $j$ 个 $1$，$\sum |s'-s|=k$ 的方案数，考虑当前位填 $0/1$：

$$f_{i,j,k}=f_{i-1,j,k-|j-s_i|}+f_{i-1,j-1,k-|j-s_i|}$$

注意到 $|j-s_i|$ 的取值范围是 $O(\sqrt{k})$ 的，否则 $\sum$ 这堆东西会超过 $k$。只枚举这些值即可。代码。

[CF1778F] Maximizing Root

Portal。不难发现 $a_1$ 只能乘一次，因此我们要看它最大能乘个什么。进行一次暴力树形 DP，$f_{x,i}$ 代表给 $x$ 乘上约数 $i$ 的最小步数。本来不满足的最多有一次操作机会（乘上自己），转移时对于每个约数取个 $\min$ 即可。代码。

刷提升 1

稍有难度的题目。

* [CF1750F] Majority

Portal.

不知道这个条件怎么刻画，那看看如何刻画不合法序列：

1. 两端不全是 $1$；
2. 全是 $1$，但是操作到尽头时每一个连续 $0$ 段的长度都比两边连续 $1$ 段的长度之和大。

设 $f_{i,j}$ 代表长度为 $i$ 的序列，两端为 $1$，操作到最后最后一个 $1$ 连续段的长度为 $j$。这样答案就是 $f_{n,n}$。初始 $f_{1,1}=1$。

对于 $f_{i,i}$，考虑容斥，有：

$$f_{i,i}=2^{i-2}-\sum_{j=1}^{\lfloor(i-1)/2\rfloor}f_{i,j}$$

对于 $f_{i,j}$，前面一定有一个 $1$ 连续段接 $0$ 连续段 的东西，枚举 $0$ 的长度 $k$ 和 $1$ 的长度 $l$，那么有：

$$\begin{aligned} f_{i,j}&=f_{j,j}\times \left(\sum_{j+k<i}\sum_{j+l<k}f_{i-j-k,l}\right)\\ &=f_{j,j}\times \left(\sum_{k=j+2}^{i-j-1}\sum_{l=1}^{k-j-1}f_{i-j-k,l} \right)\\ &=f_{j,j}\times \sum_{(i-j-k)+l<i-2j}f_{i-j-k,l} \end{aligned}$$

前缀和优化即可。代码。

* [CF1809G] Prediction

Portal.

对于一个合法的排列 $p$，删除 $a_{p_i}$ 最小的 $p_i$，新的 $p'$ 必定合法。

设 $f_{i}$ 代表填完 $(i,n]$ 的方案数，初始 $f_n=1$，考虑 $a_i$ 填的位置：

1. 不填在当前第一个位置，不影响后面元素的前缀 $\max$，$f_{i-1}\stackrel{+}{\leftarrow} f_{i}(n-i)$；
2. 填在当前第一个位置。设 $lst_i$ 代表最大的 $j$ 使得 $a_i-a_j>k$，那么 $(lst_i,i)$ 都需要出现在 $i$ 之前，则 $i-lst_i-1$ 需要填入 $n-lst_i-2$ 个位置（除了第一个）。

双指针求 $lst$，时间复杂度 $O(n)$。代码。

[CF1372E] Omkar and Last Floor

Portal.

一列聚集在一起一定是最优的，考虑 $f_{i,j}$ 代表区间 $[i,j]$ 的答案，$c_{i,j,k}$ 代表左右端点都在 $[i,j]$ 且经过第 $k$ 列的区间数量。

枚举聚集的那一列，那么：

$$f_{i,j}=\max\{f_{i,k-1}+c_{i,j,k}^2+f_{k+1,j}\}$$

$c$ 区间 DP 时容斥一下就行。代码。

* [CF1188D] Make Equal

Portal.

记 $b_i=\max a - a_i$，那么要求：

$$\sum_{i=1}^n \operatorname{popcount}(x+b_i)$$

考虑二进制下的第 $k$ 位：

• $x$ 的第 $k$ 位是否填 $1$；
• $b_i$ 的第 $k$ 位是否填 $1$;
• 第 $k-1$ 位是否进位。

第 $k-1$ 位的进位情况和 $b_i\bmod 2^k$ 有关。我们按照这个东西排序，能进位的就是 $b$ 的一段前缀。

设 $f_{i,j}$ 代表有 $j$ 个数进位到第 $i$ 位的答案。考虑 $x$ 当前这一位填 $1$ 还是填 $0$，贡献随便算一下就行了。代码。

* [CF1517F] Reunion

Portal.

设一种方案 $S$ 的半径为 $f(S)$，那么答案是 $\sum_{r=1}^{n}\sum_{S}[f(S)\ge r]$。实际上我们只需要对于每个 $r$ 分别计算即可。

设 $f_{i,j}$ 代表 $i$ 的子树距离 $i$ 最近的黑点距离为 $j$ 的方案数，记满足 $j=r+1$ 的为预备点，$g_{i,j}$ 表示 $i$ 子树内最深预备点与 $i$ 距离为 $j$ 时的方案数。

值得注意的是，若子树内已经存在预备点，那么没有必要再考虑距离 $i$ 最近的黑点与 $i$ 的距离。不存在时，这东西才需要被记录。

考虑使用树形背包的方式合并：

• 合并 $f_{x,i},f_{y,j}$，可以转移到 $f_{x,\min \{i,j+1\}}$；
• 合并 $g_{x,i},g_{y,j}$，可以转移到 $g_{x,\max\{j,k+1\}}$；
• 合并 $f_{x,i},g_{y,j}$，如果 $i+j+1>r$，那么 $g$ 定义的预备点是符合限制的，其会转移到 $g_{x,j+1}$，否则会转移到 $f_{x,i}$；
• 合并 $g_{x,i},f_{y,j}$ 大致同理。

答案是 $\sum g_1$。

时间复杂度 $O(n^3)$。代码。

[P2664] 树上游戏

Portal.

考虑换根 DP。维护数组 $a_x$ 表示当前根 $rt$ 确定之后，颜色 $x$ 对于 $rt\rightarrow i(i\in [1,n])$ 的贡献之和。

换根时只需要维护在 $x$ 的子树中，$c_{fa(x)}$ 的贡献即可。代码。

刷提升 2

接着提升自我吧！

[CEOI2005] Mobile Service

Portal.

DP 是简单的，问题是空间如此之小，方案该怎么记录？

首先，方案数组是不可能被滚动的。但是决策数量比较小，可以使用 unsigned char 来记录。然后发现只记录一个数就可以了。代码。

* [eJOI2018] 护照

Portal.

不难想到状压，而且 $P\le 2$，因此 $P=2$ 时只需要枚举子集然后对于子集和补集合并状压 DP
数组即可，因此这里只需要考虑 $P=1$。

设 $f_i$ 代表集合 $i$ 中的签证全部办理完成后的最小结束时间。转移采用刷表法，考虑限制是什么：一个时间内，旅行和办理签证做多做一种。如果我们依次检查其它国家的限制，那么时间复杂度为 $O(n^2 2^n)$。

但如果按照 $t$ 从小到达考虑，这个过程显然是具有单调性的。考虑从限制本身入手：

1. 办理签证的时间不可以撞到出国的时间。
2. 如果 $p$ 正在办理签证，那么这个时间不能考虑办理签证。

将 $l$ 排序之后维护两个指针来限制两条限制，找到可以办理当前签证的最小时间即可。

这样就可以 $O(n2^n)$ 完成了。代码。

[ARC108E] Random IS

Portal.

求的是依次随机选择排列中合法的数，然后 IS 的期望长度。

设 $f_{l,r}$ 代表 $l,r$ 已经被选择，那么有：

$$f_{l,r} = \frac{\sum_{a_l<a_k<a_r} f_{l,k}+f_{k,j}+1}{g_{l,r}}$$

可以在 $k$ 处新增一个 $1$。所有的东西都可以很方便地用树状数组求出，代码。

[Ptz 2020 Summer Day4] Ternary String Counting

Portal.

$O(n^4)$ 直接 $f_{i,x,y,z}$ 记录每一个字符出现的位置，$O(n^3)$ 记录前两个不同字符的出现位置。都需要前缀和优化。

状态数还是过多了，我们需要寻找一个方式简化。先把转移写出来：

• $f(i+1,i,k)\stackrel{+}\leftarrow f(i,j,k)$；

• $f(i+1,i,j)\stackrel{+}\leftarrow f(i,j,k)$；

• $f(i+1,j,k)\stackrel{+}\leftarrow f(i,j,k)$。

再考虑题目中的限制，实际上就是限制了 dp 过程中 $j$ 和 $k$ 的取值范围：

1. $x=1$，则 $j<l$；
2. $x=2$，则 $j\ge l,k<l$；
3. $x=3$，则 $k\ge l$。

考虑优化，看上去第一维什么都不是！将转移分为 $i$​ 层，每一层的状态只能从上一层转移过来，第三个转移就是直接从上一层的对应点转移，第一二个转移是对上一层的一列和一行求和。

等价于，每次给出一个矩形，先把矩形外的值全部清零。然后还可以发现，一旦某个值被清零，那么这个值以后永远都是零。并且对于某一行来说，非零的值永远是一段连续区间，而且其位置是单调的。

双指针扫，不重复清零某个行即可。最终时间复杂度 $O(n^2+m)$。代码。

[Ptz 2022 Summer Day3] Counting Sequence

Portal.

对于 $O(n^2)$，直接设 $f_{i,j}$ 表示当前 $\sum =i$，结尾是 $j$ 的贡献。

当 $a_1\ge B$ 时，序列长度为 $O(n/B)$，可以设计序列长度的 DP。设 $g_{i,j,S}$ 表示到序列第 $i$ 位，当前和 $a_1$ 的差为 $j$，$\sum a_t - a_1 = S$ 的方案数，转移枚举最后一个填什么，复杂度 $O((n/B)^4)$。根号平衡可以做到 $O(n^{8/5})$。

改为 $g_{i,j}$ 代表长度为 $i$，$\sum a_t-a_1=j$，然后在序列前面插入一个数。注意 $f$ 可以按照 $i \bmod 2B$ 进行统计。代码。

刷提升 3

更偏向 DP 的优化。

刷能力

DP 综合应用。

* [ZJOI2019] 麻将

Portal.

可以发现其两部分是割裂的：判断胡牌和计数 DP。由于胡牌集合的大小只有 $13$，因此如果我们能解决判定问题，那么便可以建立自动机在上面解决计数问题。

先解决判定问题。七个对子只需要开一个桶即可，一个对子四个面子可以考虑使用 DP 来解决：设 $f_{i,j,k,0/1}$ 代表考虑前 $i$ 种牌，目前还剩下 $j$ 组 $(i-1,i)$ 和 $k$ 张 $i$，以及是否选择出了一组对子，这种时候的最大面子数。由于 $j\ge 3$ 或者 $k\ge 3$ 时都可以直接组成新的面子，因此状态中 $j,k\in [0,2]$。因此在一个状态中建立两个 $3\times 3$ 的二维数组即可。转移时将 $x$ 张 $i$ 牌添加进来即可。

牌种类数足够多时状态就被列举完了，因此直接暴力 DFS 拓展出所有状态即可，按照笔者的实现，其状态只有 $S=3956$ 种，而接下来的分析让我们知到我们只需要不胡的状态，其只有 $S=2091$ 种。

接下来我们要解决计数问题。我们需要知到第一个胡牌的位置，这并不好直接计算。设 $P(i)$ 代表恰好 $i$ 步胡牌的概率，那么：

$$\begin {aligned} E(x)&=\sum_{i=0}^{+\infty} i\times P(i)\\ &=\sum_{i=0}^{+\infty}\sum_{j=i}^{+\infty}P(j) \end{aligned}$$

可以发现第二个和式的意思是 $i-1$ 步没胡的概率，设 $f_{i,j,k}$ 代表选择前 $i$ 种牌，一共 $j$ 张，位于自动机上的状态 $k$，转移时选择 $t$ 张 $i$ 牌，系数是 $\dbinom {4-a_i}{t}$，令 $m=4n-13$，$f_i$ 为 $i$ 张牌没胡的方案数，则答案为：

$$ans=\frac{\sum_{i=0}^m f_i i!(m-i)!}{m!}$$

代码。

[CF924F] Minimal Subset Difference

Portal.

* [JOISC2020] Ruins 3

Portal.

旋风牛马大数数。

考虑从后往前扫，然后假定 $1\sim h$ 的石柱各出现了一根，那么接下来出现的 $\le h$ 的柱子，都会直接震没。那些没有被震死的柱子称为“标准柱”。

继续观察性质。如果当前位置为 $x$，后面存在 $x\sim x-k$，那么 $x$ 会下降到 $x-k-1$。

设 $f_{i,j}$ 代表后 $i$ 个柱子，此时 $h=j$ 的方案数。

我们先假定两根高度相同的柱子实际上是不同的，那么最终答案除以 $2^n$ 即可。

倒着 DP，设此时有 $c_0$ 个钦定消失，$c_1$ 个钦定存在。

1. $i$ 钦定消失，此时 $j$ 不变，有 $j$ 个可用高度，那么不算当前这个没消失的，这里可以填写 $j-(c_0-1)$ 个有效的。
2. $i$ 钦定保留，令 $h_i$ 代表 $i$ 最后的高度，分讨：
   • 如果 $h_i>j+1$，那么从 $f_{i+1,j}$ 转移，这里的贡献留给以后再计算。
   • 否则此时 $h_i=j+1$，那么此时枚举一个新增的大小 $k$，转移到 $f_{i,j+k}$，系数是：
     • 选择哪些位置的值被记入了当前 $j$。钦定除了当前位置的那 $k-1$ 个位置的方案数 $\dbinom{c_1-1-j}{k-1}$；
     • $j+2\sim j+k$ 的高度之前均有出现过一次，这里还可以选择各一次，然后还可以选择两个 $j+1$ 的高度，方案数是 $k+1$；
     • 固定那 $k-1$ 个位置上的数的排列，那些数都没有被震没。因此就是要求一个 $g_n$ 代表有 $2n$ 个数进行选择，然后震成值域连续段的初始方案数。

设 $g_{i,j}$ 代表用 $1\sim i$ 的数填 $j$ 个位置，放进去的最大数不影响原来能震成的值域连续段，那么能震成值域连续段的充要条件是 $i\ge j$。枚举第 $i$ 个数填了 $0/1/2$ 的转移方式：

$$g_{i,j}=g_{i-1,j}+2j\times g_{i-1,j-1}+j(j-1) g_{i-1,j-2}$$

代码。

[Ptz 2023 Winter Day6] 5

Portal.

不难设计出 $f_{len,sum}$ 这样的状态，但是状态数就成 $O(nS)$ 了，直接寄了。

可以发现 $1$ 出现的次数是比较少的，因此可以设计出一个 $f_{sum-len,len}$ 的状态，然后维护每个 $sum-len$ 对应的 $len$ 连续段（只有 $4$ 个），二进制拆分优化多重背包即可。代码。

刷综合

有些题目比较癫狂。

[NOI2022] 移除石子

Portal.

首先需要会判定是否合法。我们发现直接将恰好改为至多基本上不会错，因为可以将多的扔到一个位置然后用 $1$ 操作处理。事实发现也只需要特判很少的情况。

设 $f_{i,j,k}$ 代表考虑前 $i$ 个石子，统计第 $i$ 个位置出发和结束的 $2$ 操作，第 $i$ 个位置至少被 $j$ 个连续消除覆盖，第 $i+1$ 个位置至少被 $k$ 个覆盖的时候，至少需要添加多少个石子。

由于至少 $2$ 枚石子的时候就可以使用操作 $1$，因此猜测 $j,k\le 2$，事实也确实如此。

写一下需要特判的情况，$k=1$ 时会在全零和 ${1,1,1}$ 矛盾，$k>1$ 都可以通过移除至多一个二操作，然后剩下的用一操作消除的方式解决。

然后把 $f$ 的自动机建立出来，发现 $a_i\ge 8$ 的时候本质相同，直接转移即可。代码。

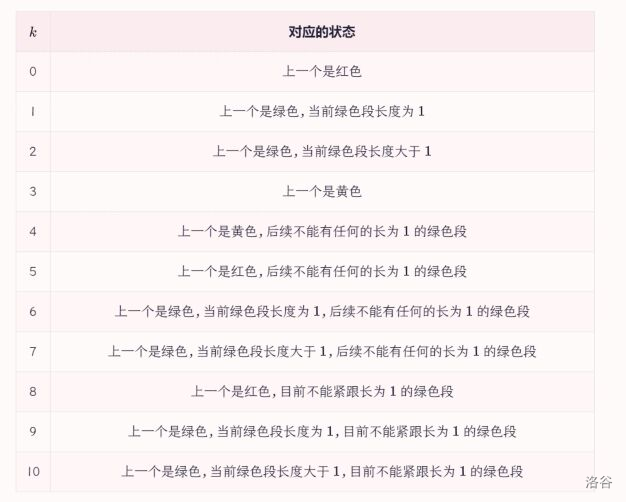
* [Luogu P8554] 心跳

Portal.

我们考虑去掉一个数之后前缀最大值改变的情况。

设 $k$ 为原先前缀最大值的个数，那那么只有当其原先是前缀最大值时，前缀最大值将变成 $[k-1,n]$。

尝试找出 $a$ 的合法结构，对于 $a$ 进行染色：

• 红色：原来就是前缀最大值的位置，可以使得 $k$ 增大 $1$；
• 绿色：用来代替红色点称为前缀最大值的位置，$k$ 不变；
• 黄色：垃圾，$k$ 不变。

可以发现，红色后面会接一段长度为 $x$ 的绿色，且它们的大小是递增的，然后再是一堆黄色，然后是下一个红色。绿色的出现条件是小于上一个红色但是大于上上个红色，黄色应该小于上一个绿色或者小于上上个红色。于是将颜色序列转化为 $p$ 时，一定可以构造出来。

尝试构建颜色序列和 $a$ 之间的双射，为什么一个颜色序列对应恰好一个合法的 $a$？首先我们构造 $a$，非红色点 $a_i=k$，红色点 $a_i=k-1+x$。

需要保证一个 $a$ 只能对应一种颜色序列，和 AGC055C 一样，我们限制等价状态。要注意情况不完全一样，因为 $a$ 可以改的值更多（以下 X 指非绿的东西）：

• 黄红绿 X 和红绿黄 X 是等价的状态，因此前者不可能出现（目前不能紧跟长度为 $1$ 的绿色段）；
• 如果出现了黄黄，那么就不能再填红绿 X 段了（后续不能有任何长度为 $1$ 的绿色段）。

另外，第一个数一定是红色，第二个数一定不能是黄色，因为序列头被删了自然就有了新的前缀最大值。

我们还需要限制 $m$，于是我们只需在自动机上只需要记录这些信息：

• 前面一个的颜色；
• 是否出现过黄黄；
• 这个绿色段的长度是 $0,1$ 还是大于等于 $2$；
• 当前绿色段前面的红色是否在黄色后面；
• 当前的红色个数。

要么 $k>m$，要么 $k=m$ 且没有不接绿色的红色，跑两次即可。

状态可以压缩成下图，代码：

* [AGC047F] Rooks

Portal.

太精彩啦！

一个暴力做法是，枚举每个 $s$ 求答案，然后用一个 $O(n^2)$ 的区间 DP 代表吃掉 $[i,j]$ 内的车。

但是我们不需要对于每个起点都求一遍答案，直接将整个区间 DP 的过程倒过来即可。也就是说，预处理出每个点能走到的区间，然后扩展这个东西。

状态数是 $O(n^2)$ 的，似乎是尽头？否！观察转移的形式，一定形如下图：

状态数只有 $O(2n)$，直接转移即可。代码。