在图中,如何判断一张图是否连通?如果删掉某条边,它还连通吗?有向图呢?这些操作有什么特殊性质吗?本文将探讨以 Tarjan 算法为核心的有关图的连通性的问题和欧拉路问题。
除了 Tarjan 算法,并查集等内容也能解决一些图连通性问题,请参照笔者相关文章。
拓扑排序
别问我为什么把这个放到这里来讲,因为接下来很多题都要用到它。
严格意义上来说,拓扑排序不是一种排序。是对有向无环图(DAG),将 中所有顶点排成一个线性序列,使得图中任意一对顶点 和 ,若它们之间存在一条有向边 ,则 在线性序列中出现在 之前。
模板。
开一个队列记录所有入度为 的点,然后维护即可。这一过程被称之为 Kahn 算法。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m;
int in[105];
vector<int> G[105];
queue<int> q;
int main(void) {
while (scanf("%d%d", &n, &m) == 2 && n) {
memset(in, 0, sizeof(in));
for (int i = 1; i <= n; ++i) G[i].clear();
while (m--) {
int x, y;
scanf("%d%d", &x, &y);
G[x].push_back(y);
++in[y];
}
for (int i = 1; i <= n; ++i)
if (in[i] == 0) q.push(i);
while (!q.empty()) {
int t = q.front();
q.pop();
printf("%d ", t);
for (int i = 0; i < G[t].size(); ++i) {
--in[G[t][i]];
if (in[G[t][i]] == 0) q.push(G[t][i]);
}
}
putchar('\n');
}
return 0;
}拓扑排序也可以使用 dfs 实现,感兴趣的读者可以自行学习。
有的时候求的拓扑序要求字典序,这时候直接将队列改为优先队列即可。
无向图的连通性
给定无向图 ,如果 ,从图中删去节点 和与 关联的所有边之后, 被分裂成两个或两个以上的不相连的子图,那么称 称之为 的割点或割顶。如果 ,将 删去后, 分裂成两个不相连的子图,则称 为 的桥或割边。
我们可以使用 Tarjan 算法在线性时间内求解无向图的割点和桥。
想要使用 Tarjan 算法,我们需要先了解几个基本概念:
Tarjan 算法
时间戳。我们对图进行深度优先遍历,按照每个节点第一次被访问到的顺序,依次给予 个节点 的整数标记,记为时间戳 ,代表在 DFS 序中出现的位置。
搜索树。在无向连通图中任选一个节点出发进行深度优先遍历,每个点只访问一次,所有发生递归的边 (即 到 是对 的第一次遍历),这样的边有 条,构成一棵树,称之为”无向连通图的搜索树“。如果这张图不连通,那么它会生成若干棵树,称之为”无向图的搜索森林“。
追溯值。除了时间戳外,还有一个概念:追溯值 ,也就是能不经过父亲节点到达的最小时间戳。设 代表搜索树中以 的子树, 定义为以下节点的时间戳的最小值:
- 中的节点;
- 通过 条不在搜索树上的边,可以到达 的节点。
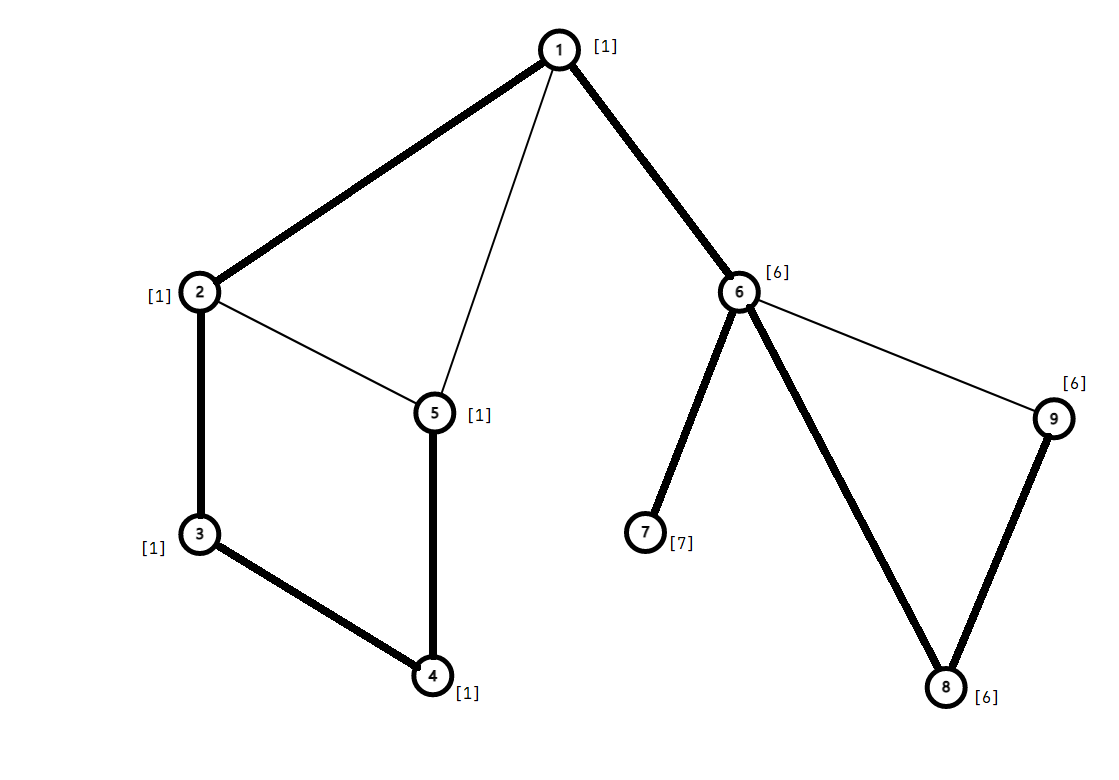
如上图, 节点的追溯值是它自己的时间戳, 一条不在搜索树上的边使得 ,所以 节点都是 的祖先,又因为 这条边,所以 。剩余节点大致同理。
我们计算追溯值时,应该首先令 ,然后考虑 出发的每条边 :如果在搜索树上 是 的父亲,那么 ;如果 不是搜索树上的边,则 。
Tarjan 的时间复杂度为 。
至于追溯值究竟是怎么来的,读者可以自行查阅资料。
割边判定法则
无向边 是割边,当且仅当搜索树上存在一个 的子节点 ,满足 。也就是说从 出发,若不经过 ,怎么走都无法到达 或比 更早访问的节点(因为 ,即想要到 必须经过 ,即 被困在 的子树中了),那么这条边便是桥。
可以发现,桥一定是搜索树中的边,并且一个简单环中的边一定都不是桥。
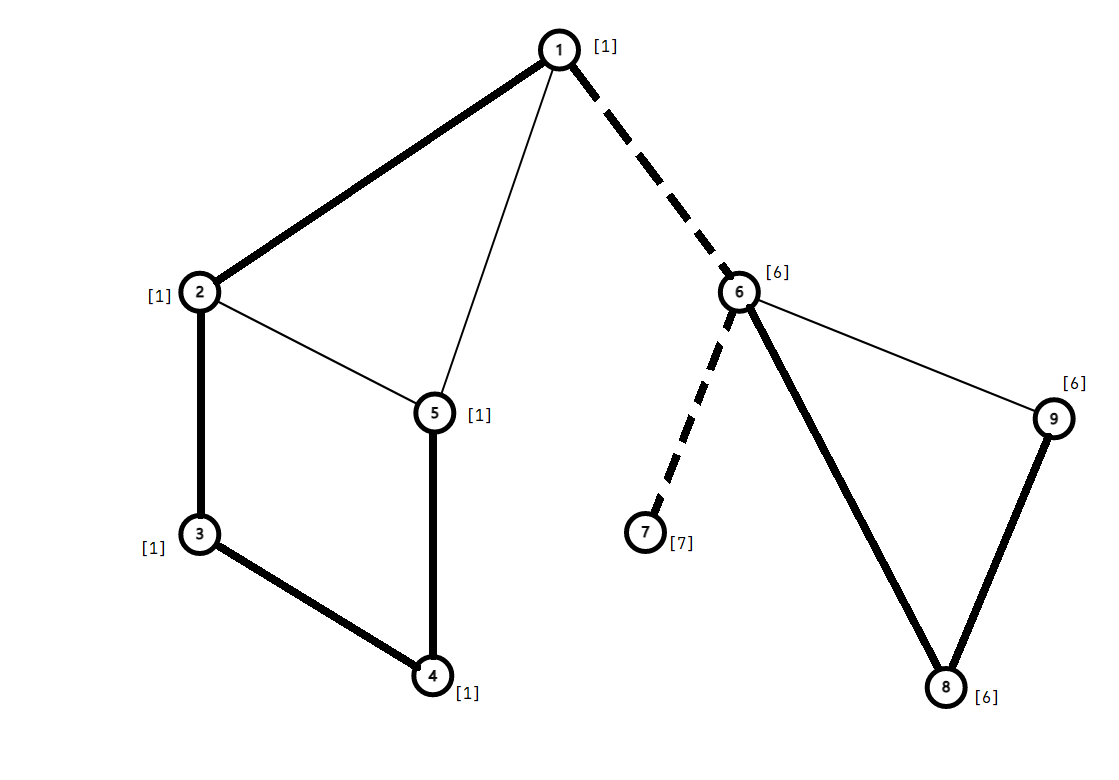
在存边的时候使用了一个 edges 数组,这样使用”成对变换“可以轻松的找到反向边。记录 fa 的话遇到重边时会出错。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, num = 0; // num 用于时间戳的标记
int dfn[105], low[105];
struct edge {
int from, to;
edge(int from = 0, int to = 0) :
from(from), to(to) {}
};
vector <edge> edges;
bool bridge[205];
vector <int> G[105];
inline void addedge(int u, int v) {
edges.push_back(edge(u, v));
G[u].push_back(edges.size() - 1);
}
void tarjan(int x, int in_edge) { // in_edge 记录递归进入 x 的边的编号
dfn[x] = low[x] = ++num; // 标记时间戳,并在初始将 low[x] 标记为 dfn[x]
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].to; // 获取边 (x,y)
if (!dfn[y]) { // 未访问
tarjan(y, G[x][i]); // 递归遍历
// 能跑到这里的肯定是搜索树上的
// 所以 x 是 y 的父亲节点了,也就是 y 属于 subtree(x)
low[x] = min(low[x], low[y]);
// 割边判定法则,在搜索树上存在 x 的一个子节点 y 使得 dfn[x] < low[y]
if (dfn[x] < low[y]) bridge[G[x][i]] = bridge[G[x][i] ^ 1] = true; // 标记的时候标记正边和反边
}
else if (G[x][i] != (in_edge ^ 1)) low[x] = min(low[x], dfn[y]);
// 如果当前这条边是 x->y 的反边 y->x,那么这条命令不会被执行,因为它在搜索树上
// 但是有重边的话他就不是搜索树上的边
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
addedge(u, v), addedge(v, u);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i, -1); // 图不一定连通,每个点都需要 tarjan。最初没有边到 i,用 -1 代替,-1 ^ 1 = -2
puts("Bridges:");
for (int i = 0; i < edges.size(); i += 2)
if (bridge[i]) printf("%d %d\n", edges[i].from, edges[i].to);
return 0;
}割点判定法则
模板。
如果 不是搜索森林中一棵树的根节点,那么 是割点当且仅当搜索树上存在 的子节点 满足 。如果这是根节点,这样的 必须有两个或以上, 才是割点。
由于是小于等于,所以父节点和重边即使不考虑也能得到正确结果。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, root, num = 0, ans = 0;
int dfn[20005], low[20005];
struct edge {
int from, to;
edge(int from = 0, int to = 0) :
from(from), to(to) {}
};
vector <edge> edges;
bool cut[20005];
vector <int> G[20005];
inline void addedge(int u, int v) {
edges.push_back(edge(u, v));
G[u].push_back(edges.size() - 1);
}
void tarjan(int x) {
dfn[x] = low[x] = ++num;
int flag = 0;
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].to;
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (dfn[x] <= low[y]) {
++flag;
if (x != root || flag > 1) cut[x] = true; // 如果不是根节点,或者 flag >= 2,就是割点
}
}
else low[x] = min(low[x], dfn[y]); // 可以直接更新
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
addedge(u, v), addedge(v, u);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) root = i, tarjan(i); // 记录根节点,然后 tarjan
for (int i = 1; i <= n; ++i)
if (cut[i]) ++ans;
printf("%d\n", ans);
for (int i = 1; i <= n; ++i)
if (cut[i]) printf("%d ", i);
putchar('\n');
return 0;
}[POI2008] BLO-Blockade
一张连通的无向图,请你对于每个节点 求出,把与节点 关联的所有边去掉以后(不去掉节点 本身),无向图有多少个有序点对 ,满足 和 不连通。
如果一个点不是割点,那么断掉这个点所连的所有边后图的剩余部分依然连通,只有这个点与图中其它的所有点构成的有序点对满足不连通,共有 个。
如果这个点是割点,那么断掉后图会分裂成若干个连通块。我们应该求出这些连通块的大小,然后两两相乘再将这些积相加。设再搜索树中,节点 的子节点集合中,有 个点满足 ,断掉之后,无向图至多分裂为 个连通块,这些连通块分别是: 个断掉之后的小子树, 个当前节点 自己构成的连通块,图的剩余部分( 的父亲及其它)。
由于 Tarjan 算法本质上是一个 dfs。我们可以使用类似求树的重心的方式,设在搜索树中 表示 的子树大小,那么断掉之后的有序数对数量为:
- 每棵小子树所对应的:
- 当前节点 对应的:
- 剩余部分对应的(前者为剩余部分的大小,后者为小子树和当前节点的大小和):
代码便不难写出:
查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;
struct edge {
int from, to;
edge(int from = 0, int to = 0) :
from(from), to(to) {}
};
int n, m, num;
int dfn[100005], low[100005];
int Size[100005];
i64 ans[100005];
bool cut[100005];
vector <edge> edges;
vector <int> G[100005];
inline void addedge(int u, int v) {
edges.push_back(edge(u, v));
G[u].push_back(edges.size() - 1);
}
void tarjan(int x) {
dfn[x] = low[x] = ++num; Size[x] = 1;
int flag = 0;
i64 sum = 0;
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].to;
if (!dfn[y]) {
tarjan(y);
Size[x] += Size[y];
low[x] = min(low[x], low[y]);
if (dfn[x] <= low[y]) {
++flag;
ans[x] += (i64)Size[y] * (n - Size[y]);
sum += Size[y];
if (x != 1 || flag > 1) cut[x] = true;
}
}
else low[x] = min(low[x], dfn[y]);
}
if (cut[x]) ans[x] += (n - 1) + (n - 1 - sum) * (1 + sum);
else ans[x] = (n - 1) << 1;
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
addedge(u, v); addedge(v, u);
}
tarjan(1); // 所有城市都连通,调用一次 tarjan 即可
for (int i = 1; i <= n; ++i)
printf("%lld\n", ans[i]);
return 0;
}双连通分量与缩点
如果一张图不存在割边,那么这张图被称为边双连通图。如果它不存在割点,那么称之为点双连通图。
接下来给出的两份代码同时也是无向图连通性的模板。
e-DCC 及其缩点
无向连通图的极大边双连通子图被称之为边双连通分量,简记为 e-DCC。其中极大子图的意思是不存在一个更大的子图,这个子图包含了原来的子图,也满足这个限制条件。
一个图的边双连通分量之间一定是不相交的。如果两个双连通分量相交了,那么顺去它们中的一条边,两个子图依然是连通的,也就是说这两个双连通分量是一个更大的双连通分量的一部分。
模板。
e-DCC 的求解非常容易,因为如果图不存在割边,那么我们就把所有的割边都给删掉,图会分裂成若干个连通块,每一个连通块都是一个 e-DCC。
有一个性质:无向连通图是边双连通图,当且仅当任意一条边都包含在至少一个简单环中。
求解 e-DCC 时,经过一个点就要将这个点压入栈。当 时,代表 就是连通块深度最大的点。
查看代码
#include <bits/stdc++.h>
using namespace std;
struct edge {
int from, to;
edge(int from = 0, int to = 0) :
from(from), to(to) {}
};
int n, m, num = 0, cnt = 0, c[500005];
int dfn[500005], low[500005];
bool bridge[4000005];
int st[500005], tot = 0;
vector <edge> edges;
vector <int> G[500005];
vector <int> ans[500005];
inline void addedge(int u, int v) {
edges.push_back(edge(u, v));
G[u].push_back(edges.size() - 1);
}
void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++num;
st[++tot] = x;
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].to;
if (!dfn[y]) {
tarjan(y, G[x][i]);
low[x] = min(low[x], low[y]);
if (dfn[x] < low[y])
bridge[G[x][i]] = bridge[G[x][i] ^ 1] = true;
}
else if (G[x][i] != (in_edge ^ 1)) low[x] = min(low[x], dfn[y]);
}
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--];
ans[cnt].push_back(y);
} while (x != y);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
addedge(u, v), addedge(v, u);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i, -1);
printf("%d\n", cnt);
for (int i = 1; i <= cnt; ++i) {
printf("%d ", ans[i].size());
for (auto x : ans[i])
printf("%d ", x);
putchar('\n');
}
return 0;
}将每一个 e-DCC 都看作一个节点,把割边看作连接 e-DCC 的边,这样会产生一棵树(不连通的无向图就是森林)。这种把 e-DCC 缩为一个节点的方式就叫做缩点,在解决连通性问题的时候非常有用。
for (int i = 0; i < edges.size(); ++i)
if (c[edges[i].from] != c[edges[i].to]) addedge(c[edges[i].from], c[edges[i].to]); // 不在一个 e-DCC 里面,将 e-DCC 连边v-DCC 及其缩点
无向连通图的极大点双连通子图被称之为点双连通分量,简记为 v-DCC。
在求解的时候,每访问到一个新的节点,都需要将它入栈。若割点的判定法则成立,那么无论如何,都要不断弹出节点,直到 被弹出。弹出的所有东西加上 就是一个 v-DCC。还有,如果一个点是自己单独一个,那么它也是一个 v-DCC,需要特判。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, root, num = 0, tot = 0, cnt = 0;
int dfn[500005], low[500005], stack[500005];
vector <int> G[500005], ans[500005];
bool cut[500005];
inline void addedge(int u, int v) { G[u].push_back(v); }
void tarjan(int x) {
dfn[x] = low[x] = ++num;
stack[++tot] = x;
if (x == root && G[x].size() == 0) {
ans[++cnt].push_back(x);
return;
}
int flag = 0;
for (int i = 0; i < G[x].size(); ++i) {
int y = G[x][i];
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
if (dfn[x] <= low[y]) {
++cnt; ++flag;
if (x != root || flag > 1) cut[x] = true;
int z;
do {
z = stack[tot--];
ans[cnt].push_back(z);
} while (z != y);
ans[cnt].push_back(x);
}
}
else low[x] = min(low[x], dfn[y]);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
if (u != v) addedge(u, v), addedge(v, u); // 为了方便判断孤立点,所以自环不能加
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) root = i, tarjan(i);
printf("%d\n", cnt);
for (int i = 1; i <= cnt; ++i) {
printf("%d ", ans[i].size());
for (int j = 0; j < ans[i].size(); ++j)
printf("%d ", ans[i][j]);
putchar('\n');
}
return 0;
}边双连通分量和点双连通分量统称为双连通分量,即 DCC(Double Connected component)。
点双连通分量可以引出圆方树,是解决点相关路径问题的利器,请参看《省选初级图论》。
有向图的连通性
在有向图中,如果任意两个点都可以互相到达,那么这张图被成为强连通图,有向图的极大强连通子图被称之为强连通分量(SCC)。显然,一个点最多属于一个 SCC。
Tarjan 算法
模板.
Tarjan 算法可以求出有向图的强连通分量。当图变成无向图时,该算法也可以正常工作。
这里直接给出代码,原理有时间再写:
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m;
bool ins[10005];
int dfn[10005], low[10005], num = 0;
int st[10005], tot = 0;
int cnt = 0, c[10005], siz[10005];
vector <int> G[10005];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (auto y : G[x])
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
c[y] = cnt; ++siz[cnt];
} while (x != y);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
G[u].emplace_back(v);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i);
int ans = 0;
for (int i = 1; i <= cnt; ++i)
if (siz[i] > 1) ++ans;
printf("%d\n", ans);
return 0;
}缩点
同无向图,将一个 SCC 缩成一个点,便是缩点。有向图在缩点之后可以得到 DAG,然后就可以进行拓扑排序之类的操作。
模板。在做的时候可以发现一个 SCC 内的点都可以到达,缩点之后的权值相当于 SCC 内点的权值综合,而且在 Tarjan 的过程中就可以进行 DP:设 代表从 开始的最大权值,给 SCC 编号时要进行转移,最后也要加上 SCC 内的点权和。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, ans = 0, a[10005], f[10005];
bool ins[10005];
int dfn[10005], low[10005], num = 0;
int st[10005], tot = 0;
int cnt = 0, c[10005], siz[10005];
vector <int> G[10005];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (auto y : G[x])
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y, sum = 0; ++cnt;
do {
y = st[tot--]; ins[y] = false;
c[y] = cnt; ++siz[cnt];
sum += a[y];
for (auto v : G[y])
f[cnt] = max(f[cnt], f[c[v]]);
} while (x != y);
f[cnt] += sum;
ans = max(ans, f[cnt]);
}
}
int main(void) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", a + i);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
G[u].emplace_back(v);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i);
printf("%d\n", ans);
return 0;
}2-SAT 问题
2-SAT 问题。有 个变量,只有 01 两种取值,并有 个需要满足的形如“ 为 或 为 ”(如果给定的是且逻辑也能转化为这种形式),求出一组使得所有条件满足的变量取值(可能无解),。
由于每一个条件只和两个变量相关,可以被构建成图的边。
对于每个变量 ,我们建立两个点, 分别表示 取真假。对于限制条件 ,可以转化为 ,连接这两条边。然后求出这张图的 SCC。
同一 SCC 内的变量值一定相等,那么 就不能在同一个 SCC 内。要满足所有的限制条件,需要 所在的 SCC 的拓扑序在 所在的 SCC 的拓扑序之后才是真,所以要输出 c[i] > c[i+n]。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m;
int dfn[2000005], low[2000005], num;
int st[2000005], tot = 0, col[2000005], cnt = 0;
bool ins[2000005];
vector<int> G[2000005];
void tarjan(int x) {
dfn[x] = low[x] = ++num; ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
col[y] = cnt;
} while (x != y);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, a, v, b; scanf("%d%d%d%d", &u, &a, &v, &b);
G[u + (!a) * n].emplace_back(v + b * n);
G[v + (!b) * n].emplace_back(u + a * n);
}
for (int i = 1; i <= n << 1; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i) if (col[i] == col[i + n]) return puts("IMPOSSIBLE"), 0;
puts("POSSIBLE");
for (int i = 1; i <= n; ++i) printf("%d ", col[i + n] < col[i]);
return putchar('\n'), 0;
}还可以规定一个变量的值。比如规定它为真,那么就从 向 连一条边即可。
欧拉图
从一笔画引出的一类连通性问题。
概述
给定一张图,若存在一条从一个点走到另一个点,不重不漏地经过图上所有的边一次,那么这条路称之为欧拉路。特别地,如果从一个点出发回到了一个点,那么这条路称之为欧拉回路。存在欧拉回路的图称之为欧拉图。不存在欧拉回路但是存在欧拉路的图称为半欧拉图。
在小学已经学过,对于无向图,如果图中度数为奇数的点是 或 ,那么这个图可以一笔画。当为 时,这个图是欧拉图,当为 时,存在欧拉路。
而对于一张有向图(显然,它至少需要弱连通),是欧拉图当且仅当其是一个强连通图且每个节点的入度和出度相等。如果这张图恰存在一个顶点的出度比入度小 ,另一个点入度比出度小 ,这个图存在欧拉路。
Hierholzer 算法
采用 DFS 不断找环,遍历当前节点 的所有出边,如果没有走过那就遍历,遍历完所有出边后将 加入欧拉路径,最后如果遍历的点的个数为 ,那么就得到了反着的欧拉路径,否则欧拉路径不存在。
在找欧拉回路时,可以从任意节点出发。否则,需要从根据性质找到的点出发。
模板,代码入下:
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, in[100005];
vector<int> G[100005];
int tot, st[200005], cur[200005];
void dfs(int x) {
for (; cur[x] < G[x].size(); ) dfs(G[x][cur[x]++]);
st[++tot] = x;
}
int main(void) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
int u, v; scanf("%d%d", &u, &v);
G[u].emplace_back(v); ++in[v];
}
int s = 0;
for (int i = 1; i <= n; ++i) {
sort(G[i].begin(), G[i].end());
if (abs(int(G[i].size()) - in[i]) > 1) return puts("No"), 0;
if (G[i].size() > in[i]) {
if (s) return puts("No"), 0;
else s = i;
}
}
dfs(s ? s : 1);
if (tot != m + 1) return puts("No"), 0;
for (int i = tot; i >= 1; --i) printf("%d ", st[i]);
return putchar('\n'), 0;
}在使用其求无向图的欧拉路径时,需要标记其反向边不可以走了。
哈密顿图
通过图中所有顶点一次的通路称为哈密顿通路,通过图中所有顶点一次的回路称为哈密顿回路。判断一个图是否存在哈密顿回路是 NPC 的,不存在多项式时间复杂度的求法。
其它性质有时间再写。
Problemset
连通性的问题很有意思,我们来看几道题玩一下 。
。
拓扑排序
基础中的基础。
[Luogu P1347] 排序
使用拓扑排序。在过程中记录拓扑序(开一个 ans 数组记录出队的顺序)以便输出答案。矛盾意味着这不是一个 DAG,也就会导致有的点的入度在拓扑排序结束后依然不为 。如果所有的读入都完成后依然没有唯一的拓扑序(通过记录一个点是第几轮入队的,第 轮就是唯一),那么就是有多解。
查看代码
#include <bits/stdc++.h>
#define pii pair<int, int>
#define X first
#define Y second
#define mp make_pair
using namespace std;
int n, m, now, kase = 0;
int inn[30], in[30], ans[30];
bool s[30];
vector <int> G[30];
int topo(void) {
for (int i = 0; i < 26; ++i) in[i] = inn[i];
queue <pii> q;
int sum = 0;
for (int i = 0; i < 26; ++i)
if (s[i] == true && in[i] == 0)
q.push(mp(i, 1));
int res = 0, tot = 0;
while (!q.empty()) {
int u = q.front().X, val = q.front().Y; q.pop();
ans[++tot] = u;
res = max(res, val);
for (int i = 0; i < G[u].size(); ++i) {
int v = G[u][i];
--in[v];
if (in[v] == 0) q.push(mp(v, val + 1));
}
}
if (res == n) return 1;
else {
for (int i = 0; i < 26; ++i)
if (s[i] && in[i] != 0) return 2;
}
return 3;
}
int main(void) {
scanf("%d%d", &n, &m);
char gc[5];
while (m--) {
++kase;
scanf("%s", gc);
G[gc[0] - 'A'].push_back(gc[2] - 'A');
++inn[gc[2] - 'A'];
s[gc[0] - 'A'] = true, s[gc[2] - 'A'] = true;
int t = topo();
if (t == 1) {
printf("Sorted sequence determined after %d relations: ", kase);
for (int i = 1; i <= n; ++i)
printf("%c", ans[i] + 'A');
printf(".\n");
return 0;
}
else if (t == 2) {
printf("Inconsistency found after %d relations.\n", kase);
return 0;
}
}
puts("Sorted sequence cannot be determined.");
return 0;
}[Luogu P1113] 杂务
记 代表完成任务 需要的最短时间。进行拓扑排序,统计一个节点的时候顺带更新它关联的 值。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n;
int len[10005], in[10005], f[10005];
vector <int> G[10005];
void Kahn(void) {
queue <int> q;
for (int i = 1; i <= n; ++i)
if (in[i] == 0) {
q.push(i);
f[i] = len[i];
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int i = 0; i < G[u].size(); ++i) {
--in[G[u][i]];
if (in[G[u][i]] == 0) q.push(G[u][i]);
f[G[u][i]] = max(f[G[u][i]], f[u] + len[G[u][i]]);
}
}
}
int main(void) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int x, y;
scanf("%d%d", &x, len + i);
while (scanf("%d", &y) == 1 && y) {
G[y].push_back(x);
++in[x];
}
}
Kahn();
int ans = 0;
for (int i = 1; i <= n; ++i)
ans = max(ans, f[i]);
printf("%d\n", ans);
return 0;
}[HNOI2015] 菜肴制作
很容易想到拓扑排序,但是这个顺序?我们想要让小的编号尽量靠前,但是直接用小根堆就错了:因为这道题要保证的不是字典序,而是小的尽量靠前,即使一个大的出现在了它前面。这样的话发现一个越大的数,它越在后面越有利,因为这样小的就跑到前面去了。
那么,建反图,进行拓扑排序,使用 Kahn 算法配上一个大根堆,这样可以保证最终大的尽可能地晚出,把小的顶到前面。
本题非常经典,强烈建议读者记住这个结论。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, in[100005], ans[100005];
vector <int> G[100005];
void Kahn(void) {
int tot = 0;
priority_queue <int> q;
for (int i = 1; i <= n; ++i)
if (in[i] == 0) q.push(i);
while (!q.empty()) {
int u = q.top(); q.pop(); ans[++tot] = u;
for (int i = 0; i < G[u].size(); ++i) {
--in[G[u][i]];
if (in[G[u][i]] == 0) q.push(G[u][i]);
}
}
if (tot != n) puts("Impossible!");
else {
for (int i = n; i >= 1; --i)
printf("%d ", ans[i]);
putchar('\n');
}
}
int main(void) {
int T;
scanf("%d", &T);
while (T--) {
memset(in, 0, sizeof(in));
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i) G[i].clear();
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
G[v].push_back(u);
++in[u];
}
Kahn();
}
return 0;
}[CSP-S2020] 函数调用
操作三会导致别的函数调用很多次,而操作二可以看作是它之前的操作重复执行,因此可以考虑一操作执行的次数。对反图进行一次拓扑排序求出乘法标记,然后对正图进行拓扑排序来执行函数。
查看代码
#include <bits/stdc++.h>
using namespace std;
const int P = 998244353;
int n, m, Q;
int a[100005], cnt[100005], in[100005];
vector<int> G[100005], E[100005];
int type[100005], p[100005], v[100005], mul[100005];
void Kahn1(void) { // 在 E 上拓扑排序
queue<int> q;
for (int i = 0; i <= m; ++i) {
in[i] = G[i].size();
if (!in[i]) q.push(i);
}
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : E[u]) {
mul[v] = 1ll * mul[v] * mul[u] % P;
--in[v]; if (!in[v]) q.push(v);
}
}
}
void Kahn2(void) {
queue<int> q;
for (int i = 0; i <= m; ++i) {
in[i] = E[i].size();
if (!in[i]) q.push(i);
}
while (!q.empty()) {
int u = q.front(); q.pop(); int tag = 1;
reverse(G[u].begin(), G[u].end()); // 后调用的函数会让前面的重复执行
for (int v : G[u]) {
cnt[v] = (cnt[v] + 1ll * cnt[u] * tag) % P;
tag = 1ll * tag * mul[v] % P;
--in[v]; if (!in[v]) q.push(v);
}
}
}
int main(void) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", a + i);
scanf("%d", &m); mul[0] = 1;
for (int i = 1; i <= m; ++i) {
scanf("%d", type + i); mul[i] = 1;
if (type[i] == 1) scanf("%d%d", p + i, v + i);
else if (type[i] == 2) scanf("%d", mul + i);
else {
int len; scanf("%d", &len);
while (len--) {
int x; scanf("%d", &x);
G[i].emplace_back(x); E[x].emplace_back(i);
}
}
}
scanf("%d", &Q); cnt[0] = 1;
while (Q--) {
int x; scanf("%d", &x);
G[0].emplace_back(x); E[x].emplace_back(0);
} Kahn1(); Kahn2();
for (int i = 1; i <= n; ++i) a[i] = 1ll * a[i] * mul[0] % P;
for (int i = 1; i <= m; ++i)
if (type[i] == 1) a[p[i]] = (a[p[i]] + 1ll * cnt[i] * v[i]) % P;
for (int i = 1; i <= n; ++i) printf("%d ", a[i]);
putchar('\n'); return 0;
}连通性问题
这里的题都比较基础。
[Luogu P2002] 消息扩散
先求出 SCC,如果两个 SCC 相连,那么只需要发布一个消息就可以了。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m;
int st[100005], tot = 0;
bool ins[100005];
int dfn[100005], low[100005], num = 0;
int cnt = 0, c[100005];
vector<int> G[100005];
bool flag[100005];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
c[y] = cnt;
} while (x != y);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
G[u].push_back(v);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i)
for (int j : G[i])
if (c[i] != c[j]) flag[c[j]] = true;
int ans = 0;
for (int i = 1; i <= cnt; ++i)
ans += (flag[i] == 0);
printf("%d\n", ans);
return 0;
}[USACO03FALL] 受欢迎的牛 G
只有当出度为 的 SCC 仅有一个时,才会有明星出现,数量是这个 SCC 的大小。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m;
int st[10005], tot = 0;
bool ins[10005];
int out[10005];
int c[10005], siz[10005], cnt = 0;
int dfn[10005], low[10005], num = 0;
vector <int> G[10005];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
siz[cnt] += 1; c[y] = cnt;
} while (x != y);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
G[u].emplace_back(v);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i)
for (int j : G[i])
if (c[i] != c[j]) ++out[c[i]];
int ans = 0, flag = 0;
for (int i = 1; i <= cnt; ++i)
if (out[i] == 0) ans = siz[i], ++flag;
if (flag > 1) puts("0");
else printf("%d\n", ans);
return 0;
}[USACO5.3] Network of Schools
第二问的答案是缩点之后入度为 的点的个数和出度为 的点的个数的最大值。特别地,当只有一个 SCC 时,答案为 。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n;
int st[10005], tot = 0;
bool ins[10005];
int dfn[10005], low[10005], num = 0;
int cnt = 0, c[10005];
vector <int> G[10005];
bool flag[10005];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
c[y] = cnt;
} while (x != y);
}
}
int in[10005], out[10005];
int main(void) {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int j;
while (scanf("%d", &j) == 1 && j) G[i].push_back(j);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i)
for (int j : G[i])
if (c[i] != c[j]) {
flag[c[j]] = true;
++in[c[j]], ++out[c[i]];
}
int ans = 0, p = 0, q = 0;
for (int i = 1; i <= cnt; ++i) {
ans += (flag[i] == 0);
p += (in[i] == 0);
q += (out[i] == 0);
}
printf("%d\n%d\n", ans, cnt == 1 ? 0 : max(p, q));
return 0;
}[APIO2009] 抢掠计划
显然是缩点后进行 DP,不过这里显然用以 为终点的状态比较方便,所以 Tarjan 之后要重新建图。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, s, p;
int low[500005], dfn[500005], num = 0;
int st[500005], tot = 0, f[500005];
int val[500005], sum[500005], c[500005], cnt = 0;
bool ins[500005];
vector<int> G[500005];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) { tarjan(y); low[x] = min(low[x], low[y]); }
else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
c[y] = cnt; sum[cnt] += val[y];
} while (x != y);
}
}
int in[500005];
vector<int> G2[500005];
int main(void)
{
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
G[u].emplace_back(v);
}
for (int i = 1; i <= n; ++i) scanf("%d", val + i);
scanf("%d%d", &s, &p);
tarjan(s);
for (int i = 1; i <= n; ++i)
if (c[i]) for (int j : G[i])
if (c[i] != c[j]) {
G2[c[i]].push_back(c[j]);
++in[c[j]];
}
queue<int> q;
q.push(c[s]); f[c[s]] = sum[c[s]];
while (!q.empty()) {
int u = q.front(); q.pop();
for (int v : G2[u]) {
f[v] = max(f[v], f[u] + sum[v]);
--in[v];
if (in[v] == 0) q.push(v);
}
}
int ans = 0;
for (int i = 1; i <= p; ++i) {
int x;
scanf("%d", &x);
ans = max(ans, f[c[x]]);
}
printf("%d\n", ans);
return 0;
}[Luogu P2656] 采蘑菇
显然一个 SCC 内的蘑菇可以采干净,那么 SCC 缩点之后在 DAG 上 DP 即可。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, s;
int dfn[80005], low[80005], num = 0;
int st[80005], tot = 0;
bool ins[80005];
int cnt, c[80005];
vector<int> G[80005];
struct edge {
int u, v, w; long double d;
edge(int u = 0, int v = 0, int w = 0, long double d = 0) :
u(u), v(v), w(w), d(d) {}
};
vector<edge> edges;
inline void addedge(int u, int v, int w, long double d) {
edges.emplace_back(edge(u, v, w, d));
G[u].emplace_back(edges.size() - 1);
}
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].v;
if (!dfn[y]) { tarjan(y); low[x] = min(low[x], low[y]); }
else if (ins[y]) low[x] = min(low[x], dfn[y]);
}
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
c[y] = cnt;
} while (x != y);
}
}
int val[80005], in[80005], f[80005], ans = 0;
vector<edge> G2[80005];
void Kahn(void) {
queue<int> q;
q.push(c[s]);
while (!q.empty()) {
int u = q.front(); q.pop(); f[u] += val[u];
for (int i = 0; i < G2[u].size(); ++i) {
edge &e = G2[u][i];
f[e.v] = max(f[e.v], f[u] + e.w);
--in[e.v];
if (in[e.v] == 0) q.push(e.v);
}
ans = max(ans, f[u]);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v, w; long double d;
scanf("%d%d%d%Lf", &u, &v, &w, &d);
addedge(u, v, w, d);
}
scanf("%d", &s); tarjan(s);
for (int i = 0; i < edges.size(); ++i) {
edge &e = edges[i];
if (dfn[e.u] && dfn[e.v]) {
if (c[e.u] == c[e.v]) {
while (e.w) {
val[c[e.u]] += e.w;
e.w *= e.d;
}
}
else {
G2[c[e.u]].push_back(edge(c[e.u], c[e.v], e.w, e.d));
++in[c[e.v]];
}
}
}
Kahn();
printf("%d\n", ans);
return 0;
}[USACO06JAN] Redundant Paths G
直接求出 e-DCC 缩点后的树,然后将叶子配对即可。
查看代码
#include <bits/stdc++.h>
using namespace std;
struct edge {
int from, to;
edge(int from = 0, int to = 0) :
from(from), to(to) {}
};
int n, m, num = 0, cnt = 0;
int dfn[5005], low[5005], c[5005], in[5005];
bool bridge[20005];
vector <edge> edges;
vector <int> G[5005];
inline void addedge(int u, int v) {
edges.push_back(edge(u, v));
G[u].push_back(edges.size() - 1);
}
void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++num;
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].to;
if (!dfn[y]) {
tarjan(y, G[x][i]);
low[x] = min(low[x], low[y]);
if (dfn[x] < low[y]) bridge[G[x][i]] = bridge[G[x][i] ^ 1] = true;
}
else if (G[x][i] != (in_edge ^ 1)) low[x] = min(low[x], dfn[y]);
}
}
void dfs(int x) {
c[x] = cnt;
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].to;
if (c[y] || bridge[G[x][i]]) continue;
dfs(y);
}
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
addedge(u, v), addedge(v, u);
}
tarjan(1, -1);
int res = 0;
for (int i = 1; i <= n; ++i)
if (!c[i]) {
++cnt;
dfs(i);
}
for (int i = 0; i < edges.size(); i += 2) // 统计叶子的个数,入度为 1 的是叶子
if (c[edges[i].from] != c[edges[i].to]) {
++in[c[edges[i].from]];
++in[c[edges[i].to]];
}
int ans = 0;
for (int i = 1; i <= n; ++i)
if (in[i] == 1) ++ans;
printf("%d\n", (ans + 1) / 2);
return 0;
}连通性的应用
这里的题都需要一些简单分析能力。
[CF1777E] Edge Reverse
显然是二分答案,可以反转的边相当于无向边,将图 SCC 缩点后应该恰好有一个入度为 的点才能满足条件。
查看代码
#include <bits/stdc++.h>
using namespace std;
struct edge {
int u, v, w;
bool operator < (const edge &a) const {
return w < a.w;
}
} e[200005];
int n, m;
vector<int> G[200005];
int dfn[200005], low[200005], num, st[200005], tot;
int cnt, col[200005], deg[200005];
bool ins[200005];
void tarjan(int x) {
dfn[x] = low[x] = ++num; ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (dfn[x] == low[x]) {
int y; ++cnt;
do ins[y = st[tot--]] = false, col[y] = cnt; while (x != y);
}
}
bool P(int x) {
for (int i = 1; i <= n; ++i) G[i].clear(), dfn[i] = ins[i] = deg[i] = 0;
for (int i = 1; i <= m; ++i) {
G[e[i].u].emplace_back(e[i].v);
if (i <= x) G[e[i].v].emplace_back(e[i].u);
} num = tot = cnt = 0;
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
for (int u = 1; u <= n; ++u) for (int v : G[u]) if (col[u] != col[v]) ++deg[col[v]];
int res = 0;
for (int i = 1; i <= cnt; ++i) res += (deg[i] == 0);
return res == 1;
}
int main(void) {
int T; scanf("%d", &T); while (T--) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) scanf("%d%d%d", &e[i].u, &e[i].v, &e[i].w);
sort(e + 1, e + m + 1);
int L = -1, R = m + 1;
while (L + 1 != R) {
int mid = L + R >> 1;
if (P(mid)) R = mid;
else L = mid;
}
printf("%d\n", R != m + 1 ? e[R].w : -1);
}
return 0;
}[NOI2017] 游戏
我们只要枚举 是 还是 ,就可以覆盖所有选择的地图,这样就是一个 2-SAT 模板。时间复杂度为 。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, d; char s[50005];
int dfn[100005], low[100005], num, st[100005], tot;
bool ins[100005], flag;
vector<int> G[100005];
int col[100005], cnt;
void tarjan(int x) {
dfn[x] = low[x] = ++num; ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) tarjan(y), low[x] = min(low[x], low[y]);
else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
++cnt; int y;
do ins[y = st[tot--]] = false, col[y] = cnt; while (x != y);
}
}
int a[100005], b[100005]; char x[100005], y[100005];
int pos[10]; char val[10]; bool c[3][3]; // 当不允许使用 i 时,使用了 i+1 为真,否则为假
bool solve(void) {
num = tot = cnt = 0;
for (int i = 1; i <= n << 1; ++i) dfn[i] = ins[i] = 0, G[i].clear();
for (int i = 1; i <= d; ++i) s[pos[i]] = val[i];
for (int i = 1; i <= m; ++i) {
if (s[a[i]] == x[i]) continue;
bool p = c[s[a[i]] - 'A'][x[i] - 'A'], q = c[s[b[i]] - 'A'][y[i] - 'A'];
if (s[b[i]] == y[i]) {
G[a[i] + (!p) * n].emplace_back(a[i] + p * n); // 此时不能满足 a 自己的限制条件,必须让其为假
continue;
}
G[a[i] + (!p) * n].emplace_back(b[i] + (!q) * n);
G[b[i] + q * n].emplace_back(a[i] + p * n);
}
for (int i = 1; i <= n << 1; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i) if (col[i] == col[i + n]) return 0;
for (int i = 1; i <= n; ++i) putchar((s[i] - 'A' + (col[i + n] > col[i] ? 1 : 2)) % 3 + 'A');
return putchar('\n'), 1;
}
void dfs(int x) {
if (flag) return; if (x > d) return flag = solve(), void();
val[x] = 'A'; dfs(x + 1); val[x] = 'B'; dfs(x + 1);
}
int main(void) {
scanf("%d%d%s%d", &n, &d, s + 1, &m); d = 0; c[0][1] = c[1][2] = c[2][0] = 1;
for (int i = 1; i <= n; ++i) { s[i] -= 32; if (s[i] == 'X') pos[++d] = i; }
for (int i = 1; i <= m; ++i) scanf("%d %c %d %c", a + i, x + i, b + i, y + i);
dfs(1); if (!flag) puts("-1"); return 0;
}[yLOI2018] 锦鲤抄
先考虑一个 DAG 的情况。我们只要先找到需要删除的点(能够被删除且是前 大),然后按照这些点的拓扑序的倒序删点,那么可以发现这些点都可以被删去,并不会影响后面的点的入度。
因此对原图进行 SCC 缩点,这样整体上的逻辑是不变的,我们只需要单独考虑一下 SCC 内部怎么删。看一个简单的:

现在 在一个 SCC 内,由于这个 SCC 是有一个入度的 ,因此只要不先删 ,那么这个 SCC 就可以删干净。但是如果没有 这条边呢?那么 SCC 删完必须留一个点(只需要从任意一个位置开始顺着环删,最后就会剩一个点),但是!如果这个 SCC 内存在自环,那么它还是可以被删干净的。
因此我们只需要排除掉本来就入度为 的点和一个没有入度没有自环的 SCC 内的点权最小的点,剩下的点取前 大即可。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, k;
int w[500010];
int dfn[500010], low[500010], num = 0;
int st[500010], tot = 0;
int cnt = 0, c[500010];
bool ins[500010];
vector<int> G[500010];
vector<int> scc[500010];
bool self[500010];
bool selfscc[500010];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
ins[st[++tot] = x] = true;
for (int y : G[x])
if (!dfn[y]) {
tarjan(y);
low[x] = min(low[x], low[y]);
} else if (ins[y]) low[x] = min(low[x], dfn[y]);
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--]; ins[y] = false;
c[y] = cnt; scc[cnt].push_back(y);
selfscc[cnt] |= self[y];
} while (x != y);
}
}
int in[500010];
int val[500010], tot2 = 0;
int main(void) {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= n; ++i) scanf("%d", w + i);
while (m--) {
int u, v; scanf("%d%d", &u, &v);
if (u != v) G[u].push_back(v);
else self[u] = true;
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; ++i)
for (int j : G[i]) if (c[i] != c[j]) ++in[c[j]];
for (int i = 1; i <= cnt; ++i) {
int minn = 1e9, flag = false;
for (int j : scc[i]) minn = min(minn, w[j]);
for (int j : scc[i])
if (in[i] || selfscc[i]) val[++tot2] = w[j];
else if (w[j] > minn || flag) val[++tot2] = w[j];
else flag = true;
}
sort(val + 1, val + tot2 + 1, greater<int>());
int ans = 0;
for (int i = 1; i <= k; ++i) ans += val[i];
printf("%d\n", ans);
return 0;
}[CF51F] Caterpillar
一个毛毛虫定义为一个无向联通无环图上存在一条路径 使得任意一个节点距离 的距离至多为 。
毛毛虫可以包含自环(一条从一个顶点连向自己的边),但是不可以包含重边。
这个图片是一个毛毛虫的例子:
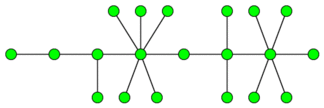
现在你有一张无向图 (不一定联通) 。你被允许做一些合并操作。
每次操作将两个顶点合并成一个顶点。每次选择任意两个顶点 ,这些顶点以及它们的边(至少连接着 中一个点的边)将被删除,而后顶点 会被加入,以及对于每条边 都会有新边 加入。如果有一条边 它会被转换成自环 。得到的图(操作结束后)可能会有重边。我们注意到这个操作减少了 个顶点,却没有改变边的数量。
合并操作可以简单的描述为将图中两个顶点合并为图中的一个顶点并继承原来所有的边。你可以连续地使用合并操作,从而将给定的图转变成一个毛毛虫。求出这张图转变成一个毛毛虫的最少操作次数。
毛毛虫上不能长出来环,所以把每一个 e-DCC 缩点,图会变成一个森林,我们需要处理每一棵树,然后把这些树合并,需要树的个数减去一的代价。
由于环必须要合并,如果要直接统计操作次数还需要统计环的大小,不妨换一个思路,默认所有点都需要合并,然后减去不需要合并的。
现在考虑最后一个问题,一棵树怎么处理?直觉告诉我们:这条路径 应该是长度为 直径,这样才能让要动的点更少。直径可以让我们少合并 个点,叶子上的点也可以不用合并(画个图看看),但是直径两端还有两个叶子,所以要减去。
查看代码
#include <bits/stdc++.h>
using namespace std;
struct edge {
int u, v;
edge(int u = 0, int v = 0) :
u(u), v(v) {}
};
int n, m, cnt = 0, ans = 0, c[50005];
int num = 0, dfn[50005], low[50005];
int st[50005], tot = 0;
bool vis[50005];
vector <int> G[50005], F[50005];
vector <edge> edges;
inline void addedge(int u, int v) {
edges.push_back(edge(u, v));
G[u].push_back(edges.size() - 1);
}
void tarjan(int x, int in_edge) {
dfn[x] = low[x] = ++num;
st[++tot] = x;
for (int i = 0; i < G[x].size(); ++i) {
int y = edges[G[x][i]].v;
if (!dfn[y]) {
tarjan(y, G[x][i]);
low[x] = min(low[x], low[y]);
} else if (G[x][i] != (in_edge ^ 1)) low[x] = min(low[x], dfn[y]);
}
if (low[x] == dfn[x]) {
int y; ++cnt;
do {
y = st[tot--];
c[y] = cnt;
} while (x != y);
}
}
vector <int> li;
int d[50005];
void dfs(int x, int fa) {
d[x] = d[fa] + 1;
for (int y : F[x])
if (y != fa) dfs(y, x);
}
void find(int x) {
li.emplace_back(x); vis[x] = true;
for (int i : F[x]) if (!vis[i]) find(i);
}
void kill(int x) {
if (F[x].empty()) return ans += 1, void();
li.clear(); find(x);
dfs(x, 0);
int u = x, leaf = 0;
for (int y : li) if (d[y] > d[u]) u = y;
d[u] = 0; dfs(u, 0);
for (int y : li) if (d[y] > d[u]) u = y;
for (int y : li) leaf += (F[y].size() == 1);
ans += d[u] + leaf - 2;
}
int main(void) {
scanf("%d%d", &n, &m);
while (m--) {
int u, v;
scanf("%d%d", &u, &v);
addedge(u, v);
addedge(v, u);
}
for (int i = 1; i <= n; ++i)
if (!dfn[i]) tarjan(i, -1);
for (int i = 0; i < edges.size(); ++i)
if (c[edges[i].u] != c[edges[i].v]) F[c[edges[i].u]].push_back(c[edges[i].v]);
int ret = -1;
for (int i = 1; i <= n; ++i)
if (!vis[i]) ++ret, kill(i);
printf("%d\n", n - ans + ret);
return 0;
}欧拉路问题
与欧拉路径相关的问题。
[Luogu P1341] 无序字母对
模板,找无向图的一笔画。
查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int H(char x) {
if (x >= 'A' && x <= 'Z') return x - 'A' + 1;
return x - 'a' + 27;
}
char V(int x) {
if (x <= 26) return x - 1 + 'A';
return x - 27 + 'a';
}
int m, G[60][60], tot, in[60];
char st[1005];
void dfs(int x) {
for (int i = 1; i <= 52; ++i) if (G[x][i]) {
G[x][i] = G[i][x] = false;
dfs(i);
}
st[++tot] = V(x);
}
int main(void) {
scanf("%d", &m); int sta = 1e9;
for (int i = 1; i <= m; ++i) {
char s[5]; scanf("%s", s);
int u = H(s[0]), v = H(s[1]);
G[u][v] = G[v][u] = 1; ++in[u]; ++in[v];
sta = min({sta, u, v});
}
int cnt = 0, h = 0;
for (int i = 1; i <= 52; ++i) if (in[i] & 1) {
++cnt;
if (!h) h = i;
}
if (cnt == 1 || cnt > 2) return puts("No Solution"), 0;
dfs(h ? h : sta);
if (tot != m + 1) return puts("No Solution"), 0;
for (int i = tot; i >= 1; --i) putchar(st[i]);
return putchar('\n'), 0;
}[CF1152E] Neko and Flashback
对于一个 ,有 ,也就是说 各是 其中的一个(当然需要 ,否则无解)。 注意这个输出方式, 的作用是将 排列,也就是说我们只需要求出 有哪些数组成即可。将给定的 的关系看成一条无向边,走过这个路径就相当于满足了一个限制条件。那么在图上找出欧拉路,就可以得到一个满足所有的限制条件的序列 (需要先离散化后再建图)。时间复杂度 。
查看代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
int n, tot, cur[100005], deg[200005], st[200005];
int b[100005], c[100005], B[200005];
vector<int> edges;
vector<int> G[200005];
inline void addedge(int u, int v) {
edges.emplace_back(v); G[u].emplace_back(edges.size() - 1);
++deg[v];
}
void dfs(int x) {
for (; cur[x] < G[x].size(); ++cur[x]) {
int y = edges[G[x][cur[x]]];
if (y) {
edges[G[x][cur[x]]] = 0, edges[G[x][cur[x]] ^ 1] = 0;
dfs(y);
}
}
st[++tot] = x;
}
int main(void) {
scanf("%d", &n);
for (int i = 1; i < n; ++i) scanf("%d", b + i), B[++tot] = b[i];
for (int i = 1; i < n; ++i) scanf("%d", c + i), B[++tot] = c[i];
sort(B + 1, B + tot + 1); tot = unique(B + 1, B + tot + 1) - (B + 1);
for (int i = 1; i < n; ++i) {
b[i] = lower_bound(B + 1, B + tot + 1, b[i]) - B;
c[i] = lower_bound(B + 1, B + tot + 1, c[i]) - B;
if (b[i] > c[i]) return puts("-1"), 0;
addedge(b[i], c[i]); addedge(c[i], b[i]);
}
int cnt = 0, h = 0;
for (int i = 1; i <= tot; ++i) if (deg[i] & 1) {
++cnt;
if (!h) h = i;
}
if (cnt == 1 || cnt > 2) return puts("-1"), 0;
tot = 0; dfs(h ? h : 1);
if (tot != n) return puts("-1"), 0;
for (int i = tot; i >= 1; --i) printf("%d ", B[st[i]]);
putchar('\n');
return 0;
}[CF36E] Two Paths
一道值得一想不值得一写的欧拉路。
原图中最多只能有两个连通块,有两个时就是分别找欧拉路,下面来看只有一个。
如果它只有零个或两个奇点,那么有一个欧拉路,我们把这条路径分开一条边作为一部分,这样就是两部分了(分不出来就无解)!
如果有四个奇点,那么是两个(半)欧拉图拼起来的,因此考虑给两个奇点连一条假边,跑欧拉路,输出的时候以这条假边为分界输出两部分。
由于要输出边的编号,因此用链式前向星方便一些,搞点的时候遍历所有的边寻找对应的是哪一条。
查看代码
#include <bits/stdc++.h>
using namespace std;
int n, m, edgecnt = 1, dcc, oddcnt, head[10005], d[10005];
int dccOdd[10005], v[10005], U[10005], V[10005], b[20005];
bool vis[10005], printed[10005];
vector<int> ans;
struct Edge {
int to, nxt;
} G[20005];
inline void addedge(int u, int v) {
G[++edgecnt] = {v, head[u]};
head[u] = edgecnt; ++d[v];
}
void mark(int x) {
v[x] = dcc; dccOdd[dcc] += d[x] & 1; oddcnt += d[x] & 1;
for (int i = head[x], y; i; i = G[i].nxt)
if (!v[y = G[i].to]) mark(y);
}
void dfs(int u) {
if (!d[u]) return ans.emplace_back(u), void();
for (int i = head[u], v; i; i = G[i].nxt)
if (!vis[i >> 1]) {
vis[i >> 1] = true, --d[v = G[i].to], --d[u];
dfs(v);
}
ans.emplace_back(u);
}
void print(int l, int r) {
for (int i = l; i < r; ++i)
for (int j = head[ans[i]]; j; j = G[j].nxt)
if (!printed[j >> 1] && j >> 1 <= m && ans[i + 1] == G[j].to) {
if (i != l) putchar(' ');
printed[j >> 1] = true;
printf("%d", j >> 1);
break;
}
putchar('\n');
}
int main(void) {
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
scanf("%d", &m);
for (int i = 1; i <= m; ++i) {
scanf("%d%d", U + i, V + i);
b[i << 1] = U[i]; b[(i << 1) - 1] = V[i];
}
sort(b + 1, b + 2 * m + 1); n = unique(b + 1, b + 2 * m + 1) - (b + 1);
for (int i = 1; i <= m; ++i) {
U[i] = lower_bound(b + 1, b + n + 1, U[i]) - b;
V[i] = lower_bound(b + 1, b + n + 1, V[i]) - b;
addedge(U[i], V[i]); addedge(V[i], U[i]);
}
for (int i = 1; i <= n; ++i) if (!v[i]) ++dcc, mark(i);
if (oddcnt > 4 || dcc > 2) return puts("-1"), 0;
if (dcc == 1) {
int ond1 = 0, ond2 = 0, st = 0;
if (oddcnt == 0) dfs(1);
else if (oddcnt == 2) {
for (int i = 1; i <= n; ++i)
if (d[i] & 1) { dfs(i); break; }
} else {
for (int i = 1; i <= n && !st; ++i)
if (d[i] & 1) {
if (!ond1) ond1 = i;
else if (!ond2) ond2 = i;
else st = i;
}
addedge(ond1, ond2), addedge(ond2, ond1); // 两个奇数点加一条虚拟边
++d[ond1], ++d[ond2]; dfs(st);
}
if (oddcnt != 4) {
if (ans.size() <= 2) return puts("-1"), 0;
printf("%d\n", 1); print(0, 1);
printf("%d\n", ans.size() - 2); print(1, ans.size());
} else {
int _pre = 0;
for (int i = 0; i < ans.size(); ++i) {
if ((_pre == ond1 && ans[i] == ond2) || (_pre == ond2 && ans[i] == ond1)) {
printf("%d\n", i - 1); print(0, i - 1);
printf("%d\n", m - i + 1); print(i, ans.size());
break;
}
_pre = ans[i];
}
}
} else {
if (dccOdd[1] > 2 || dccOdd[2] > 2) return puts("-1"), 0;
int nowVis = 0;
for (int i = 1; i <= n; ++i)
if ((!nowVis || v[i] != nowVis) && bool(dccOdd[v[i]]) == (d[i] & 1)) {
dfs(i);
printf("%d\n", ans.size() - 1); print(0, ans.size());
ans.clear(); if (nowVis) break; nowVis = v[i];
}
}
return 0;
}

