NOI 一轮复习 II：数据结构 A

本文是 NOI 一轮复习的第二篇，包括各类常用数据结构。

树状数组

又称 Fenwick 树、二叉索引树（BIT）。支持维护前缀后缀的信息。

概述

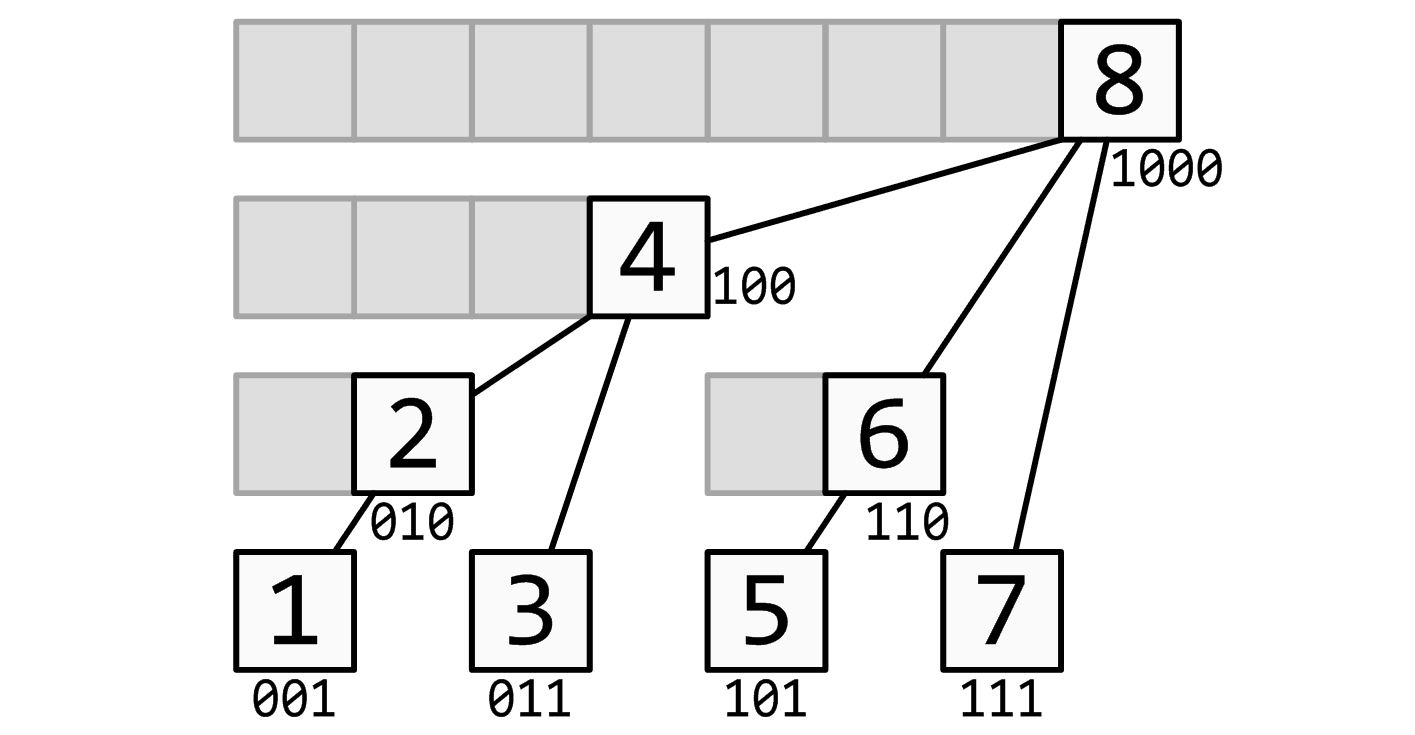
树状数组将序列拆分成了恰好 $n$ 个区间，对于每一个前缀求解都可以拆成 $\log p$ 个区间进行求解，而且自带一个卡不掉的 $1/2$ 的常数，随机数据下则为 $1/4$ 的常数！我们通过 $\operatorname{lowbit}$ 来支持树状数组的工作。

一个显式的树状数组

模板，区间和我们可以用前缀和相减来求解，代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 

int n, m; 
int a[500005]; i64 C[500005]; 

void add(int x, int k) { for (; x <= n; x += x & -x) C[x] += k; }
i64 sum(int x) { i64 r = 0; for (; x; x -= x & -x) r += C[x]; return r; }

int main(void) {
    scanf("%d%d", &n, &m); 
    for (int i = 1; i <= n; ++i) scanf("%d", a + i), add(i, a[i]); 
    while (m--) {
        int op, x, y; scanf("%d%d%d", &op, &x, &y); 
        if (op == 1) add(x, y); 
        else printf("%lld\n", sum(y) - sum(x - 1)); 
    }
    return 0;
}

树状数组自身也有许多漂亮的操作，虽然效率上略微胜于线段树和平衡树，但是可扩展性和直观程度上却不如它们。下面我们来看一些必须掌握的。

线性建树

对于树状数组上的每个节点都向上传递，具体过程如下：

for (int i = 1; i <= n; ++i) {
    int x; cin >> x; C[i] += x; 
    if (i + lowbit(i) <= n) C[i + lowbit(i)] += C[i]; 
}

差分与前缀和

树状数组可以轻松维护序列的高阶前缀和，首先将原序列差分可以直接解决区间加单点查询。

将原序列前缀和：

可以得到 $b_{k,i}=b_{k,i-1}+b_{k-1,i}$。这是网格图路径计数，也就是说，$b_{k,i}=\dbinom {i+k-1}{k-1}$。

也就是说，我们要求：

$$\sum_{i=1}^x \binom{x+k-1-i} {k-1} a_i$$

由范德蒙德卷积得：

$$\sum_{i=1}^x \sum_{j=0}^{k-1} \binom x j \binom{k-1-i}{k-1-j} a_i$$

分离，可得：

$$\sum_{j=0}^{k-1} \binom x j \sum_{i=1}^x \binom{k-1-i}{k-1-j} a_i$$

后面那一坨可以使用树状数组维护，前面直接乘就行。注意这里的是广义二项式系数，也就是说：

$$\binom n m =\frac {\prod_{i=n-m+1}^{n}i}{m!}$$

模板，代码如下：

int C(int n, int m) {
    if (n < 0) return 1ll * fac[m - n - 1] * ifac[-n - 1] % P * ifac[m] % P * (m & 1 ? P - 1 : 1) % P; 
    if (n < m) return 0; 
    return 1ll * fac[n] * ifac[m] % P * ifac[n - m] % P; 
}
void add(int p, int x, int y) {
    for (int i = x; i <= n; i += i & -i)
        a[p][i] = (a[p][i] + 1ll * C(k - x, k - p) * y % P) % P; 
}
int sum(int p, int x) {
    int r = 0; 
    for (int i = x; i; i -= i & -i) r = (r + a[p][i]) % P; 
    return r; 
}

main() {
    scanf("%d%d%d", &n, &k, &m); --k; 
    for (int i = 1; i <= n; ++i) {
        int x; scanf("%d", &x); 
        for (int j = 0; j <= k; ++j) add(j, i, x); 
    }
    while (m--) {
        int op, x; scanf("%d%d", &op, &x); 
        if (op == 1) {
            int y; scanf("%d", &y); 
            for (int i = 0; i <= k; ++i) add(i, x, y); 
        } else {
            int ans = 0; 
            for (int i = 0; i <= k; ++i)
                ans = (ans + 1ll * C(x, i) * sum(i, x) % P) % P;
            printf("%d\n", (ans + P) % P);  
        }
    }
}

当 $k$ 较小时，也可以手推结论：对于 $k$ 阶前缀和，写出 $\dbinom{y-x+k-1}{k-1}$ 的多项式形式，然后 $y$ 表示的是下标，$x$ 表示的是当前位置的值。

比如 $k=3$ 时：

$$\dbinom{y-x+2}{2}=\frac{(y-x+2)(y-x+1)}{2}$$

所以展开为：

$$\frac{x^2-(2y-3)x^1+(y^2+3y+2)x^0}{2}$$

那么维护 $vx^i$ 在 $y$ 处的前缀和，统计答案即可。这样的好处是不用写广义二项式系数来计算贡献。

考虑枚举每个种类的数分别计算，设当前选中的数为 $w$，$S_i$ 为前 $i$ 个数中 $w$ 的个数。

对于一段区间 $[l+1,r]$（方便差分），满足条件时有 $S_r-S_l>r-l-(S_r-S_l)\rightarrow 2S_r-r>2S_l-l$，也就是在求 $P_i=2S_i-i$ 的逆序对个数。

对于同一个 $w$，$P_i$ 可以划分成若干个单调递减区间，总数在 $O(n)$ 级别。同一个区间内是没有贡献的，只需要计算 $l$ 在前面区间内的贡献。

设 $c_i$ 代表 $i$ 在 $P$ 中的出现次数（由于可能有负的，所以需要加上一个偏移量），$T$ 表示 $c_i$ 的前缀和，那么每一个 $P_i$ 的贡献就是当前的 $T_{P_i-1}$。对于一段 $[x,y]$，总贡献就是 $\sum\limits_{i=x-1}^{y-1}T_i$，再求一个 $T$ 的前缀和 $G$ 即可。

这玩意就是三阶前缀和。

int n, type;
int a[500005];
vector<int> b[500005]; 

i64 C1[1000005], C2[1000005], C3[1000005]; 
i64 sum(int x) {
    i64 res = 0; 
    for (int i = x; i > 0; i -= i & -i) 
        res += C1[i] * (x + 2) * (x + 1) - C2[i] * (2 * x + 3) + C3[i];
    return res;
}
void add(int x, i64 k) {
    for (int i = x; i <= 2 * n + 1; i += i & -i) 
        C1[i] += k, C2[i] += k * x, C3[i] += k * x * x;
}

int main(void) {
    scanf("%d%d", &n, &type);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i), b[a[i]].emplace_back(i);
    i64 ans = 0; const int N = n + 1; 
    for (int i = 0; i < n; ++i) {
        b[i].emplace_back(n + 1); int last = 0;
        for (int j = 0; j < b[i].size(); ++j) {
            int x = 2 * j - b[i][j] + 1 + N, y = 2 * j - last + N;  
            ans += sum(y - 1) - sum(x - 2); 
            add(x, 1); add(y + 1, -1);
            last = b[i][j];
        }
        last = 0; 
        for (int j = 0; j < b[i].size(); ++j) {
            int x = 2 * j - b[i][j] + 1 + N, y = 2 * j - last + N; 
            add(x, -1); add(y + 1, 1);
            last = b[i][j]; 
        }
    }
    return !printf("%lld\n", ans / 2); 
}

树状数组二分与倍增

我们当然可以使用二分套树状数组达到 $O(n\log^2 n)$ 的复杂度，然而有没有更好的方式适配树状数组这种结构呢？有！倍增！

查询一个权值树状数组里的 $k$ 小值。

我们从二进制高位到低位枚举，时间复杂度为 $O(n\log n)$。

// 权值树状数组查询第 k 小
int kth(int k) {
    int sum = 0, x = 0;
    for (int i = 17; i >= 0; --i) { // 需满足 sum < k
        x += 1 << i; // 尝试扩展
        if (x >= n || sum + C[x] >= k)  x -= 1 << i; // x 不在树状数组范围内，或扩展失败
        else sum += C[x];
    }
    return x + 1;
}

[省选联考 2020 A/B 卷] 冰火战士。将温度离散化，那么求的就是冰人前缀和（$I_p$）和火人后缀和（前缀和记为 $F_p$）的最小值最大为多少。由于能力值不为负，因此只需要求出 $I_p\le F_{sum}-F_{p-1}$ 的最大 $p$ 和 $I_p\ge F_{sum}-F_{p-1}$ 的最大 $p$（但是 $F_{p-1}$ 最小）。

前者好搞，但是后者怎么求？考虑将 $F$ 平移一位，条件一变成 $I_p\le F_{sum}-F_{p}$，条件二变成 $I_p\ge F_{sum}-F_{p}$。当求出前面的 $p$ 后，取 $p\leftarrow p+1$，那么此时 $p$ 就是满足条件二的最小 $p$，然后再次倍增出最大的 $p$ 即可。代码。

例题

更多注重于分析。

[Ptz 2022 Summer Day 2] Ternary Search

Portal.

我们只需要考虑单谷。

谷的值是可以确定的。如果我们将谷左边的数全部取相反数，那么答案就是全局的逆序对数。

也就是说，我们通过是否取相反数来确定其应该是在谷值的左边还是右边。如果取相反数，那么它在左边，它对答案的贡献是在它左边比其小的个数 $L_i$；如果不取相反数，那么其对答案的贡献就是正常计入逆序对统计了。

也就是说，我们可以正常求逆序对的个数，当其走到左边的时候，我们就在树状数组上撤销它的贡献。何时它会跑到左边？当在它左边有 $x$ 个比它小的数，右边有 $x$ 个比它小的数的时候，就会切换，此时直接继承原来的贡献即可。树状数组上倍增即可。代码。

线段树

线段树是一种功能强大的二叉数据结构，可以维护半群上的信息（满足结合律）。

对于一般情况，我们使用堆式线段树来存储线段树；对于空间开不下的情况，我们使用动态开点来存储线段树。

线段树基本结构

这里不再赘述线段树的基本结构，但是它是一个很有用的东西。

首先无脑考虑逆时旅人，将删点改成加点。这样一定是更好做的。

最主要的问题是，如何用一种方式来压缩图？对于一个没有被删点的连续 $2^i$ 段，一定是连通的。这是什么？

线段树。

注意一个位置只会被删除一次，这很好，我们可以在线段树上区间染色，代表这些点存活到了 $i$ 时刻。

这样对于动态开点线段树上的存在的点，才是有意义的点，其余所有点都可以被映射到它们身上。对于每个节点将在 $\min\{ls_i,rs_i\}$ 时刻将它的左右儿子分裂开（不再连通），并查集维护即可。代码。

延迟标记

这个东西不只被用在线段树上，但从线段树结构基本可以介绍出它的大部分应用。以下问题都可以直接使用多元标记来处理：

• 区间最大子段和：维护前缀后缀最大子段和、区间和和答案即可；
• 区间平方和：不难根据区间和计算出新的区间平方和；
• 区间加等差数列单点求和：每个点维护一个 $d$，代表其加上的是 $d\times i$，其中 $i$ 是下标，然后再维护一个区间加标记即可。

将广义斐波那契数列的前两项作为标记打在线段树中，合并时直接加起来就可以。再加上斐波那契数列的求和公式：$\sum_{i=1}^{n}f_i=f_{n+2}-f_{2}$，和便可以直接计算。代码。

矩阵乘法维护标记

当标记大于一个的时候，我们就需要思考不同标记在下传过程中的相互影响，然而这很麻烦。因此，通过构造向量和矩阵乘法，可以很好地简化这类问题。

区间加区间乘是一个经典问题，我们在统计信息时需要直到当前点的和和区间长度，因此维护：

$$\begin{bmatrix} sum\\ len \end{bmatrix}$$

加法操作的矩阵是 $\begin{bmatrix}1 & c\\0 & 1\end{bmatrix}$，乘法操作的矩阵是 $\begin{bmatrix}k & 0\\ 0 & 1 \end{bmatrix}$，这样就转化成了一种操作。

[ICPC2021 Nanjing R] Paimon Segment Tree，因为这道题的存在，我想称这种技巧为“派蒙标记”。

线段树上一个结点维护 $\begin{bmatrix}s & a^2 & a & len\end{bmatrix}$ 代表累加和、区间平方和，区间和和区间长度，扫描线维护版本维，所有的信息都可以直接维护。代码。

派蒙线段树的经典应用是维护历史版本和，很容易使用矩阵描述这个东西。

对于这种子区间求和的问题，其本质就是历史版本和。扫描线扫一端，然后维护历史版本和。

常数过大，需要将矩阵拆除，具体地，由于矩阵上不是 $0/1$ 的位置只有 $9$ 个，因此维护这些位置的值即可。代码。

李超线段树

考虑这样一个问题：加入给定定义域的一次函数，查询 $x=k$ 时的最小值。

怎么做？考虑一种线段树，维护 $[l,r]$ 的节点只存储一个 $mid$ 处值最小的线段。修改操作如何实现呢？如果修改的线段不比当前线段优，那么下传修改线段；如果修改线段比当前线段优，那么下传当前线段。也就是说，要下传的一定是那个更劣的线段。如何下传？只有当在某一部分的线段有交点时才需要下传。

单次修改时间复杂度为 $O(\log^2 n)$，查询时直接记录路过的所有线段的答案即可，时间复杂度依然为 $O(\log n)$。

inline void pushup(int o, int l, int r) {
    T[o].v = min({T[o].v, T[o << 1].v, T[o << 1 | 1].v}); 
    T[o].v = min({T[o].v, calc(T[o].s, dis[idx[l]]), calc(T[o].s, dis[idx[r]])}); 
}
void update(int o, int l, int r, int x, int y, Seg k) {
    int mid = l + r >> 1; 
    if (x <= l && r <= y) {
        if (calc(k, dis[mid]) < calc(T[o].s, dis[idx[mid]])) swap(k, T[o].s); // 中点处 x 当前线段比 k 劣
        if (calc(k, dis[idx[l]]) < calc(T[o].s, dis[idx[l]])) update(o << 1, l, mid, x, y, k); 
        if (calc(k, dis[idx[r]]) < calc(T[o].s, dis[idx[r]])) update(o << 1 | 1, mid + 1, r, x, y, k); 
        return pushup(o, l, r); 
    }
    if (x <= mid) update(o << 1, l, mid, x, y, k); 
    if (mid < y) update(o << 1 | 1, mid + 1, r, x, y, k); 
    pushup(o, l, r); 
}

吉司机线段树

指的是一类维护区间最值操作与历史最值的线段树（Segment Tree Beats）。

区间最值操作

每个节点维护最大值，严格次大值和最大值的数量。这样遍历节点时有三种情况：

• $ma\le x$，那么无影响。
• $se<x<ma$，可以直接打上延迟标记计算。
• $x\le se$，暴力递归。

大概势能分析一下加上实际表现证明，其时间复杂度为线性对数。

区间历史最值

每个节点维护一个二元标记 $(p,q)$，代表先加 $p$ 再对 $q$ 取 $\max$。那么标记的合并就是 $(p_1+p_2,\max\{q_1+p_2,q_2\})$。这个东西存在颜色段均摊，因此时间复杂度为 $O((n+q)\log n)$。使用这种多元标记思想可以处理绝大部分的历史最值问题。

CPU 监控。考虑没有染色操作怎么做。简单，维护最大的历史加标记。

发现一次染色后所有的加都可以转化为染色，因此染色后直接开始维护标记即可避开讨论。

int n, m, a[100005];
struct Node {
    int mx, hmx, setv, addv, hset, hadd, tag; 
    void cover(int v, int hv) {
        setv = mx = v; addv =-0; 
        if (tag) hset = max(hset, hv);
        else hset = hv, tag = 1;
        hmx = max(hmx, hv); 
    }
    void add(int v, int hv) {
        hadd = max(hadd, addv + hv);
        hmx = max(hmx, mx + hv);
        addv += v; mx += v;
    }
    void change(int v, int hv) {
        if (tag) cover(setv + v, setv + hv);
        else add(v, hv);
    }
} T[400005];
inline void pushup(int o) {
    T[o].mx = max(T[o << 1].mx, T[o << 1 | 1].mx); 
    T[o].hmx = max(T[o << 1].hmx, T[o << 1 | 1].hmx); 
}
inline void pushdown(int o) {
    T[o << 1].change(T[o].addv, T[o].hadd);
    T[o << 1 | 1].change(T[o].addv, T[o].hadd);
    T[o].addv = T[o].hadd = 0;
    if (T[o].tag) {
        T[o << 1].cover(T[o].setv, T[o].hset);
        T[o << 1 | 1].cover(T[o].setv, T[o].hset);
        T[o].tag = 0;
    }
}
void update(int o, int l, int r, int x, int y, int k, bool type) {
    if (x <= l && r <= y) return type ? T[o].cover(k, k) : T[o].change(k, k), void(); 
    int mid = l + r >> 1; pushdown(o); 
    if (x <= mid) update(o << 1, l, mid, x, y, k, type); 
    if (mid < y) update(o << 1 | 1, mid + 1, r, x, y, k, type); 
    pushup(o); 
}

扫描线

对于一个高维空间的坐标限制，我们称之为 $B$ 维正交范围问题，我们可以利用扫描线将其降维。也就是说，扫描线维护一维，数据结构维护另一维。

差分处理

如果维护的信息可以差分，那么直接差分掉。比如矩形面积并问题，静态区间内不同数个数问题。将问题转化为矩形操作，然后扫描线维护。

此问题的基础形态是二维数点：平面上有 $n$ 个点 $(i,a_i)$，每次查询一个矩形内的点的个数。此矩形是一个 4-side 的矩形，可以通过差分的方式将其转化为 3-side，然后再扫描线维护一下变成 2-side，这样就成了一个平凡的单点修改区间查询的问题。

二维数点模型非常的有用，类似于以下问题都可以处理：

• 矩形面积并。4-side 差分成 3-side 的修改，然后扫描线扫描，线段树维护时看是否被覆盖来进行 pushup，最后查询全局被覆盖的数量。
• 将 $x$ 转化为 $l$ 的限制，$y$ 转化为 $r$ 的限制，然后看 $i$ 会对哪些 $[l,r]$ 产生贡献，最后是矩形面积加和。

也就是说，差分和扫描线是我们的降维手段，最后一个 2-side 的问题就是平凡的，使用合适的数据结构（区间修改单点查询，单点修改区间查询，区间修改区间查询）维护即可。

类似的还有其它的数点问题，比如三维偏序（CDQ + 扫描线 + 数据结构），强制在线的二维数点（可以使用主席树），强制在线动态二维数点（必须树套树），使用合理的手段进行降维即可。

注意，扫描线不一定要扫时间维，可以扫序列维，也就是说，如果单点修改可以轻松撤销，那么区间修改就退化成了单点修改，然后数据结构维护操作序列操作的过程。

哎我会维护奇数！所以这道题就是直接区间所有出现数的异或和异或掉奇数异或和。前者可以采用扫描线，只维护这个数最后一次出现的位置的贡献。

先假定 $n+1$ 个数全部出现，然后考虑数 $i$ 不出现的条件：

1. 所有的 $i$ 都出现在 $[l,r]$ 内；
2. 所有的 $i-1$ 都不出现在 $[l,r]$ 内。

然后就是扫描线限制矩形即可。代码。

扫描线维护右端点 $r$，维护 $s_i$ 代表 $\sum_{p\le i} \sum_{p\le q\le r}f(p,q)$，那么答案为 $s_r-s_{l-1}$。

记扫描到当前状态时，$A,B,C$ 分别代表运算之后的后缀结果。

当 $r\rightarrow r+1$ 时，考虑 $s_i$ 如何改变。如果 $A_i,B_i,C_i$ 均没有发生变化，那么 $s_i$ 的变化量和上次一样，将它们的“更新标记”的时间戳增大 $1$ 即可（实际上只需要记录更新时间，然后维护每个节点的最后更新时间）。

只有后面一段 $O(\log V)$ 的区间的 $f$ 值不同于 $r$ 变化之前的（设为 $p$）。对于 $[p,r]$ 直接暴力计算它们在当前 $r$ 下的贡献的增量。具体来说，维护一个 $v_i$ 代表 $\sum_{l=1}^{i}f(l,r)$ 就可以直接计算。

时间复杂度 $O(n\log V+m)$，离线后手写内存池卡常即可。代码。

分治处理

线段树合并

可以以 $O(n\log n)$ 的时间合并两棵满线段树的信息。但对于常用的在树上进行线段树合并，由于每棵线段树初始只用一个信息，因此总时间复杂度是 $O(n\log n)$ 的。

int merge(int p, int q, int l, int r) {
    if (!p || !q) return p + q; 
    if (l == r) return T[p].cnt += T[q].cnt, p; 
    int mid = l + r >> 1; 
    T[p].ls = merge(T[p].ls, T[q].ls, l, mid); 
    T[p].rs = merge(T[p].rs, T[q].rs, mid + 1, r);
    pushup(p); return p; 
}

颜色段均摊

对于区间染色操作，每次只会增加 $O(1)$ 个连续颜色段，均摊的颜色段插入删除次数为 $O(n+m)$。

对于区间染色类问题（区间染色、排序等操作），用珂朵莉树维护类的问题，都存在颜色段均摊。存在 $2\sim 3$ 倍的常数。

struct Node {
    int l, r; mutable int v; // 这个 v 接下来需要修改
    Node(int l = 0, int r = 0, int v = 0) : l(l), r(r), v(v) {}
    bool operator< (const Node &a) const { return l < a.l; }
};
set<Node> T;

inline auto split(int p) {
    if (p > n) return T.end(); 
    auto it = T.lower_bound(Node(p));
    if (it != T.end() && it->l == p) return it;
    --it; int l = it->l, r = it->r; i64 v = it->v;
    T.erase(it); T.insert(Node(l, p - 1, v));
    return T.insert(Node(p, r, v)).first;
}

我们记一个 $c$ 代表区间颜色，不一样时记为 $-1$。如果一样则打标记修改，不一样则暴力递归修改。一次区间染色只会产生两个新的端点，暴力查询的次数为 $O(n+m)$ 级别。因此时间复杂度为 $O((n+m)\log n)$。代码。

单侧递归结构

使用线段树维护。一个节点记录两个数：区间所对应的答案，当前区间的最大斜率。修改时很容易实现，关键是，pushup？问题在于如何统计当前节点的答案，也就是说，如何统计右半段在被左半段影响之后应该如何计算答案。怎么办？不会！俗话说的好，那么直接递归下去！

如果右区间的最大值小于等于左区间，那么就被全部挡住了。否则递归考虑右半段，这样所有的贡献都可以计算。

#include <bits/stdc++.h>
using namespace std;

int n, m;

struct Node {
    int v; double k;
} T[400005];
double a[100005];

int pushup(int o, int l, int r, double k) {
    if (T[o].k <= k) return 0; if (a[l] > k) return T[o].v; 
    if (l == r) return 0; 
    int mid = l + r >> 1; 
    if (T[o << 1].k <= k) return pushup(o << 1 | 1, mid + 1, r, k); 
    return pushup(o << 1, l, mid, k) + T[o].v - T[o << 1].v; 
}

void update(int o, int l, int r, int x, int k) {
    if (l == r) return T[o] = {1, a[x]}, void();
    int mid = l + r >> 1;
    if (x <= mid) update(o << 1, l, mid, x, k);
    else update(o << 1 | 1, mid + 1, r, x, k);
    T[o].k = max(T[o << 1].k, T[o << 1 | 1].k);
    T[o].v = T[o << 1].v + pushup(o << 1 | 1, mid + 1, r, T[o << 1].k);
}

int main(void) {
    ios::sync_with_stdio(0); 
    cin >> n >> m; 
    while (m--) {
        int x, y; cin >> x >> y; a[x] = 1.0 * y / x;
        update(1, 1, n, x, y); cout << T[1].v << "\n"; 
    }
    return 0;
}

快速求解括号匹配可以使用哈希，由此不难得出一个序列分块的做法。这里我们考虑 $\log$ 做法。

我们考虑将整个结构放到线段树上，当匹配完之后，还剩下 $\log$ 个哈希值，这样直接合并即可。

如何合并两段的哈希值？对于每个节点，其匹配后必定剩余一堆左括号或者一堆右括号。用 $vr$ 代表右括号的匹配情况，$vl$ 代表左括号的匹配情况。在合并时，我们需要求解一定长度的括号的哈希值，这在线段树上单侧递归下去就可以实现。

对于求解一段的一定长度的哈希值，我们也可以在线段树上单侧递归下去来求解。代码。

函数最值的动态维护

时间复杂度分析可以参考 EI 的博客 或者集训队论文。KTT 用于维护增量函数的最值。我们维护 $x$ 变大后子树里使得某个 $\max$ 所取函数第一次发生改变的 $x$ 的值，当下一次询问超过这一 $x$ 时，我们递归下去将发生替换的部分重置。

模板。求最大子段和需要维护 $sum,lmax,rmax$ 和 $ans$。我们考虑区间加操作对它们的改变。

区间加 $k$，如果答案选择的区间没有改变，那么该值会增加 $lk$，$l$ 为选择的区间长度。四个信息改用一次函数来维护，使其表示 $ls+b$。这样就可以直接计算影响。

线段树每个节点维护一个 $x$，表示区间加超过 $x$ 时，答案选择区间会发生改变。pushup 时，$x$ 要对三个变量的不同方案的交点取 $\min$。

修改时间复杂度为 $O(\log^3 n)$。代码。

例题

线段树的更多技巧可以在这里找到！

[Luogu P5278] 算术天才⑨与等差数列

Portal.

发现条件非常严苛，因此可以考虑哈希之类的方法，这里不做赘述。

一段区间可以重排为等差数列，当且仅当满足（$d=0$ 先特判掉）：

• $\max -\min =d\times (len-1)$；
• $\gcd_{i=l}^{r-1}(a_{i+1}-a_i)=d$；
• 序列中没有重复的元素。

用线段树维护即可。第三条可以使用 set、map 维护一个数最左边的出现位置，然后用线段树维护这个值的最小值，如果这个数小于 $l$，那么一定没有重复元素。代码。

* [Ynoi2015] 纵使日薄西山

考虑哪些数可以被减。如果我们开始减 $a_i$，那么它一定会一直减下去（因为左右两个永远都比它小）。

将原序列进行单调极长划分，发现对于每个极长单调区间，答案一定是所有奇数位置或者所有偶数位置的和。使用一个 set 存储所有的极长单调区间分割点（称为极值点，令一个极值点代表极长单调区间的结束），修改一个数时最多只会影响到五个极值点（修改一个极值点可能使它右边的极值点不存在，进而影响右边第二个极值点，左边同理），复杂度可以接受。

根据此维护即可，细节很多。代码。

[NOI2022] 众数

Portal.

区间绝对众数也必定是中位数，这样建立权值线段树，然后就可以直接线段树二分，然后检查出现次数是否合法即可。再用一个链表辅助合并序列就完成了，代码。

* [NOI2020] 命运

Portal.

考虑设 $f_{x,y}$ 代表以 $x$ 为根的子树中已经全部满足，不满足的距离最多为 $y$（从根节点向下开始）的方案数，答案为 $f_{1,0}$。

考虑每次将 $(x,y)$ 合并进当前答案，分别考虑这条边填 $1/0$ 的贡献：

$$f'_{x,i} \leftarrow \sum_{j=0}^{dep_x} f_{x,i}f_{y,j}+\sum_{j=0}^{i} f_{x,i}f_{y,j}+\sum_{j=0}^{i-1} f_{x,j}f_{y,i}$$

设 $g_{x,y}=\sum_{i=0}^y f_{x,i}$，则：

$$f'_{x,i}=f_{x,i}(g_{y,dep_x}+g_{y,i})+f_{y,i}g_{x,i-1}$$

所有的转移位置都只与深度有关，因此直接线段树合并，维护区间乘法的修改。代码。

[CF793F] Julia and snail

Portal.

扫描线扫一遍序列，遇到一条绳子 $(l,r)$ 相当于 $\forall i\le l\wedge a_i\ge l,a_i\leftarrow \max\{a_i,r\}$，实际上是 $a_i\leftarrow r$，SGT Beats 维护即可。

具体地，每个节点维护最大值和次大值，修改使用二元组 $(p,q)$ 来表示，代表 $\forall a_i\ge p,a_i\leftarrow q$。

如果 $ma<p$，那么这个区间不会动；如果 $se<p\le ma$，那么只有最大值会动；如果 $p\le se$，那么递归处理。代码。

* [Ynoi2013] 对数据结构的爱

Portal.

考虑模拟这个过程。我们需要知道对于一段区间，到底会减去多少个 $p$。

搞一个数组 $c_i$ 代表这段区间要减去 $i$ 个 $p$ 的最小初始值，那么查询的时候直接二分就行。现在考虑如何计算 $c$ 数组。

尝试枚举左儿子的 $c_x$ 和右儿子的 $c_y$ 来计算 $c_{x+y}$，什么时候不能更新？$c_x$ 的上界经过操作后依然小于 $c_y$。

用 $\max\{c_x,c_y+x\times p-sum_{ls}\}$ 更新 $c_{x+y}$。由于 $c_{x+1}-c_{x}\ge p$，因此直接双指针扫就行。

单次询问会拆成 $\log$ 个区间，每个区间用 $\log$ 时间二分，时间复杂度为 $O(n\log n+m\log^2 n)$。代码。

平衡树

其同样为二叉数据结构，满足所谓的“BST 性质”。

笔者通常使用 FHQ 来实现平衡树。

FHQ-Treap

FHQ 利用分离与合并来进行维护，然后通过随机权值来保证平衡。

值得注意的是，如果采用指针实现，那么 FHQ 会很快，而且非常好写。大概像这样：

struct Node {
    int rnd; 
    Node *ls, *rs; 
} T[5000005];   
Node* root; int tot; 
inline Node* newNode(int col, int l, int r) { return &(T[++tot] = Node(/*...*/)); }

替罪羊树

替罪羊树是一种依靠重构操作维持平衡的重量平衡树。替罪羊树会在插入、删除操作时，检测途经的节点，若发现失衡，则将以该节点为根的子树重构。

首先，如前所述，我们需要判定一个节点是否应重构。为此我们引入一个比例常数 $\alpha$（一般采用 $0.7$），若某节点的子节点大小占它本身大小的比例超过 $\alpha$，则重构。

例题

相比于线段树，平衡树的题不是很多。

[HNOI2011] 括号修复

Portal.

修复一个括号序列的代价这样计算：设 ( = -1, ) = 1，前缀最大值为 $a$，后缀最小值为 $b$，代价是 $\lceil a\div 2\rceil+\lceil -b\div 2\rceil$。然后直接使用平衡树维护即可。代码。

[NOIP2017] 列队

Portal.

使用平衡树维护每一行和最后一列，每个点存储一段区间即可。代码。

[ZJOI2006] 书架

Portal.

问题在于如何高效找到一个节点在平衡树上的位置（中序遍历的编号）。维护每一个节点的父亲，然后直接从这个节点的位置跳到根，维护中序遍历的位置。这之后直接乱做即可。代码。

* [POI2015] LOG

Portal.

使用一棵维护权值的平衡树。在减 $1$ 的过程中，大于等于 $s$ 的是随便用，剩下的只需要考虑它们的和是否够用即可（可以将后面的向前移来叠到 $s$，这样保证一层中不会有来自同一个位置的数）。代码。

* [Luogu P3987] 我永远喜欢珂朵莉~

Portal.

一个数最多被除 $\log$ 次，那么可以暴力修改并使用 Fenwick 树查询，使用平衡树维护有因数 $x$ 的数，每次修改时直接 DFS 分裂出的子树。时间复杂度 $O(nd(V)+n\log n\log v+m\log n)$。代码。

对于数据加强版 [Ynoi2013] 大学，平衡树常数过大，不能通过。对于每一个约数采用一个并查集，开始时每个数都指向自己，删除时将当前数的父亲设置为下一个数。另外 STL vector 的常数过大，需要手写内存池。代码。

[CF702F] T-shirts

Portal.

由于每个人的处理方式都是一样的，因此不如考虑每个物品对于人的贡献。那么不难对于人直接维护，然后打上个减标记。对于位置会改变的东西，直接暴力插入，这样只会发生 $\log c$ 次，因此复杂度是对的。代码。

[Ynoi2011] 遥远的过去

Portal.

平衡树求出 $a$ 的所有子串的哈希值，只需要支持删除一个元素，加入新元素前给以前的东西打一个标记即可。代码。

** [Ynoi2015] 人人本着正义之名

Portal.

首先看一看操作 $3\sim 6$ 是个什么东西。

将 $[l,r-1]$ 中的数 $a_i$ 同时变为 $a_i$ 与 $a_{i+1}$ 按位或的值？简单，就是所有极长 $0$ 段最右边一个 $0$ 变成 $1$。

搞一个平衡树，打一个标记表示左右端点的移动量。只有两个问题：

• 如何保证区间极长？区间染色时向左右拓展一下即可。
• 如何保证没有空区间？区间数量是 $O(n+m)$ 的，维护最短 01 区间长度，暴力找，然后将其左右区间合并即可。

本质上不难，但代码比较壮观，需要使用指针实现平衡树进行卡常，代码。

* [NOI2021] 密码箱

Portal.

我们需要用数据结构描述这些操作，考虑使用连分数表示 $f$ 的值：

$$a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\cdots}}$$

为了接下来方便操作，我们取其倒数进行计算。考虑其在合并时发生了什么，不难发现：

$$\frac{a'}{b'}=\cfrac{1}{a_i+\cfrac{a}{b}}=\cfrac{b}{a_i\times b + a}$$

那么这个操作就可以用矩阵来描述了：

$$\begin{bmatrix} a' & b' \end{bmatrix} = \begin{bmatrix} a & b \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 1 & a_i \end{bmatrix}$$

接下来要描述 W 和 E 操作。首先考虑 W 操作，可以构出 W 为 $\begin{bmatrix}1 & 1 \\ 0 & 1\end{bmatrix}$。

然后是 E 操作。当 $a_k>1$ 时，不难发现其为 $\begin{bmatrix} 0 & -1 \\ 1 & 2 \end{bmatrix}$，实际上对 $a_k=1$ 也满足。

然后直接上平衡树维护即可。注意你的常数，代码。

* [湖北省队互测 2014] 没有人的算术

Portal.

为什么不好做？我们无法轻易比较这个东西。

只有 $O(m)$ 个不同的数，考虑给每个数都赋一个实数权。维护一棵平衡树，每次插入一个 pair<double, double>，代表新的数的权值，和平衡树上的每个节点比较（节点存储它的 double 和它是由哪两个 double 组成的），节点的权值由动态标号而来，实际上是 $(l+r)/2$，代表着 dfn 序，而平衡树上的 dfn 序就代表着大小。这个 trick 也称为动态标号。

由于我们不知道插入的东西的大小无法分裂，而旋转的复杂度又无法保证（是子树大小的）。因此只能使用替罪羊树。代码。

持久化数据结构

我们对于一个数据结构，想维护其所有的历史版本。这样的数据结构称为持久化数据结构。

• 部分持久化：版本序列是链式结构；
• 完全持久化：版本序列是树状结构；
• 可合并持久化：支持合并，也就是说版本是 DAG 结构。

但是在算法竞赛中，持久化最常见的作用是降维。

算法竞赛通常采用 Path Copy，也就是修改时新建节点的方式来实现持久化数据结构，要求数据结构是一棵有根树形态。

持久化线段树

采用动态开点线段树，修改时新建节点即可。

对于持久化线段树的区间修改操作，如果标记可以永久化，那么最好这样做，因为这样可以节省很多空间。否则需要下传标记，所有的下传的点都必须复制后再下传。

我们可以很方便地在多棵持久化线段树上同时进行二分，直接都加起来就行。

其它持久化数据结构

仿照持久化线段树的思路，其它非均摊复杂度数据结构也是可以持久化的。

• 持久化数组：通常利用持久化线段树来实现持久化数组，进而实现不能路径压缩的持久化并查集。
• 持久化 Trie：与持久化线段树原理大致相同，在新建节点的时候复制一下就行。同时应注意，我们可以简单地在多棵 Trie 上二分，直接都加起来就行。
• 持久化平衡树：通常情况下持久化 FHQ 足够应付大部分的问题，其余的也不太能见到。如果见到了区间平移之类的操作，那么大概率就是持久化平衡树，在分裂和合并的时候新建一下节点即可。直接复制随机权值是错的，应该按照树的大小作为依据按照概率进行合并。

例题

有些东西比较麻烦。

[THUSC2015] 异或运算

Portal.

将求第 $k$ 大转化为 $k$ 小，看一下 $n=1$ 怎么做？对 $Y$ 建立持久化 01 Trie，然后拿着 $X[1]$ 开始从高到低位开始贪心。答案的这一二进制位能取到 $0$ 的个数如果小于 $k$，那么这一位就需要取 $1$，然后令 $k$ 减去这个个数；否则这一位取 $0$。

发现 $n,q$ 都不是很大，因此对于 $n>1$ 直接暴力扫一遍，把总和加起来跟 $k$ 比即可。代码。

[CF1665E] MinimizOR

Portal.

如何处理或的最小值呢？如果出现了两个以上的 $0$，那么这一位显然填 $0$；如果没有 $0$ 出现，则填 $1$；有一个 $0$ 呢？找到这个 $0$ 的位置，让它自己往 $0$ 走，同时搞两个儿子就好了。只会增加 $\log$ 次节点，时间复杂度为 $O(n\log^2 V)$。代码。

*【UNR #1】火车管理

Portal.

操作一和操作三可以简单地使用线段树维护。对于操作二，将线段树持久化，在染色时记录每个节点染的是哪一个版本的颜色，这样在回退时就可以查询染色的版本号，然后将其染成它上一个版本的颜色。

依然注意，持久化线段树的带标记下传区间修改空间常数很大，需至少开到平时的两倍。代码。

[CF1422F] Boring Queries

Portal.

对序列建立一棵持久化线段树，将数质因数分解掉，然后在左端点乘上相应的逆元即可。代码。

嵌套数据结构

K-D Tree 可以解决高维空间上的矩形修改矩形查询问题，而树套树和 CDQ 分治的功能是等价的，通常只能解决单点修改矩形查询类问题。

树套树

正常的树状数组每个点维护的是一个数，如果改成维护一棵平衡树，那么就成了“树状数组套平衡树”。

不一定是手写数据结构的嵌套，有些时候存在一些类似于嵌套结构的题目。

这里通过几道简单的题来简单介绍一下树套树。

【模板】二逼平衡树（树套树）

Portal.

如果使用线段树套平衡树，那么再查询排名为 $k$ 的数的时候就需要在外层二分（平衡树上多树二分非常复杂），时间复杂度为 $O(n\log^3 n)$。代码。

*「C.E.L.U-02」苦涩

Portal.

建立一棵线段树，每个节点保存一个优先队列作为区间加的标记，并永久化（即当前节点的优先队列中的内容对它的儿子都有效）。删除时可以暴力遍历线段树，因为每一次添加只会添加一个拥有最大数值最大的颜色段，这样删除它的时间就会在 $O(\log n)$ 级别。若 $n,m$ 同阶，那么总时间复杂度为 $O(n\log^2 n)$。代码。

[ZJOI2017] 树状数组

Portal.

方向反了是什么？变成了求后缀和！也就是说，但是整个东西求的是 $S_{r-1}-S_{l-2}$。也就是说，要求 $v_r=v_{l-1}$ 的概率。那么可以视作区间修改，单点查询。

使用二维线段树，外层维护 $l$，内层维护 $r$，新的概率是很好求的，注意 $l=1$ 时只需要注意 $r$ 的变化情况，直接维护即可。代码。

* [THUSC2021] 搬东西

Portal.

先求解一轮可以放置多少个物品，贪心完成。然后二分出第一个最大选择的下标，使用树状数组套权值线段树完成。代码。

K-D Tree

K-D Tree 具有二叉搜索树的结构，每个节点都对应了 $k$ 维空间上的一个点。

为了保证 K-D Tree 的树高，

简单树形问题

对于树上问题有基本的处理方法，比如 LCA、树形 DP、树上差分等，在此不做赘述。

常见树形问题处理手段：

• 树形 DP；
• 直径重心及其性质；
• 树上链信息维护，差分、重链剖分、树上倍增；
• 树上路径信息统计：树分治；
• 线段树合并、两种树上启发式合并；
• 离线，挂信息到节点上；
• DFS 序、括号序、欧拉序。

树的重心的性质：以任意节点为根，树的重心的子树大小 $\ge \frac n 2$。

DFS 搜索树的性质：只存在返祖边，不存在横叉边。

[Ynoi2008] stcm。直接对于 DFS 序进行分治，因为都包含一个 $mid$ 的子树区间一定是相互包含的，因此直接增量添加信息即可。代码。

求树上两条链的交，设要求两条链 $(a,b),(c,d)$，求出 $(a,c),(a,d),(b,c),(b,d)$ 的 LCA，取深度最深的两个，如果不相等则就是相交的链，如果相等，要看这个位置的深度是否比两条链本深的 LCA 都深，如果满足则它自己是唯一的交点，否则不相交。代码。

笛卡尔树

笛卡尔树是一种特殊的 Treap，其节点权值不再是随机的，而是给定的。每个节点的权值用 $(x_i,y_i)$ 表示，只考虑 $x$ 时它是 BST，只考虑 $y$ 时它是堆（此处以小根堆为例）。

在 $x$ 递增时，我们可以以线性复杂度建出笛卡尔树。插入新节点时，为了保证 $x$ 的性质满足，要将 $x$ 插入到尽量右的地方。

具体来讲，维护一个从根节点一直走到右儿子的链。设当前需要插入 $u$，则需要找到第一个 $y_v>y_u$，将 $v$ 的右儿子设为 $u$（不存在则将 $u$ 设为根），如果 $v$ 原本有右子树，则将 $v$ 的右子树改连在 $u$ 的左子树下面来满足 BST 性质。使用单调栈维护此链，时间复杂度为 $O(n)$。

模板题核心代码如下：

for (int i = 1, tot = 0, cur = 0; i <= n; ++i) {
    scanf("%d", p + i); cur = tot; 
    while (cur && p[st[cur]] > p[i]) --cur;  
    if (cur) rs[st[cur]] = i; 
    if (cur < tot) ls[i] = st[cur + 1]; // 放到左节点以满足 BST 性质
    st[++cur] = i; tot = cur; 
}

性质：如果节点编号 $1\sim n$ 为 BST 权值，然后点权满足小根堆性质，那么 $\min\{a_x,\cdots,a_y\}=a_{\operatorname{LCA}(x,y)}$。

树链剖分

我们对于链上的问题更为熟悉，因此在遇到树上问题时，可以考虑使用树链剖分将其转为链上问题再进行求解。常见类型有两种：

重链剖分。最为传统的形式，最常用于将树剖成 $O(\log n)$ 条链。一个比较好的性质是，每次选择重儿子跳，那么树的规模都会减小一半。

我们在处理某些问题时，可以选择只考虑当前节点轻儿子的答案，这样在重链上修改 $O(\log n)$，只有 $O(\log n)$ 个节点的答案会重新计算。

长链剖分。在处理与深度相关的问题时可能有奇效（实现启发式合并），但是基于长链剖分实现的 $O(1)$ K 级祖先甚至打不过暴力跳的重链剖分！

例题

比较杂。

* [CF1580D] Subsequence

Portal.

先来看一下要求的这个东西：

$$\begin{aligned} \text{原式}&=\sum_{i = 1}^m (m \cdot a_{b_i}) - \sum_{i = 1}^m \sum_{j = 1}^m f(\min(b_i, b_j), \max(b_i, b_j))\\ &=(m-1)\sum_{i = 1}^m a_{b_i}-2\sum_{i=1}^m\sum_{j=i+1}^m \min\{a_{b_i},a_{b_i+1}\cdots,a_{b_j-1},a_{b_j}\} \end{aligned}$$

要求这个东西的最大值，后面这个区间最小值可以考虑放到笛卡尔树上，然后用树形 DP 求解这个问题。

设 $f_{x,k}$ 代表 $x$ 中选择 $k$ 个节点的最大价值，初始 $f_{i,1}=(m-1)a_i$，然后转移是一个类似树形背包的过程：

$$f_{x,i+j}=\max\{f_{x,i}+f_{y,j}-2\times a_x\times i\times j\}$$

代码。

* [APIO2021] 封闭道路

Portal.

直接暴力树形 DP。设 $f_{x,0/1}$ 代表 $x$ 与父亲连接的边是否删除时，$u$ 的子树中满足所有节点的度数 $\le \text{lim}$ 的最小代价。转移时，将边按照 $f_{y,1}+w-f_{y,0}$ 扔到堆里，然后选前 $deg_x -\text{lim}$ 小的。这样当 $deg_x\le \text{lim}$ 时，就可以直接扔掉这个点（直接把 $w$ 扔到 $v$ 的堆里），每个点维护一个堆即可。代码。

[Ynoi2011] ODT

Portal.

每个点维护一棵 Treap，然后只维护轻儿子的信息，修改 $O(\log^2 n)$，查询 $O(\log n)$，可以维护若干个重儿子来平衡，但没必要。代码。

[CF536E] Tavas on the Path

Portal.

考虑给定 01 边权怎么做，线段树上维护前后缀 $1$ 段长度和答案，怎么都能和并，有限制的话直接按照边权排序依次加入即可。时间复杂度 $O(q\log^2 n+n)$，代码。

* [CF526G] Spiders Evil Plan

Portal.

首先 $k$ 条路径可以覆盖 $2k$ 叶子的树。也就是说，选择 $y$ 个点就是能选择 $2y$ 个叶子，然后极小连通块的边权和尽量大。

以 $x$ 为根时如何选择叶子呢？考虑进行一次长链剖分，那么 $x$ 所在的长链的叶子也一定选择了，然后按照边权排序贪心即可。

多次询问怎么办？由于树上经过 $x$ 的最长链一定经过直径的某一端，那么以直径的两个端点分别做一次长链剖分，然后要想办法将 $x$ 加入连通块，如果一开始没有满足，那么只有两种方法：

• 将贡献最小的长链去掉，然后加入 $x$ 所在长链；
• 找到离 $x$ 最近长链的下半部分并替换。

倍增跳长链即可。代码。

树分治

树分治常用来被解决路径统计问题。一般情况下什么分治好写，就用什么就可以了。

静态点分治

树的点分治每次找一个重心，然后统计经过重心的路径，然后把这个点删去，树变成了很多连通子图，递归下去计算。

我们先任意选择一个节点作为根节点 $root$（显然重心比较好），所有完全位于其子树中的路径可以分为：

• 不经过当前根节点的路径；
• 经过当前根节点的路径，又可以分为两种：
  • 以根节点为一个端点的路径；
  • 跨越根节点的路径，实际上是有两条以一个根节点为端点的路径合并而成，分治的时候只需要合并这种信息。

找到重心 $r$ 作为分治中心，打上删除标记，并 dfs 它的每一棵子树。求出子树内每个节点到分治重心的距离和来源于哪个儿子的子树，统一存在一个 vector 里，使用双指针来合并答案（注意只能合并不同的子树）。

离线统一处理可以将时间复杂度降低为 $O(n\log n(m+\log n))$，正常单次点分治的时间复杂度为 $O(n\log n)$。代码。

静态边分治

每次找到一条边，然后统计经过这条边的路径。但是菊花图时的复杂度会直接爆炸，为此我们需要对树进行三度化。

对于度数比 $3$ 大的节点，可以通过加虚点（加上去不会改变信息的点）的方式来将树的节点度数改掉。类似于下图的方式：

静态链分治

使用树链剖分的结构，每次将一条链的信息进行合并。也就是所谓的“树上启发式合并”。根据情况使用重链剖分或长链剖分实现。

我们只关心每个节点内深度为 $j$ 的节点个数，那么深度相同的节点是等价的。设 $f_{i,j}$ 表示子树 $i$ 内深度为 $j$ 的节点个数，则 $f_{i,j}=\sum_{k\in son(i)}f_{k,j-1}$。

考虑长链剖分优化：对于重儿子，直接继承它的答案。然后合并轻儿子的答案，每个节点最多被合并一次。

因为所有点的深度之和加起来是 $O(n)$，因此时间复杂度线性。代码。

动态树分治

将点分治依次扫描的点拉下来即可建立点分树。对于不关心树的形态的问题，可以用这种方式处理。其关键性质是点分树上的 LCA 一定在原树的两点路径上；树高为 $O(\log n)$。

例题

本质还是分治，主要问题在于思考如何合并。

[JOISC2020] 首都

Portal.

要求的是一个含有颜色数最小的连通块，然后连通块内的颜色和块外两两不同，点分治暴力更新即可。代码。

* [Ynoi2013] 成都七中

Portal.

先转化要查询的信息：点 $p$ 到 $x$ 的路径上的点的编号在 $[l,r]$ 的点中，有多少种不同颜色的点。

直接点分治下去，一个询问第一次统计在合法路径能覆盖到它的时候，然后二维数点。时间复杂度 $O((n+m)\log^2 n)$。代码。

[PtzS 2019 Day2] Interactive Vertex

Portal.

直接点分治下去，每次需要二分，询问次数是 $O(\log^2 n)$ 的，每次需要排除至少一半的大小，因此二分时候带个权值即可。代码。

其它树上问题

树上问题还有一些其它结构，这里记录了几个常用的。

虚树

动态树

我们使用数据结构维护树上结构，但是对于动态树问题，我们不能简单地通过重链剖分来完成这个东西。

对于一个点连向它所有儿子的边，我们自己选择一条边进行剖分，我们称被选择的边为实边，其他边则为虚边。对于实边，我们称它所连接的儿子为实儿子。对于一条由实边组成的链，我们同样称之为实链，可以采用 Splay 来维护这些实链。

LCT 是用一些 Splay 来维护动态的树链剖分，我们将其成为“辅助树”。

例题

还有一些出现在树上的问题，但是说不太清它们到底是什么题。

[Ynoi ER2022] 虚空处刑

Portal.

首先，树上邻域信息一定只能维护子树的信息，否则单点修改会导致所有儿子都需要修改，复杂度直接爆炸。

令 $C_{i,j}$ 表示 $i$ 点所在子树范围内的连通块的 $j$ 色连通块序列，修改时直接启发式合并，只需要更新 $C_{fa_x,y}$ 即可。大概是双 $\log$ 的，代码。