基于线段树和树状数组的序列维护

线段树（Segment Tree）是一种二叉搜索树，1977 年由 Jon Louis Bentley 发明，可以较为灵活且效率较高地解决信息可合并的序列维护问题。而树状数组可以维护序列的前缀和。

更新日志

2023/7/14

开始大规模地更改代码，重构文章。

2023/6/30

补充没有理解透彻的内容，增加的部分内容和习题，删除了冗余的习题。

树状数组

又称 Fenwick 树、二叉索引树（BIT）。支持维护前缀后缀的信息。

概述

树状数组将序列拆分成了恰好 $n$ 个区间，对于每一个前缀求解都可以拆成 $\log p$ 个区间进行求解，而且自带一个卡不掉的 $1/2$ 的常数，随机数据下则为 $1/4$ 的常数！我们通过 $\operatorname{lowbit}$ 来支持树状数组的工作。

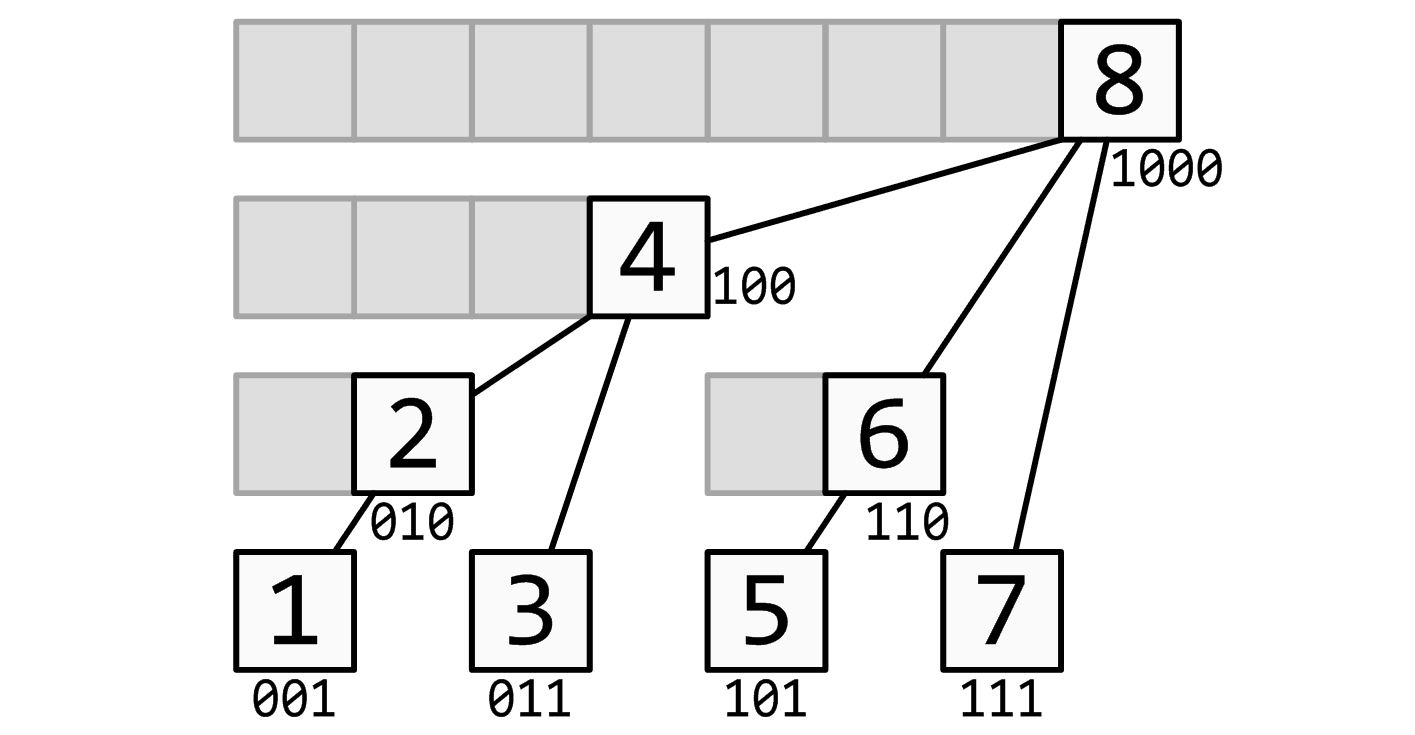
一个显式的树状数组

模板，区间和我们可以用前缀和相减来求解，代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 

int n, m; 
int a[500005]; i64 C[500005]; 

void add(int x, int k) { for (; x <= n; x += x & -x) C[x] += k; }
i64 sum(int x) { i64 r = 0; for (; x; x -= x & -x) r += C[x]; return r; }

int main(void) {
    scanf("%d%d", &n, &m); 
    for (int i = 1; i <= n; ++i) scanf("%d", a + i), add(i, a[i]); 
    while (m--) {
        int op, x, y; scanf("%d%d%d", &op, &x, &y); 
        if (op == 1) add(x, y); 
        else printf("%lld\n", sum(y) - sum(x - 1)); 
    }
    return 0;
}

树状数组自身也有许多漂亮的操作，虽然效率上略微胜于线段树和平衡树，但是可扩展性和直观程度上却不如它们。下面我们来看一些必须掌握的。

线性建树

对于树状数组上的每个节点都向上传递，具体过程如下：

for (int i = 1; i <= n; ++i) {
    int x; cin >> x; C[i] += x; 
    if (i + lowbit(i) <= n) C[i + lowbit(i)] += C[i]; 
}

差分与前缀和

树状数组可以轻松维护序列的高阶前缀和，首先将原序列差分可以直接解决区间加单点查询。

这里直接给出方法。对于 $k$ 阶前缀和，写出 $\dbinom{y-x+k-1}{k-1}$ 的多项式形式，然后 $y$ 表示的是下标， $x$ 表示的是当前位置的值。时间复杂度 $O(kq\log n)$ 。

权值树状数组

构建原序列的权值数列，然后利用树状数组统计。下面的代码可以快速解决逆序对问题：

查看代码

#include <bits/stdc++.h>
#define lowbit(x) (x & (-(x)))

using namespace std;
typedef long long i64;

inline int read(void) {
    int x = 0, c = getchar_unlocked(), f = 1;
    while (!isdigit(c)) {if (c == '-') f = -1; c = getchar_unlocked();}
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar_unlocked();
    return x * f;
}

int n, m, a[500005], b[500005];
int C[500005];

void update(int x, int k) {
    while (x <= n) {
        C[x] += k;
        x += lowbit(x);
    }
}

int query(int x) {
    i64 res = 0;
    while (x) {
        res += C[x];
        x -= lowbit(x);
    }
    return res;
}

int main(void) {
    n = read();
    for (int i = 1; i <= n; ++i)
        b[i] = a[i] = read();
    sort(b + 1, b + n + 1);
    m = unique(b + 1, b + n + 1) - (b + 1);
    for (int i = 1; i <= n; ++i)
        a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
    i64 ans = 0;
    for (int i = n; i >= 1; --i) {
        ans += query(a[i] - 1);
        update(a[i], 1);
    }
    printf("%lld\n", ans);
    return 0;
}

权值数组也可以实现名次树，但是当强制在线时就寄掉了。但是这引出了一个重要 trick：树状数组倍增。

树状数组二分与倍增

我们当然可以使用二分套树状数组达到 $O(n\log^2 n)$ 的复杂度，然而有没有更好的方式适配树状数组这种结构呢？有！倍增！

查询一个权值树状数组里的 $k$ 小值。

我们从二进制高位到低位枚举，时间复杂度为 $O(n\log n)$ 。

// 权值树状数组查询第 k 小
int kth(int k) {
    int sum = 0, x = 0;
    for (int i = 17; i >= 0; --i) { // 需满足 sum < k
        x += 1 << i; // 尝试扩展
        if (x >= n || sum + C[x] >= k)  x -= 1 << i; // x 不在树状数组范围内，或扩展失败
        else sum += C[x];
    }
    return x + 1;
}

简介线段树

“线段树”只是 Segment Tree 的一种称法，因为线段树可以理解为是由很多线段组成的，其它叫法包括区间树（interval tree）、范围树等等。但这些称法一般用于特殊领域（如计算几何），本文均用线段树来代表 Segment Tree。

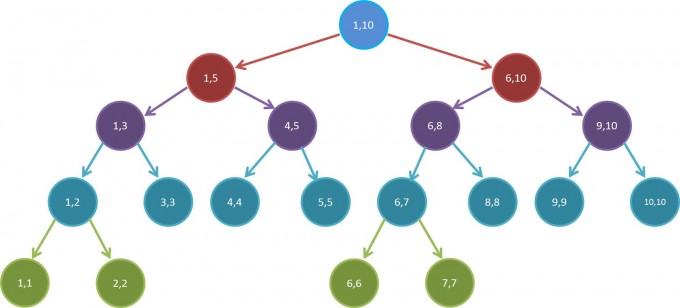
线段树是一种基于分治思想的二叉树结构，有如下特征：

线段树的每一个节点都代表一个区间。
线段树具有唯一的根节点，代表统计范围，一般为 $[1,n]$ 。
线段树的每个叶子节点长度都为 $1$ ，形如 $[x,x]$ 。
一般我们定义，若 $mid=\lfloor(l+r)\div2\rfloor$ ，那么节点 $[l,r]$ 的左子节点是 $[l,mid]$ ，右子节点是 $[mid+1,r]$ 。

一棵线段树

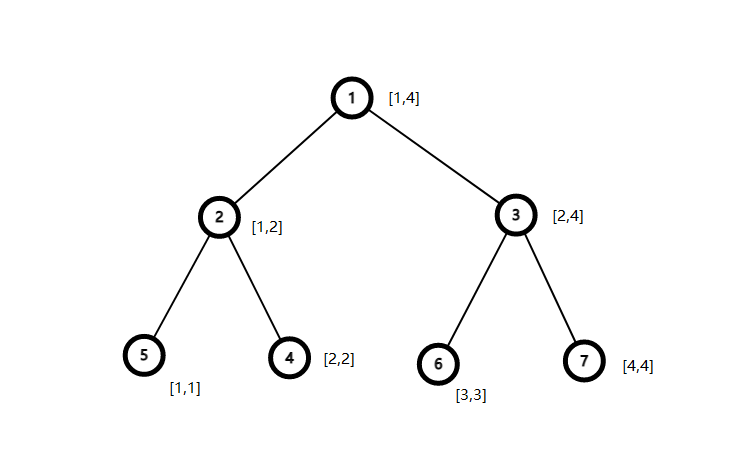
对于上图这棵维护区间 $[1,4]$ 的线段树而言，可以发现，一个节点的左子节点是它的编号乘 $2$ ，右子节点是乘 $2$ 加 $1$ 。我们可以利用这点方便地来存储线段树。

但凑巧的是，这颗线段树是满二叉树，其它情况类似于这种：

另一棵线段树

其实去掉最后一层这树仍是满二叉树，这种情况依然可以使用上述方法存树。

线段树的存储

线段树的正常写法是堆式线段树。

其实就是只用一个数组 $T$ 存储线段树，用堆的编号来表示线段树的左儿子和右儿子（lc = o << 1, rc = o << 1 | 1），不过进行操作的时候要多传两个数据 $l$ 和 $r$ 。

注意，线段树的节点必须开四倍空间！否则如果遇到非满二叉树的线段树，二倍空间就会爆炸！

在网上你能看到这样一种堆式线段树：

struct N {
    int l, r;
    int val;
} T[4*MAXN];

注意，它是记录了当前节点 $o$ 的区间 $[l,r]$ ，在传参时可以省掉两个参数（听不懂？那就不管，往下看就行）。
有时候要维护的信息特别复杂，我们会将数组 $T$ 的类型改为结构体，但还是不会使用记录区间的方式。

一般我们使用堆式线段树中的数组方式，而不记录左右儿子（不记慢不了多少）。接下来若不是特殊情况，我们均使用这种方式。

线段树的建树

接下来我们谈谈如何建树，我们再来看这棵线段树：

嘻嘻，还是我

最后一层若当作原序列的值，即 $[i,i]$ 保存 $A_i$ 的值。由于线段树是二叉树结构，可以很方便地从下往上传递信息。以区间和为例，令节点 $[l,r]$ 表示 $\sum\limits_{i=l}^{r}A_i$ ，显然 $[l,r]=[l,mid]+[mid+1,r]$ （这里的区间代表区间所对应的值）。

比如原序列是 1 2 3 4，那么对于节点 $1$ ~ $7$ ，可推算出它们的值分别为 10 3 7 1 2 3 4。

那么建树的代码大概就像这样：

#define L(x) ((x)<<1)
#define R(x) ((x)<<1|1)

// 当然，你也可以不用宏定义。

int T[4*N];

inline void maintain(int o) {
    T[o] = T[o << 1] + T[o << 1 | 1];
    // 从下往上传递信息。事实上你也可以写在需要调用 maintain 函数的函数里，不过有时传递的信息较为复杂，还是建议写一个 maintain 函数。网上有的教程把它写作 pushup，至于为什么，接下来你了解到 pushdown 就知道了。
}

void build(int o, int l, int r) { //o 代表当前维护结点的标号，l 和 r 代表所对应的区间
    if (l == r) return T[o] = a[l], void(); //如果这是叶子节点，赋值
    int mid = l + r >> 1; // 计算中值
    build(o << 1, l, mid); // 为左半段建树
    build(o << 1 | 1, mid + 1, r); // 为右半段建树
    maintain(o); // 计算当前结点的值
}

在 main 用 build(1, 1, n) 来调用 build。
由于每个节点只访问了一次，所以建树的时间复杂度为 $\mathcal{O}(n)$ 。

点修改与区间查询

模板。

点修改

还是以这棵线段树为例：

我又来啦

根据刚才的数据，初始化后它应该长这样：

初始化后的线段树

我们先来进行点修改，比如要给原序列的第 $2$ 个元素加上 $1$ ，那么这棵线段树会怎么变化呢？
可以发现，节点 $4$ 、 $2$ 、 $1$ 都会加上 $1$ 。线段树就变成了这个样子：

点修改后的线段树

那代码怎么实现呢？一般来讲，根节点 $1$ 总是线段树执行的入口，从根节点出发，递归找到需要修改的叶子节点，这里代码如下：

void update(int o, int l, int r, int x, int k) { //给原序列第 x 个元素加上 k。
    if (l == r) return T[o] += k, void(); // 这是叶子节点，直接加
    int mid = l + r >> 1;
    if (x <= mid) update(o << 1, l, mid, x, k); // 叶子节点在 [l,mid] 处。
    else update(o << 1 | 1, mid+1, r, x, k); // 叶子节点在 [mid+1,r] 处。
    maintain(o); //重新计算这个节点的值。
}

由于线段树的层数在 $\log$ 级别，所以点修改的时间复杂度为 $\mathcal{O}(\log n)$ 。

区间查询

查询区间 $[l,r]$ 的和，从根节点开始，递归执行下列过程：

若当前区间 $[l,r]$ 完全覆盖了需要求解的范围，那么直接返回答案。
若当前区间与左子节点有重叠，访问左子节点 $[l,mid]$ 。
若当前区间与右子节点有重叠，访问右子节点 $[mid+1,r]$ （注意不是访问左子节点后就不用访问右子节点了）。

那怎么解释这个东西呢？还是看那棵线段树 ~~（它的出镜率为什么这么高）~~：

嗯，又是我

比如现在我们要查 $[1,3]$ 。
$[1,3]$ 与 $[1,2]$ 和 $[3,4]$ 都有重叠，所以我们要分别访问。
$[1,2]$ 完全覆盖，直接返回。
$[3,4]$ 左子节点有覆盖，右子节点没有，访问左子节点。
$[3,3]$ 直接返回。
所以答案是 $4+3=7$ 。

那么代码就长这样：

int query(int o, int l, int r, int ql, int qr) { //[ql,qr] 是要查的区间
    if (ql <= l && r <= qr) return T[o]; //完全包含
    int mid = l + r >> 1, res = 0;
    // 接下来，只要你在（哪怕只有一个元素），我就查
    if (ql <= mid) res += query(o << 1, l, mid, ql, qr); //左子节点
    if (mid < qr) res += query(o << 1 | 1, mid+1, r, ql, qr); //右子节点
    return res;
}

同 update，query 的时间复杂度也是 $\mathcal{O}(\log n)$ 。

以下代码就可以通过刚才的模板了。

查看代码

#include <bits/stdc++.h>
using namespace std;

inline int read(void) {
    int x = 0, c = getchar(), f = 1;
    while (!isdigit(c)) {if (c == '-') f = -1; c = getchar();}
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x * f;
}

int n, m;
int T[2000005];
int a[500005];

void build(int o, int l, int r) {
    if (l == r) return T[o] = a[l], void();
    int mid = l + r >> 1;
    build(o << 1, l, mid);
    build(o << 1 | 1, mid+1, r);
    T[o] = T[o << 1] + T[o << 1 | 1];
}

void update(int o, int l, int r, int x, int k) {
    if (l == r) return T[o] += k, void();
    int mid = l + r >> 1;
    if (x <= mid) update(o << 1, l, mid, x, k);
    else update(o << 1 | 1, mid+1, r, x, k);
    T[o] = T[o << 1] + T[o << 1 | 1];
}

int query(int o, int l, int r, int ql, int qr) {
    if (ql <= l && r <= qr) return T[o];
    int mid = l + r >> 1, res = 0;
    if (ql <= mid) res += query(o << 1, l, mid, ql, qr);
    if (mid < qr) res += query(o << 1 | 1, mid+1, r, ql, qr);
    return res;
}

int main(void) {
    n = read(), m = read();
    for (int i = 1; i <= n; ++i) a[i] = read();
    build(1, 1, n);
    while (m--) {
        int op = read(), x = read(), y = read();
        if (op == 1) update(1, 1, n, x, y);
        else printf("%d\n", query(1, 1, n, x, y));
    }
    return 0;
}

Problemset

在讨论区间修改之前，我们先看几道线段树的题目。

基于线段树和树状数组的序列维护

树状数组

概述

线性建树

差分与前缀和

权值树状数组

树状数组二分与倍增

简介线段树

线段树的存储

线段树的建树

点修改与区间查询

点修改

区间查询

Problemset

[Luogu P4513] 小白逛公园

[UVa 1400] “Ray, Pass me the dishes!”

区间 GCD

区间修改与延迟标记

延迟标记的介绍

多组延迟标记

[UVa 11992] Fast Matrix Operations

[AHOI2009] 维护序列

线段树的本质

区间可加性

延迟标记与其它

权值线段树

动态开点线段树

线段树二分

线段树的分裂与合并

线段树合并

线段树分裂

Problemset

简单问题

[Luogu P1438] 无聊的数列

[Luogu P6327] 区间加区间 sin 和

「Wdsr-2.7」文文的摄影布置

[NOIP2016 提高组] 蚯蚓

[SDOI2009] HH 的项链

[GZOI2017] 配对统计

「Wdsr-3」令人感伤的红雨

技巧性问题

[Luogu P4145] 上帝造题的七分钟 2 / 花神游历各国

[TJOI2018] 数学计算

[SHOI2015] 脑洞治疗仪

[THUSC2015] 平方运算

综合应用

[HEOI2016] 排序

[Luogu P5278] 算术天才⑨与等差数列

[Luogu P6617] 查找 Search

[BJOI2019] 删数

[GDOI2014] 吃

[CTT2012] 序列操作

[Ynoi2015] 纵使日薄西山

[Code+#1] Yazid 的新生舞会

[RC-03] 记忆

[省选联考 2020 A/B 卷] 冰火战士

[CF187D] BRT Contract

线段树分裂与合并

[POI2011] ROT-Tree Rotations

[湖南集训] 更为厉害

[NOI2020] 命运