二叉搜索树与平衡树

二叉搜索树（Binary Search Tree, BST）是一种二叉树的树形数据结构，能高效地解决许多其它数据结构所不能解决的问题，但由于自身是一个不稳定，容易退化的数据结构，所以需要用特殊手段保证其平衡。

更新日志

2023/10/12

完成预定所有内容。

概念

二叉树有一种性质叫做二叉搜索树性质，就是说对于树中的一个节点，它的键值不小于它左子树的键值，不大于它右子树的键值，这就是所谓的“BST 性质”。

BST 的递归定义如下：

空树是 BST；
若 BST 的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值；
若 BST 的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值；
BST 的左右子树均为 BST；
BST 集合是满足 1、2、3、4 的最小二叉树集。

所以输出 BST 的中序遍历就是原序列排序的结果。

需要注意的是，一般的，BST 所有节点的键值都不相等。

普通 BST

模板。

您需要写一种数据结构，来维护一些数（都是 $10^9$ 以内的数字）的集合，最开始时集合是空的。其中需要提供以下操作，操作次数 $q$ 不超过 $10^4$ ：

查询 $x$ 数的排名（排名定义为比当前数小的数的个数 $+1$ 。若有多个相同的数，应输出最小的排名）。
查询排名为 $x$ 的数。
求 $x$ 的前驱（前驱定义为小于 $x$ ，且最大的数）。若未找到则输出 $-2147483647$ 。
求 $x$ 的后继（后继定义为大于 $x$ ，且最小的数）。若未找到则输出 $2147483647$ 。
插入一个数 $x$ 。

BST 的节点会这样定义：

struct Node {
    int l, r; // 左右儿子
    int val; // 键值
    int cnt, size; // 表示这个节点数个个数，和子树的大小
}T[maxn];

辅助函数如下：

int tot = 0;
inline int newNode(int val) // 新建节点，并返回编号
{
    T[++tot] = val;
    T[tot].size = T[tot].cnt = 1;
    return tot;
}
inline void maintain(int p) { // 维护当前节点的信息
    T[p].size = T[T[p].l].size + T[T[p].r].size + T[p].cnt;
}

为了使边界处理情况更为方便，我们会插入一个 INF 节点和一个 -INF 节点，这样建树：

int root = 1; // 定义根节点，必须这么做的原因是在平衡树中会出现树根改变的情况
const int INF = 2147483647; // 定义 INF
void build(void) {
    newNode(-INF), newNode(INF);
    root = 1, T[1].r = 2;
}

求排名：

int Rank(int p, int val) {
    if (p == 0) return 1;
    // 只有在此 val 不存在时才会访问到 0 号节点，根据定义，排名应该 +1，所以返回 1。
    // 在不同情况下这里会返回不同的值，比如如果次数不存在输出 -1 这里就应该返回 ERROR_BAD_USAGE，若数不存在就不用 +1，则返回 0。
    if (val == T[p].val) return T[T[p].l].size + 1; // 找到节点，返回
    if (val < T[p].val) return Rank(T[p].l, val); // 小，在左子树中找
    return Rank(T[p].r, val) + T[T[p].l].size + T[p].cnt; // 大，右子树找，注意要加上左子树和此节点
}

求排名为 $k$ 的数：

int kth(int p, int rnk) {
    if (p == 0) return INF; // 0 意味着当前树上的节点数小于 rnk，返回 INF
    if (T[T[p].l].size >= rnk) return kth(T[p].l, rnk); // 在左子节点
    if (T[T[p].l].size + T[p].num >= rnk) return T[p].val; // 当前节点
    return kth(T[p].r, rnk - T[T[p].l].size - T[p].cnt); // 右子节点
}

怎么查前驱呢？初始 ans = 1，检索 val，有三种可能的结果：

BST 中没有 val。后继一定在已经遍历的节点中，这一点可以用微扰来证明。
有 val 节点，但是这个节点没有右子树。这种情况的答案同 1。
有 val 节点，有右子树。答案是右子树的最低端。

代码（请读者自行实现后继）：

inline int GetPre(int val) {
    int ans = 1, p = root; // T[1].val == -INF
    while (p) {
        if (val == T[p].val) {
            if (T[p].l) { // 存在左子节点
                p = T[p].l;
                while (T[p].r) p = T[p].r; // 使劲往右走
                ans = p;
            }
            break;
        }
        if (T[p].val < val && T[p].val > T[ans].val) ans = p; // 尝试更新 ans
        p = val < T[p].val ? T[p].l : T[p].r; // 遍历
    }
    return T[ans].val;
}

当然前驱和后继也可以直接使用 Rank 和 kth 函数实现，大概像这样：

kth(root, Rank(root, x) - 1) // 前驱
kth(root, Rank(root, x) + 1) // 后继，但是应该写成 kth(root, Rank(root, x + 1))

由于这里是严格大于和严格小于，所以说排名不能简单地写成 +1，边界条件非常容易写错，所以还是推荐大家来写前驱后继函数。也可以以采用递归的形式：

int GetPre(int p, int k) {
    if (!p) return -INF;
    if (T[p].val >= k) return GetPre(T[p].ch[0], k);
    return max(T[p].val, GetPre(T[p].ch[1], k));
}

插入的代码非常好写：

void insert(int &p, int val) // p 是父亲节点
{
    if (p == 0) return p = newNode(val), void();
    if (val == T[p].val) { // 有这一键值
        ++T[p].cnt; // 将个数加上 1
        maintain(p);
        return;
    }
    // 接下来看它是在左子树还是在右子树
    if (val < T[p].val) insert(T[p].l, val); // 根据 BST 的定义，在左子树
    else insert(T[p].r, val); // 在右子树
    maintain(p); // 由于进行了插入，当前节点的信息需要重新计算
}

注意我们在有这一键值的时候并没有重新计算父亲节点，因为插入是递归进行的，父亲节点的附加信息一定会被重新计算。

平衡 BST

但是这样的 BST 的时间复杂度是假的，因为如果插入 1 2 3 4 5 6 7，它就会变成一条链。

简介

表达同种意思的 BST 有多种，有平衡的，有不平衡的。在数据随机的情况下，它就是平衡的。不平衡怎么办？给他搞成平衡的呗。

那为什么平衡树有快有慢呢？这是因为，越快的平衡树能使平衡树越满。但有些平衡树实现过于复杂，比如红黑树（Red-Black Tree，简称 RBT），它的插入有 $5$ 种情况，删除有 $6$ 种情况，在考场上根本打不出来（当然工程中你必须打），所以一般情况下我们不使用红黑树。

但要注意的是，尽量不要在考场手写上写平衡树。若 STL 能满足要求，就使用 STL。STL 的红黑树开了 O2 以后，跑得比大多数手写平衡树都要快（不信你可以学完平衡树后自己实现一个山寨版的 set 来和 STL 比比速度）。尽量不要自己再造轮子，造不好就被碾着腿了。

在工程中，常用的平衡树是 AVL、RBT 和 B 树（B 树不是二叉树，而是多叉的）；而在竞赛中，常用的则是 Treap 和 Splay（伸展树）。当然还有诸如 WBLT，替罪羊树等平衡树。本文会介绍旋转 Treap、Splay 和非旋 Treap（FHQ-Treap）。

平衡的思路

有三种：旋转，分裂与合并，重构。
但它们的目的都是相同的：平衡我们的二叉搜索树。

对于旋转，有单旋转和双旋转。单旋指一个节点和它的父亲转，双旋还会涉及到它的爷爷。

下面将介绍几种最为常用的平衡树。

Treap

这是一种最基础的平衡树，代码与普通的二叉搜索树差不了多少。但如果要实现名次树，它的速度是非常快的（OI 中常用的平衡树中最快）。
接下来我们要用 Treap 实现名次树（因为所有操作都是围绕排名来进行的，所以叫做名次树），模板。

原理

Treap 是一种弱平衡 BST（是指不会为了把自己搞成除了最后一层不是满的二叉树而过多的变换自己的形态，AVL 便是严格平衡树），它是一个合成词，有 Treap = Tree + Heap，所以 Treap 又叫做树堆（怎么听上去那么搞笑）。

Treap 有两种形式，无旋式有旋转式。无旋式能做到快速分裂与合并，就是 FHQ-Treap。

回到刚才所说的树堆中。Treap 除了节点的权值满足二叉搜索树性质以外，它的附加权值还满足堆性质（这里统一为大根堆性质）。这样就可以证明如果每个节点的附加权值全不同，那么 Treap 的形态是唯一的（但不一样也不影响我们干活）。

普通的 BST 在随机情况下就是平衡的。Treap 通过人为制造随机，随机赋予节点的附加权值。由于堆是一棵完全二叉树，所以 Treap 是期望平衡的，单次操作期望复杂度 $O(\log n)$ 。

理论上应该没有毒瘤来卡你。

关键是旋转，怎么转？可以看这张图：

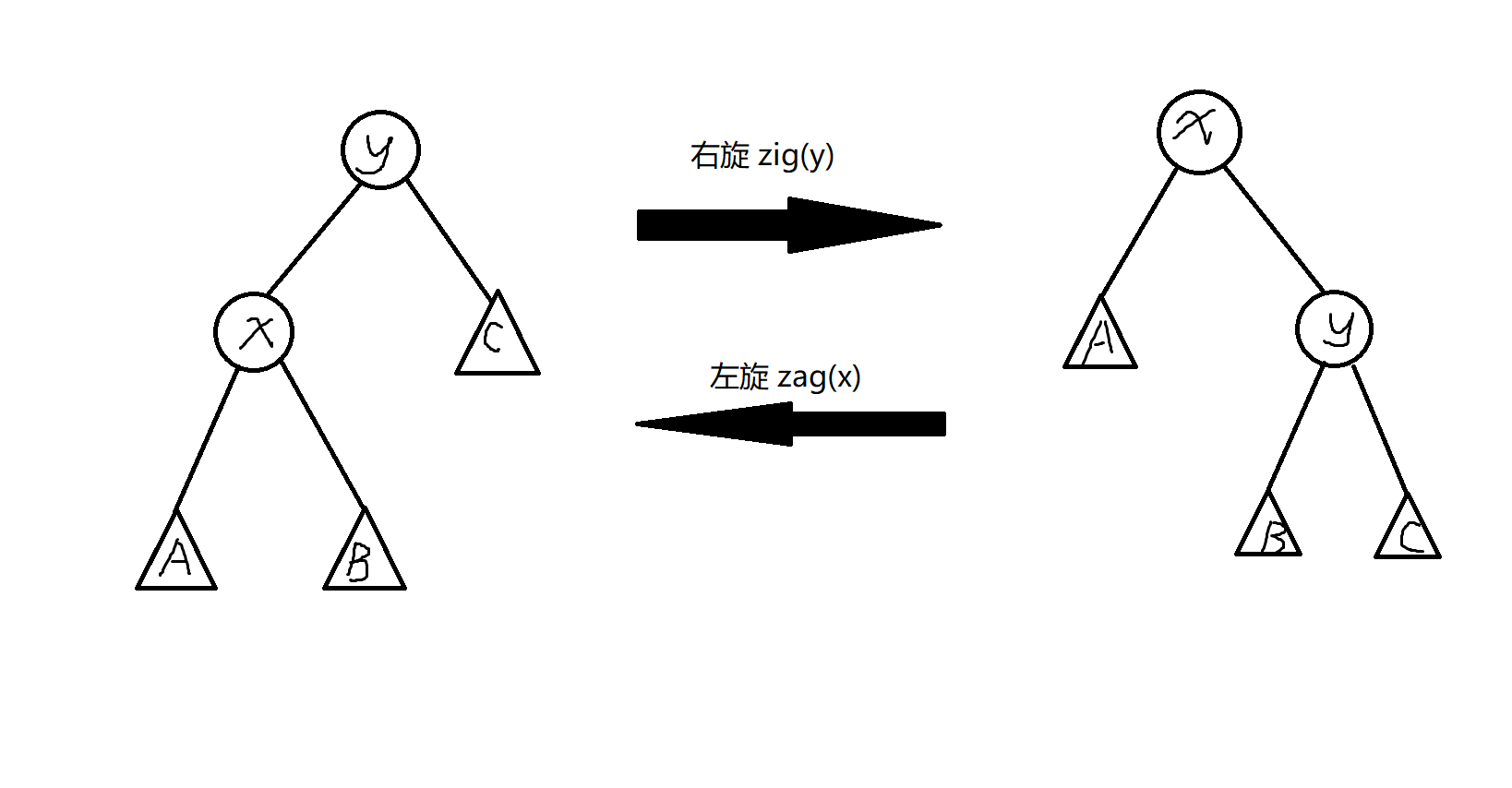
zig(y) 代表 y 旋转前处于父亲节点，然后右旋至它的右子节点；zag(x) 是左旋，旋转到它的左子节点。圆形代表节点，三角代表子树。

当 $y$ 右旋时，它会移到它的右子节点的位置，将他它左子节点 $x$ 移到它原来的位置，而由于 $x$ 的右子树 $B$ 不能再属于 $x$ 了，而根据 BST 的定义， $B<y$ ，所以 $B$ 变成了 $y$ 的左子树。另外，当旋转之后， $x$ 和 $y$ 的附加信息都需要重新计算，而且 $y$ 是 $x$ 的儿子，所以先维护 $y$ 再维护 $x$ 。

左旋类似，这里留给读者自己撕烤。

实现

接下来我们要干一件大事：推翻我们以前 BST 的写法。

为什么？因为它实在是太容易出错了。如果你感觉很难接受，没关系，在文中我们还会介绍各种写法及其优劣。

首先是节点的定义，像这样：

struct Node {
    int ch[2]; // 左右儿子的编号
    int val, dat; // 键值和随机权值
    int size, cnt; // 子树大小和此节点的值的个数
}T[maxn];

可以发现变化是将左右儿子和到了一起。这是为了方便实现旋转。更加激进的写法是:

struct Node {
    Node *ch[2]; // 左右儿子
    int val, dat;
    int size, cnt;
};

看见什么了？指针？的确如此。这种方法的好处多多，第一会使你的代码更加流畅，不会出现数组套数组的窘况。二是会节省一些内存。但考虑到竞赛中不要使用指针的基本原则（虽然工程中这种写法是必备的），接下来的代码统一采用数组伪指针的形式。

实际上还有另一种记录节点的方式，就是多记录每个节点的父亲。虽然这种做法在下文要介绍的伸展树中比较常见，但在 Treap 中，它的优点是旋转时可以更自然的对一个节点进行旋转，而不是在函数调用中写先定义好的父亲。如果你想学习这种写法，学完接下来介绍的 Splay 后你就可以给它迁移过来辣！

首先是一些基本定义，如下：

Node T[100005];
int tot;
inline void maintain(int p) { T[p].size = T[T[p].ch[0]].size + T[T[p].ch[1]].size + T[p].cnt; }
inline int newNode(int val)
{
    T[++tot].val = val;
    T[tot].dat = rand();
    T[tot].size = T[tot].cnt = 1;
    return tot;
}

唯一值得注意的是 dat 值的设置，随机一个数即可。

然后是旋转。旋转的原理已经了解过了，这里再次放出那张图，然后直接阅读下面的代码（同时进行手动模拟，对着每个节点转，就是改变这个节点的信息，不要对着图中的位置转）：

zig(y) 代表 y 旋转前处于父亲节点，然后右旋至它的右子节点；zag(x) 是左旋，旋转到它的左子节点。圆形代表节点，三角代表子树。

inline void rotate(int &p, int d) // 绕着 p 点旋转，d = 0 左旋，d = 1 右旋，d^1 = 1-d
{
    int q = T[p].ch[d^1]; // 找到 p 的儿子，这个儿子将要旋转到根上
    T[p].ch[d^1] = T[q].ch[d]; // 接下自己的儿子要丢的儿子，因为自己要变成自己的儿子的儿子了
    T[q].ch[d] = p; // 原来儿子的儿子设为原来的爸爸
    p = q; // 原来的儿子正式登上爸爸的宝座，注意 p 是引用
    maintain(T[p].ch[d]), maintain(p); // 从下到上重新计算附加信息
}

注意某些节点旋转后，附加节点的信息就必须重新计算，而且要注意计算顺序。但某些文章你会看到类似这样的旋转：

inline void zig(int &p) // 右旋
{
    int q = T[p].l;
    T[p].l = T[q].r, T[q].r = p, p = q;
    maintain(T[p].r), maintain(p);
}
inline void zag(int &p) // 左旋
{
    int q = T[p].r;
    T[p].r = T[q].l, T[q].l = p, p = q;
    maintain(T[p].l), maintain(p);
}

这也是对的，但是把一个函数就能完成的内容拆到两个函数里实属麻烦，而且到后来你会发现，zig zag 就是个屎坑，千万别跳，千万别跳，千万别跳，三体警告。

然后是插入操作，只需要在不符合堆性质的时候进行旋转维护堆性质即可，代码如下：

void insert(int &p, int val)
{
    if (p == 0) // 此节点不存在，直接新建
    {
        p = newNode(val);
        return;
    }
    if (val == T[p].val) ++T[p].cnt; // 存在这一键值，计数 +1
    else
    {
        // 这种方式能极大地简化代码
        int d = (val < T[p].val ? 0 : 1);
        insert(T[p].ch[d], val);
        if (T[T[p].ch[d]].dat > T[p].dat) rotate(p, d^1); // 不符合堆性质，儿子比父亲大，将儿子转到父亲的位置上
    }
    maintain(p);
}

常规的 Rank kth GetPre GetNext 操作和普通 BST 没有什么区别，留给读者自行实现。

最后是 Remove 操作。为什么普通 BST 没有 Remove 操作呢？因为 Remove 操作意味着对二叉搜索树性质的复杂维护。但是 Treap 不一样，它支持旋转。我们只需要把要删除的节点转成叶子节点，然后直接删除即可。代码如下：

void Remove(int &p, int val)
{
    if (p == 0) return;
    if (T[p].val == val)
    {
        if (T[p].cnt > 1) // 这个节点多于 1
        {
            --T[p].cnt;
            maintain(p);
            return;
        }
        if (T[p].ch[0] || T[p].ch[1])
        {
            int d = (T[p].ch[1] == 0 || T[T[p].ch[0]].dat > T[T[p].ch[1]].dat) ? 1 : 0; // 维护大根堆性质的前提下选择转到哪个方向
            rotate(p, d); // 将要删除的节点 p 转到儿子的位置上
            Remove(T[p].ch[d], val);
            maintain(p); // 此时节点的附加信息要重新计算
        }
        else p = 0; // 叶子节点直接删除
        return;
    }
    Remove(T[p].ch[val < T[p].val ? 0 : 1], val); // 递归删除
    maintain(p);
}

合并后代码如下：

查看代码

#include <bits/stdc++.h>
using namespace std;

const int INF = 2147483647;

inline int read(void)
{
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

struct Node
{
    int ch[2];
    int val, dat;
    int size, cnt;
};

class Treap
{
    private:
        Node T[1100005];
        int tot;
        inline void maintain(int p) { T[p].size = T[T[p].ch[0]].size + T[T[p].ch[1]].size + T[p].cnt; }
        inline int newNode(int val)
        {
            T[++tot].val = val;
            T[tot].dat = rand();
            T[tot].size = T[tot].cnt = 1;
            return tot;
        }
        inline void rotate(int &p, int d)
        {
            int q = T[p].ch[d^1];
            T[p].ch[d^1] = T[q].ch[d], T[q].ch[d] = p, p = q;
            maintain(T[p].ch[d]), maintain(p);
        }
    public:
        int root;
        inline void build(void)
        {
            srand(time(0)); // 不写这个，小心毒瘤 Hack 你
            newNode(-INF), newNode(INF);
            T[1].ch[1] = 2, root = 1;
            maintain(root);
        }
        void insert(int &p, int val)
        {
            if (p == 0)
            {
                p = newNode(val);
                return;
            }
            if (val == T[p].val) ++T[p].cnt;
            else
            {
                int d = (val < T[p].val ? 0 : 1);
                insert(T[p].ch[d], val);
                if (T[T[p].ch[d]].dat > T[p].dat) rotate(p, d^1);
            }
            maintain(p);
        }
        int Rank(int p, int val)
        {
            if (p == 0) return 1;
            if (val == T[p].val) return T[T[p].ch[0]].size + 1;
            if (val < T[p].val) return Rank(T[p].ch[0], val);
            return Rank(T[p].ch[1], val) + T[T[p].ch[0]].size + T[p].cnt;
        }
        int kth(int p, int rnk)
        {
            if (p == 0) return INF;
            if (rnk <= T[T[p].ch[0]].size) return kth(T[p].ch[0], rnk);
            if (rnk <= T[T[p].ch[0]].size + T[p].cnt) return T[p].val;
            return kth(T[p].ch[1], rnk - T[T[p].ch[0]].size - T[p].cnt);
        }
        inline int GetPre(int val)
        {
            int ans = 1, p = root;
            while (p)
            {
                if (val == T[p].val)
                {
                    if (T[p].ch[0])
                    {
                        p = T[p].ch[0];
                        while (T[p].ch[1]) p = T[p].ch[1];
                        ans = p;
                    }
                    break;
                }
                if (T[p].val < val && T[p].val > T[ans].val) ans = p;
                p = T[p].ch[val < T[p].val ? 0 : 1];
            }
            return T[ans].val;
        }
        inline int GetNext(int val)
        {
            int ans = 2, p = root;
            while (p)
            {
                if (val == T[p].val)
                {
                    if (T[p].ch[1])
                    {
                        p = T[p].ch[1];
                        while (T[p].ch[0]) p = T[p].ch[0];
                        ans = p;
                    }
                    break;
                }
                if (T[p].val > val && T[p].val < T[ans].val) ans = p;
                p = T[p].ch[val < T[p].val ? 0 : 1];
            }
            return T[ans].val;
        }
        inline void Remove(int &p, int val)
        {
            if (p == 0) return;
            if (T[p].val == val)
            {
                if (T[p].cnt > 1)
                {
                    --T[p].cnt;
                    maintain(p);
                    return;
                }
                if (T[p].ch[0] || T[p].ch[1])
                {
                    int d = (T[p].ch[1] == 0 || T[T[p].ch[0]].dat > T[T[p].ch[1]].dat) ? 1 : 0;
                    rotate(p, d); Remove(T[p].ch[d], val);
                    maintain(p);
                }
                else p = 0;
                return;
            }
            Remove(T[p].ch[val < T[p].val ? 0 : 1], val);
            maintain(p);
        }
}T;

int main(void)
{
    int n = read(), m = read();
    T.build();
    while (n--) T.insert(T.root, read());
    int ans = 0, last = 0;
    while (m--)
    {
        int opt = read(), x = read();
        x ^= last;
        if (opt == 1) T.insert(T.root, x);
        else if (opt == 2) T.Remove(T.root, x);
        else if (opt == 3) last = T.Rank(T.root, x) - 1;
        else if (opt == 4) last = T.kth(T.root, x + 1);
        else if (opt == 5) last = T.GetPre(x);
        else last = T.GetNext(x);
        if (opt > 2) ans ^= last;
    }
    printf("%d\n", ans);
    return 0;
}

FHQ-Treap

正常的 Treap 并不支持分裂与合并，但是由范浩强提出的无旋 Treap 可以快速地分裂与合并，实现 Splay 的大部分功能，而且效率比 Splay 高很多。

这种平衡树甚至被称为“最好写的平衡树”，情况远远没有 Splay 那么复杂。

实现

所有 Treap 的基本模板都适用，但是要注意，我们不再记录一个 $val$ 出现的次数 $cnt$ ，因为基于分裂与合并实现的平衡树没办法简单的实现找的一个节点的位置。但是不用担心，即使不记录 $cnt$ ，树中的节点键值可以重复，它依然可以正常工作。

struct Node {
	int ch[2];
	int size;
	int val, dat;
} T[1100005];
int tot = 0;
inline void maintain(int p) { T[p].size = T[T[p].ch[0]].size + T[T[p].ch[1]].size + 1; }
inline int newNode(int val) {
	T[++tot].val = val;
	T[tot].dat = rand(), T[tot].size = 1;
	return tot;
}
int main(void) { srand(time(0)); }

分裂与合并

由于 FHQ 并不支持旋转，所以一切维护平衡的手段都依赖于分裂与合并，其时间复杂度均为 $O(\log n)$ 。

什么是平衡树的分裂与合并呢？简单地说，之前的平衡树之能有一个根，但是现在可以有多个。由于 BST 的递归性质，所以可以很方便地合并两个 BST。

分裂

按 val 分裂。按照键值 val 将 Treap 分裂成两棵子树，其中一棵树 $x$ 的值全部小于等于 $val$ ，剩下的是另外一棵 $y$ 全部大于 $val$ 的。

函数定义为 split(p, key, x, y)，代表遍历到 $p$ ，根据 $key$ 作为键值分裂成两棵子树 $x,y$ 。具体怎么做呢？

如果 $val[p]\le key$ ，那么应该被放到 $x$ 上，否则被放到 $y$ 上。而放在子树中的具体哪一个位置？很显然需要递归进行。

void split(int p, int key, int &x, int &y) {
	if (!p) return x = y = 0, void(); // 空了，分裂之后都是 0
	if (T[p].val <= key) { // p 应该被分裂到 x 上
		x = p; // 让 p 作为 x 的根，现在左子树全归 x 了
		split(T[p].ch[1], key, T[p].ch[1], y); // 开始分裂右子树，右子树中有 <= key 的应该给 x 的右子树
	} else {
		y = p;
    	split(T[p].ch[0], key, x, T[p].ch[0]);
    }
    maintain(p); // 当前节点的信息需要重新计算
}

按 size 分裂。按照子树的大小，前 $siz$ 给 $x$ ，剩余的给 $y$ ，也很容易实现。

void split(int p, int siz, int &x, int &y) {
	if (!p) return x = y = 0, void();
	if (T[T[p].ch[0]].size + 1 <= siz) { // p 应该被分裂到 x 上
		x = p; // 让 p 作为 x 的根，现在左子树全归 x 了
		split(T[p].ch[1], siz - T[T[p].ch[0]].size - 1, T[p].ch[1], y); // 开始分裂右子树，右子树中应有 siz - p->l->size - 1 归 x
	} else {
		y = p;
    	split(T[p].ch[0], siz, x, T[p].ch[0]);
    }
    maintain(p);
}

合并

合并的时候显然要求 $x$ 中的每一个节点都小于 $y$ 中的每一个节点，然后根据 Treap 的堆性质来判断是将 $x$ 合并到 $y$ 还是将 $y$ 合并到 $x$ 。

int merge(int x, int y) // 要求 x 中的每一个节点都小于 y 中的每一个节点
{
    if (x == 0 || y == 0) return x + y; // 有一棵是空的，那么返回另一棵
    if (T[x].dat > T[y].dat) // 需要维护大根堆性质，将 y 合并到 x
    {
        T[x].ch[1] = merge(T[x].ch[1], y);
        maintain(x);
        return x;
    }
    else
    {
        T[y].ch[0] = merge(x, T[y].ch[0]);
        maintain(y);
        return y;
    }
}

实现名次树

分裂与合并是 FHQ-Treap 的核心操作，剩下的所有操作都基于分裂与合并。

插入

将 $key$ 分裂出来，然后合并三次即可。

void insert(int key)
{
    int x, y;
    split(root, key - 1, x, y); // 到时候 val 的左子节点是 x，右子节点是 y
    root = merge(merge(x, newNode(key)), y);
}

删除

分裂两次将 $key$ 分裂出来，然后进行删除。

void Remove(int key)
{
    // 将 root 按照 key 分裂成 x, z
    // 将 x 按照 key - 1 分裂成 x, y
    // 这时 x < key, y = key, z > key
    // y 中的只需要删一个
    // 如果删去所有的，那么合并时直接 root = merge(x, z)
    int x, y, z;
    split(root, key, x, z);
    split(x, key - 1, x, y);
    if (y) y = merge(T[y].ch[0], T[y].ch[1]); 
    root = merge(merge(x, y), z);
}

求排名

将 $key$ 分裂出来，然后就是 $x$ 树的大小 +1 了。

int Rank(int key)
{
    int x, y, ans;
    split(root, key - 1, x, y);
    ans = T[x].size + 1; // 排名等于 < key 的个数 +1
    root = merge(x, y); // 再把它合并回去，还原现场
    return ans;
}

求 k 小

有两种方式，但是比较推荐类似于之前普通 BST 的方式。

另一种是利用基于大小的分裂，但是这样代码会变多。

前驱后继

对于前驱，将小于的分裂出来，然后再这棵树上尽可能往右走。后继大致同理。

int GetPre(int key)
{
    int x, y, p, ans;
    split(root, key - 1, x, y); // 找到小于等于的
    p = x;
    while (T[p].ch[1]) p = T[p].ch[1]; // 尽可能往右走
    ans = T[p].val; // 在还原现场之前先记录答案
    root = merge(x, y);
    return ans;
}

int GetNext(int key)
{
    int x, y, p, ans;
    split(root, key, x, y);
    p = y;
    while (T[p].ch[0]) p = T[p].ch[0];
    ans = T[p].val;
    root = merge(x, y);
    return ans;
}

性能

FHQ-Treap 通过平衡树模板的代码如下：

查看代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <ctime>

using namespace std;

struct Node {
    int ch[2], size;
	int val, dat;
} T[1100005];
int tot = 0, root;
inline void maintain(int p) { T[p].size = T[T[p].ch[0]].size + T[T[p].ch[1]].size + 1; }
inline int newNode(int val) {
	T[++tot].val = val;
	T[tot].dat = rand(), T[tot].size = 1;
	return tot;
}

void split(int p, int key, int &x, int &y) {
	if (!p) return x = y = 0, void();
	if (T[p].val <= key) {
		x = p;
		split(T[p].ch[1], key, T[p].ch[1], y);
	} else {
		y = p;
    	split(T[p].ch[0], key, x, T[p].ch[0]);
    }
    maintain(p);
}

int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y;
    if (T[x].dat > T[y].dat) {
        T[x].ch[1] = merge(T[x].ch[1], y); maintain(x);
        return x;
    } else {
        T[y].ch[0] = merge(x, T[y].ch[0]); maintain(y);
        return y;
    }
}

void insert(int key) {
    int x, y;
    split(root, key - 1, x, y);
    root = merge(merge(x, newNode(key)), y);
}

void Remove(int key) {
    int x, y, z;
    split(root, key, x, z);
    split(x, key - 1, x, y);
    if (y) y = merge(T[y].ch[0], T[y].ch[1]); 
    root = merge(merge(x, y), z);
}

int Rank(int key) {
    int x, y, ans;
    split(root, key - 1, x, y);
    ans = T[x].size + 1;
    root = merge(x, y);
    return ans;
}

int kth(int rnk) {
    int p = root;
    while (p) {
        if (T[T[p].ch[0]].size + 1 == rnk) break;
        else if (T[T[p].ch[0]].size + 1 > rnk) p = T[p].ch[0];
        else {
            rnk -= T[T[p].ch[0]].size + 1;
            p = T[p].ch[1];
        }
    }
    return T[p].val;
}

int GetPre(int key) {
    int x, y, p, ans;
    split(root, key - 1, x, y);
    p = x;
    while (T[p].ch[1]) p = T[p].ch[1];
    ans = T[p].val;
    root = merge(x, y);
    return ans;
}

int GetNext(int key) {
    int x, y, p, ans;
    split(root, key, x, y);
    p = y;
    while (T[p].ch[0]) p = T[p].ch[0];
    ans = T[p].val;
    root = merge(x, y);
    return ans;
}

int read(void) {
    int x = 0, c = getchar_unlocked();
    while (!isdigit(c)) c = getchar_unlocked();
    while (isdigit(c)) x = x * 10 + c - '0', c = getchar_unlocked();
    return x;
}

int main(void) {
    srand(time(0));
    int n = read(), m = read();
    while (n--) insert(read());
    int ans = 0, last = 0;
    while (m--) {
        int opt = read(), x = read();
        x ^= last;
        if (opt == 1) insert(x);
        else if (opt == 2) Remove(x);
        else if (opt == 3) last = Rank(x);
        else if (opt == 4) last = kth(x);
        else if (opt == 5) last = GetPre(x);
        else last = GetNext(x);
        if (opt > 2) ans ^= last;
    }
    printf("%d\n", ans);
    return 0;
}

测试性能之后发现，Treap 用时 9.78s，FHQ-Treap 用时 12.60s，FHQ 还是会慢一些，不过足够了。

正如我们所说，Treap 是 OI 范围内能用到的最快的平衡树，FHQ 结合了 Treap 的优点并且支持 Splay 的分裂与合并，是很棒的平衡树。

分裂与合并的序列

FHQ 可以用来实现 Splay 的快速分裂合并功能。

区间翻转

模板。

我们先看一下如何实现分裂与合并的序列：我们只需要把区间的下标依次插入 Treap 中，也就是我们不再利用二叉搜索树的性质，不再是根据权值而建立平衡树，只是利用了它们能够分裂与合并的特性，此时节点的键值只是表示序列中一个数的相应大小，而序列的顺序由 Treap 的中序遍历保证。

区间翻转的时候，我们按照大小分裂为 $[1,l-1],[l,r],[r+1,n]$ ，然后给中间的树打上一个 $rev$ 标记，代表是否将左右儿子翻转（由于中序遍历的性质，将左右儿子反转后的序列便是原序列），然后操作的时候要进行 pushdown。

查看代码

#include <iostream>
#include <cstdio>
#include <random>
#include <ctime>

using namespace std;

struct Node {
    int ch[2], siz, dat, id;
    bool rev;
} T[100005];
int tot = 0, root;
mt19937 Rand(time(0));
void maintain(int p) { T[p].siz = T[T[p].ch[0]].siz + T[T[p].ch[1]].siz + 1; }
int newNode(int id) {
    T[++tot].id = id; T[tot].dat = Rand(); T[tot].siz = 1;
    return tot;
}
void pushdown(int p) {
    if (!T[p].rev) return;
    swap(T[p].ch[0], T[p].ch[1]);
    T[T[p].ch[0]].rev ^= 1; T[T[p].ch[1]].rev ^= 1;
    T[p].rev = 0;
}
void print(int x) {
    if (!x) return; pushdown(x);
    print(T[x].ch[0]); printf("%d ", T[x].id); print(T[x].ch[1]);
}
void split(int p, int S, int &x, int &y) {
    if (!p) return x = y = 0, void(); pushdown(p);
    if (T[T[p].ch[0]].siz + 1 <= S) {
        x = p;
        split(T[p].ch[1], S - T[T[p].ch[0]].siz - 1, T[p].ch[1], y);
    } else {
        y = p;
        split(T[p].ch[0], S, x, T[p].ch[0]);
    }
    maintain(p);
}
int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y;
    if (T[x].dat > T[y].dat) {
        pushdown(x); T[x].ch[1] = merge(T[x].ch[1], y); maintain(x);
        return x;
    } else {
        pushdown(y); T[y].ch[0] = merge(x, T[y].ch[0]); maintain(y);
        return y;
    }
}
void update(int l, int r) {
    int x, y, z;
    split(root, l - 1, x, y);
    split(y, r - l + 1, y, z);
    T[y].rev ^= 1;
    root = merge(merge(x, y), z);
}

int n, m;
int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) root = merge(root, newNode(i));
    while (m--) {
        int l, r; scanf("%d%d", &l, &r);
        update(l, r);
    }
    print(root); putchar('\n');
    return 0;
}

一般序列操作

注意延迟标记的使用，大致是跟线段树一样的，覆盖当前节点的时候需要直接修改当前节点的相关信息。

再就是建树，采用类似于线段树的建树方式可以使合并的操作次数达到最少。

合理利用分裂与合并，将想要搞的信息直接分裂出来即可，合并可以合理安排序列的顺序。

模板，代码如下：

查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 500000;

mt19937 Rand(time(0));
struct Node {
    int ch[2], siz, rnd, val;
    int sum, lmax, rmax, dat;
    bool rev, setv;
} T[500005];
int st[500005], tot, root, a[500005];
int newNode(int val) {
    int p = st[tot--];
    T[p].rnd = Rand(); T[p].siz = 1;
    T[p].ch[0] = T[p].ch[1] = T[p].rev = T[p].setv = 0;
    T[p].val = T[p].sum = T[p].dat = val;
    T[p].lmax = T[p].rmax = max(val, 0);
    return p;
}
void maintain(int p) { 
    int l = T[p].ch[0], r = T[p].ch[1];
    T[p].siz = T[l].siz + T[r].siz + 1; 
    T[p].sum = T[l].sum + T[r].sum + T[p].val;
    T[p].lmax = max(T[l].lmax, T[l].sum + T[p].val + T[r].lmax);
    T[p].rmax = max(T[r].rmax, T[r].sum + T[p].val + T[l].rmax);
    T[p].dat = max(T[l].rmax + T[r].lmax, 0) + T[p].val;
    if (l) T[p].dat = max(T[p].dat, T[l].dat);
    if (r) T[p].dat = max(T[p].dat, T[r].dat);
}
void cover(int p, int k) {
    T[p].val = k; T[p].sum = k * T[p].siz;
    T[p].lmax = T[p].rmax = max(T[p].sum, 0);
    T[p].dat = max(T[p].sum, T[p].val);
    T[p].setv = 1; T[p].rev = 0;
}
void rever(int p) {
    swap(T[p].ch[0], T[p].ch[1]); swap(T[p].lmax, T[p].rmax);
    T[p].rev ^= 1;
}
void pushdown(int p) {
    if (!p) return;
    if (T[p].rev) {
        if (T[p].ch[0]) rever(T[p].ch[0]); 
        if (T[p].ch[1]) rever(T[p].ch[1]);
        T[p].rev = 0;
    }
    if (T[p].setv) {
        if (T[p].ch[0]) cover(T[p].ch[0], T[p].val); 
        if (T[p].ch[1]) cover(T[p].ch[1], T[p].val);
        T[p].setv = 0;
    }
}

void split(int p, int S, int &x, int &y) {
    if (!p) return x = y = 0, void(); pushdown(p);
    if (T[T[p].ch[0]].siz + 1 <= S) {
        x = p;
        split(T[p].ch[1], S - T[T[p].ch[0]].siz - 1, T[p].ch[1], y);
    } else {
        y = p;
        split(T[p].ch[0], S, x, T[p].ch[0]);
    }
    maintain(p);
}
int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y;
    if (T[x].rnd > T[y].rnd) {
        pushdown(x); T[x].ch[1] = merge(T[x].ch[1], y); maintain(x);
        return x;
    } else {
        pushdown(y); T[y].ch[0] = merge(x, T[y].ch[0]); maintain(y);
        return y;
    }
}

void rmv(int x) {
    st[++tot] = x;
    if (T[x].ch[0]) rmv(T[x].ch[0]);
    if (T[x].ch[1]) rmv(T[x].ch[1]);
}
int add(int l, int r) {
    if (l == r) return newNode(a[l]);
    int mid = l + r >> 1;
    return merge(add(l, mid), add(mid + 1, r));
}

int n, m;
int main(void) {
    for (int i = 1; i <= N; ++i) st[++tot] = i;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i);
    root = merge(root, add(1, n));
    char op[15];
    while (m--) {
        scanf("%s", op);
        if (op[0] == 'I') {
            int l, cnt, x, y; scanf("%d%d", &l, &cnt);
            split(root, l, x, y);
            for (int i = 1; i <= cnt; ++i) scanf("%d", a + i);
            root = merge(merge(x, add(1, cnt)), y);
        } else if (op[0] == 'D') {
            int l, cnt, x, y, z; scanf("%d%d", &l, &cnt);
            split(root, l - 1, x, y);
            split(y, cnt, y, z);
            rmv(y); root = merge(x, z);
        } else if (op[4] == '-') {
            int l, cnt, k, x, y, z; scanf("%d%d%d", &l, &cnt, &k);
            split(root, l - 1, x, y);
            split(y, cnt, y, z);
            cover(y, k);
            root = merge(merge(x, y), z);
        } else if (op[0] == 'R') {
            int l, cnt, x, y, z; scanf("%d%d", &l, &cnt);
            split(root, l - 1, x, y);
            split(y, cnt, y, z);
            rever(y);
            root = merge(merge(x, y), z);
        } else if (op[0] == 'G') {
            int l, cnt, x, y, z; scanf("%d%d", &l, &cnt);
            split(root, l - 1, x, y);
            split(y, cnt, y, z);
            printf("%d\n", T[y].sum);
            root = merge(merge(x, y), z);
        } else printf("%d\n", T[root].dat); 
    }
    return 0;
}

Splay

Splay，就是大名鼎鼎的“伸展树（因为伸展是它最经典的操作）”，也叫“自适应查找树”。1985 年由 Daniel Sleator 和 Robert Endre Tarjan（对，就是这个著名的 Tarjan）发明。

Splay 的平衡方式是通过旋转来伸展（有时候叫做“提根”），即把一个叶子节点通过旋转提到根节点。

值得一提的是，Splay 具有“自适应性”，就是它会根据你的操作调整自身结构，使得接下来的查询变得越来越快（像不像并查集）。但即使如此，这货还是很慢。

伸展树有什么用呢？虽然它可以用来实现名次树，但在竞赛中要实现名次树的话，还是乖乖用 Treap 吧。Splay 的伸展操作最大的用处是进行快速地分裂与合并（嗯，就是 fhq-treap 干的事，但实践中还是伸展树用的更多）。

Splay 在旋转时会涉及到节点的爷爷，所以它是双旋平衡树。

伸展操作

Splay 的节点怎么定义呢？一般来说有两种方式。第一种是记录节点的父亲的，因为（哪来那么多因为，这不是上文说的定义吗）。第二种是不记录父亲的。但是第一种相对来讲逻辑更为清晰（尽管旋转操作中的编码较为复杂），第二种在某些情况下会用到。因为笔者是傻瓜，不会第二种，所以这里只介绍第一种情况。

但是这之前，我们还需要搞明白 Splay 最关键的操作：伸展操作（splay 操作）如何进行。

splay 操作要分三种情况考虑。

$x$ 的父节点是根节点，这时候进行一次单旋转即可，就完成了 splay 操作。
$x$ ，它的父节点和它的爷爷“三点共线”，这时进行两次方向相同的旋转操作即可。而且先转 $x$ 的父节点再转 $x$ ；
三点不共线。这是需要将 $x$ 进行不同方向的两次旋转。

通过以上方式我们就能完成 splay 操作啦！

这里可以自行画图感受伸展操作的过程，使得更容易理解接下来的内容。

Splay 实际上有两种写法，第一种方法的节点像这样定义：

struct Node
{
    int ch[2], fa;
    int val;
    // otherthings, such as size and cnt
};

然后我们要实现一些基本的模板，如下：

class Splay
{
    private:
        Node T[100005];
        int tot;
        /*
        inline void maintain(int p)
        { 
            T[p].size = T[T[p].ch[0]].size + T[T[p].ch[1]].size + T[p].cnt;
        }
        */
};

怎么实现旋转呢？由于我们记录了父亲节点，所以可以换一种方式定义旋转：定义 rotate(x) 为将 $x$ 的父亲节点上旋到 $x$ 的爷爷。我们可以写一个函数来判断它是父亲节点的左儿子还是右儿子。

inline int get(int x)
{
    return x == T[T[x].fa].ch[1];
}

旋转操作要注意：因为我们记录了父亲节点，意味着在旋转时需要对每个节点的父亲进行维护。但同时我们也不需要考虑旋转方向了。

inline void rotate(int x)
{
    // y: father, z: grandfather
    int y = T[x].fa, z = T[y].fa, d = get(x); // d 是左右儿子，不是方向
    T[y].ch[d] = T[x].ch[d^1];
    if (T[x].ch[d^1]) T[T[x].ch[d^1]].fa = y;
    T[x].ch[d^1] = y, T[y].fa = x; // 原来的儿子把原来的爸爸当成儿子（上旋）
    // 接下来把本来是爸爸的 y 的爸爸给 x
    T[x].fa = z;
    if (z) T[z].ch[get(y)] = x; // 本来 z 的儿子是 y，现在却变成了 x。如果 z 都等于 0 了还改就没什么意思了，是不？（况且我们还要根据是否等于 0 来判断父亲存不存在）
    maintain(y), maintain(x); // 从下到上重新计算
}

感觉很绕？还是建议自行模拟一下。

有了旋转操作，就不难实现伸展操作了。伸展的原理之前已经讲过，这里直接给出代码：

inline void splay(int x) // 把 x 提根
{
    // 定义 f 为 x 的爸爸
    // 我们需要保证 f 存在（它是 0 就结束了）才能继续循环
    // 常规来讲，我们需要上旋 x
    for (int f = T[x].fa; f = T[x].fa; rotate(x))
        if (T[f].fa) // 如果 T[f].fa 存在，就意味着是情况 2 或 3，需要进行第一次旋转
        {
            rotate(get(x) == get(f) ? f : x); 
            // 当 get(x) == get(f) 时，意为着三点共线，转 f
            // 否则三点不共线，转两次 x（还有一次在循环更新处）
            // 这里的循环顺序很巧妙，保证处理完情况 2 和 3 的特别旋转放送后，立马会进行一次 rotate(x)（for 循环的更新）
        }
    root = x; // 根变成了 x
}

Splay 的第二种写法不记录节点的父亲，这时就变成了递归版的 Splay。~~由于笔者很弱不会~~，所以想学习这种写法请参考《算法竞赛入门经典·训练指南》，或者网上的其它资料。实际上本文介绍的这种写法逻辑更为清晰，这里做无耻推荐（

某些情况下我们会使用指针实现 Splay。实际上笔者更推荐指针，但你的代码必须能跟现有的模块集成。现在大多数选手的 Splay 都是用数组伪指针的形式写的，如果不采用这种形式可能会在今后的学习中造成困扰，所以这里推荐大家使用伪指针。

用 Splay 实现名次树

名次树最终要的就是要保证平衡。但是 Splay 怎么保证平衡？好像很难搞。想想我们 Treap 是怎么搞的吧！用随机来创造平衡。那我们就随机伸展来保证平衡。

~~此处应该有 BGM。~~

不要笑，真是这么搞。听上去比 Treap 更不靠谱？~~我也是这么认为的~~。这里用 Splay 实现名次树仅仅是作为一个练习，考场上用 Treap 就好。

所以结论是：Splay 实现的名次树照样是弱平衡的随机平衡树（而且比 Treap 还慢），不过 Treap 在竞赛中已经足够用了，不建议作死去学 RBT。

注意到一个问题，由于 Splay 是记录父亲的，所以这时候如果我们还使用递归代码就会很麻烦（需要传父亲或者到处都是 get 函数），尤其是插入操作，进行伸展操作前要对性质进行维护，而递归的维护依赖于递归性质，所以这时不如使用迭代。

由于实现删除操作需要运用伸展树的分裂与合并，故这回我们写最初的弱化版。

唯一不同的只有插入操作，剩下的代码都可以照搬。插入要这样进行：动态记录当前节点和当前节点的父亲，如果找到了与要插入的值相同的节点，那么 cnt++，同时伸展这个点；否则递归地往下找，找到了空节点就创建新节点，然后伸展这个点，代码如下：

inline void insert(int val)
{
    int cur = root, fa = 0;
    while (1)
    {
        if (T[cur].val == val) // 找到了值相等的节点
        {
            ++T[cur].cnt;
            maintain(cur);
            maintain(fa);
            // 以上为进行维护
            splay(cur); // 伸展
            return;
        }
        fa = cur;
        cur = T[cur].ch[val > T[cur].val]; // 往下走
        if (cur == 0)
        {
            newNode(val); // 新建节点
            // 重新计算父子关系和子树大小
            T[tot].fa = fa;
            T[fa].ch[val > T[fa].val] = tot;
            maintain(fa);
            splay(tot); // 伸展
            return;
        }
    }
}

查看代码

#include <iostream>
#include <cstdio>

using namespace std;

const int INF = 0x7fffffff;

struct Node 
{
    int ch[2], fa;
    int val;
    int size, cnt;
};

class Splay
{
    public:
        int root;
    private:
        Node T[100005];
        int tot;
        inline void newNode(int val)
        {
            T[++tot].val = val;
            T[tot].size = T[tot].cnt = 1;
        }
        inline void maintain(int p)
        {
            T[p].size = T[T[p].ch[0]].size + T[T[p].ch[1]].size + T[p].cnt;
        }
        inline int get(int x)
        {
            return x == T[T[x].fa].ch[1];
        }
        inline void rotate(int x)
        {
            int y = T[x].fa, z = T[y].fa, d = get(x);
            T[y].ch[d] = T[x].ch[d^1];
            if (T[x].ch[d^1]) T[T[x].ch[d^1]].fa = y;
            T[x].ch[d^1] = y, T[y].fa = x;
            T[x].fa = z;
            if (z) T[z].ch[y == T[z].ch[1]] = x;
            maintain(y);
            maintain(x);
        }
        inline void splay(int x)
        {
            for (int f = T[x].fa; f = T[x].fa; rotate(x))
                if (T[f].fa) rotate(get(x) == get(f) ? f : x);
            root = x;
        }
    public:
        inline void build(void)
        {
            newNode(-INF), newNode(INF);
            T[1].ch[1] = 2, T[2].fa = 1;
            maintain(root = 1);
        }
        inline void insert(int val)
        {
            int cur = root, fa = 0;
            while (1)
            {
                if (T[cur].val == val)
                {
                    ++T[cur].cnt;
                    maintain(cur);
                    maintain(fa);
                    splay(cur);
                    return;
                }
                fa = cur;
                cur = T[cur].ch[val > T[cur].val];
                if (cur == 0)
                {
                    newNode(val);
                    T[tot].fa = fa;
                    T[fa].ch[val > T[fa].val] = tot;
                    maintain(fa);
                    splay(tot);
                    return;
                }
            }
        }
        int Rank(int p, int val)
        {
            if (p == 0) return 1;
            if (val == T[p].val) return T[T[p].ch[0]].size + 1;
            if (val < T[p].val) return Rank(T[p].ch[0], val);
            return Rank(T[p].ch[1], val) + T[T[p].ch[0]].size + T[p].cnt;
        }
        int kth(int p, int rnk)
        {
            if (p == 0) return INF;
            if (rnk <= T[T[p].ch[0]].size) return kth(T[p].ch[0], rnk);
            if (rnk <= T[T[p].ch[0]].size + T[p].cnt) return T[p].val;
            return kth(T[p].ch[1], rnk - T[T[p].ch[0]].size - T[p].cnt);
        }
        inline int GetPre(int val)
        {
            int ans = 1, p = root;
            while (p)
            {
                if (val == T[p].val)
                {
                    if (T[p].ch[0])
                    {
                        p = T[p].ch[0];
                        while (T[p].ch[1]) p = T[p].ch[1];
                        ans = p;
                    }
                    break;
                }
                if (T[p].val < val && T[p].val > T[ans].val) ans = p;
                p = T[p].ch[val < T[p].val ? 0 : 1];
            }
            return T[ans].val;
        }
        inline int GetNext(int val)
        {
            int ans = 2, p = root;
            while (p)
            {
                if (val == T[p].val)
                {
                    if (T[p].ch[1])
                    {
                        p = T[p].ch[1];
                        while (T[p].ch[0]) p = T[p].ch[0];
                        ans = p;
                    }
                    break;
                }
                if (T[p].val > val && T[p].val < T[ans].val) ans = p;
                p = T[p].ch[val < T[p].val ? 0 : 1];
            }
            return T[ans].val;
        }
}T;

inline int read(void)
{
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int main(void)
{
    int q = read();
    T.build();
    while (q--)
    {
        int op = read(), x = read();
        if (op == 1) printf("%d\n", T.Rank(T.root, x) - 1);
        else if (op == 2) printf("%d\n", T.kth(T.root, x + 1));
        else if (op == 3) printf("%d\n", T.GetPre(x));
        else if (op == 4) printf("%d\n", T.GetNext(x));
        else T.insert(x);
    }
    return 0;
}

分裂与合并

由于 Splay 支持伸展操作，因此它可以很方便的进行分裂与合并，进而实现可以分裂与合并的序列。模板。

神风敢死队炸毁了此处的内容。

鉴定为不如 FHQ，以后再说。

Problemset

直接的平衡树应用很少，但是也有。

可分裂与合并的序列

用于维护序列，但可能需要一些思考。

[JSOI2008] 火星人

Portal.

LCQ 的查询直接二分即可，剩下就是直接平衡树。

查看代码

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long u64;
const int B = 10009, N = 100000;

int n, m;
u64 h[100005];
char s[100005];
mt19937 Rand(time(0));

struct Node {
    int ch[2], siz, rnd;
    u64 w; char c;
} T[100005];
int tot, root;
int newNode(char c) {
    T[++tot].rnd = Rand(); T[tot].siz = 1; T[tot].w = T[tot].c = c;
    return tot;
}
void maintain(int p) {
    T[p].siz = T[T[p].ch[0]].siz + T[T[p].ch[1]].siz + 1;
    T[p].w = T[T[p].ch[0]].w * h[T[T[p].ch[1]].siz + 1] + T[p].c * h[T[T[p].ch[1]].siz] + T[T[p].ch[1]].w;
}
void split(int p, int S, int &x, int &y) {
    if (!p) return x = y = 0, void();
    if (T[T[p].ch[0]].siz + 1 <= S) {
        x = p;
        split(T[p].ch[1], S - T[T[p].ch[0]].siz - 1, T[p].ch[1], y);
    } else {
        y = p;
        split(T[p].ch[0], S, x, T[p].ch[0]);
    }
    maintain(p);
}
int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y;
    if (T[x].rnd > T[y].rnd) {
        T[x].ch[1] = merge(T[x].ch[1], y); maintain(x);
        return x;
    } else {
        T[y].ch[0] = merge(x, T[y].ch[0]); maintain(y);
        return y;
    }
}
int add(int l, int r) {
    if (l == r) return newNode(s[l]);
    int mid = l + r >> 1;
    return merge(add(l, mid), add(mid + 1, r));
}
u64 Get(int l, int len) {
    int x, y, z;
    split(root, l - 1, x, y);
    split(y, len, y, z);
    u64 res = T[y].w; 
    root = merge(merge(x, y), z);
    return res;
}

int main(void) {
    for (int i = h[0] = 1; i <= N; ++i) h[i] = h[i - 1] * B;
    scanf("%s", s + 1); n = strlen(s + 1); root = merge(root, add(1, n));
    scanf("%d", &m);
    char op[5]; int p, q, x, y, z;
    while (m--) {
        scanf("%s%d", op, &p);
        if (op[0] == 'Q') {
            scanf("%d", &q);
            int L = 0, R = T[root].siz - q + 2;
            while (L + 1 != R) {
                int mid = L + R >> 1;
                if (Get(p, mid) == Get(q, mid)) L = mid;
                else R = mid;
            }
            printf("%d\n", L);
        } else if (op[0] == 'R') {
            scanf("%s", s);
            split(root, p - 1, x, y);
            split(y, 1, y, z);
            T[y].w = T[y].c = s[0];
            root = merge(merge(x, y), z);
        } else {
            scanf("%s", s);
            split(root, p, x, y);
            root = merge(merge(x, newNode(s[0])), y);
        }
    }
    return 0;
}

[HNOI2011] 括号修复

Portal.

修复一个括号序列的代价这样计算：设 ( = -1, ) = 1，前缀最大值为 $a$ ，后缀最小值为 $b$ ，代价是 $\lceil a\div 2\rceil+\lceil -b\div 2\rceil$ 。然后直接使用平衡树维护即可。

查看代码

#include <iostream>
#include <cstdio>
#include <random>

using namespace std;

mt19937 Rand(time(0));
struct Node {
    int ch[2], siz, rnd;
    int setv; bool rev, inv;
    int lmax, lmin, rmax, rmin, sum, val;
} T[100005];
int root, tot, n, m;
int newNode(int val) {
    T[++tot].rnd = Rand(); T[tot].siz = 1; 
    T[tot].sum = T[tot].val = val;
    if (val == 1) T[tot].lmax = T[tot].rmax = 1;
    else T[tot].lmin = T[tot].rmin = -1;
    return tot;
}
void maintain(int p) {
    int l = T[p].ch[0], r = T[p].ch[1];
    T[p].siz = T[l].siz + T[r].siz + 1;
    T[p].sum = T[l].sum + T[r].sum + T[p].val;
    T[p].lmax = max(T[l].lmax, T[l].sum + T[p].val + T[r].lmax);
    T[p].lmin = min(T[l].lmin, T[l].sum + T[p].val + T[r].lmin);
    T[p].rmax = max(T[r].rmax, T[r].sum + T[p].val + T[l].rmax);
    T[p].rmin = min(T[r].rmin, T[r].sum + T[p].val + T[l].rmin);
}
void Replace(int p, int val) {
    T[p].val = T[p].setv = val; T[p].sum = val * T[p].siz;
    T[p].lmax = T[p].rmax = max(0, val * T[p].siz);
    T[p].lmin = T[p].rmin = min(0, val * T[p].siz);
}
void Swap(int p) {
    swap(T[p].ch[0], T[p].ch[1]); 
    swap(T[p].lmax, T[p].rmax); swap(T[p].lmin, T[p].rmin);
    T[p].rev ^= 1;
}
void Invert(int p) {
    T[p].val = -T[p].val; T[p].sum = -T[p].sum; T[p].setv = -T[p].setv;
    int x = T[p].lmax, y = T[p].lmin; T[p].lmax = -y, T[p].lmin = -x;
    x = T[p].rmax, y = T[p].rmin; T[p].rmax = -y, T[p].rmin = -x;
    T[p].inv ^= 1;
}
void pushdown(int p) {
    int l = T[p].ch[0], r = T[p].ch[1];
    if (T[p].inv) {
        if (l) Invert(l); if (r) Invert(r);
        T[p].inv = 0;
    }
    if (T[p].rev) {
        if (l) Swap(l); if (r) Swap(r);
        T[p].rev = 0;
    }
    if (T[p].setv) {
        if (l) Replace(l, T[p].setv); if (r) Replace(r, T[p].setv);
        T[p].setv = 0;
    }
}
void split(int p, int S, int &x, int &y) {
    if (!p) return x = y = 0, void(); pushdown(p);
    if (T[T[p].ch[0]].siz + 1 <= S) {
        x = p;
        split(T[p].ch[1], S - T[T[p].ch[0]].siz - 1, T[p].ch[1], y);
    } else {
        y = p;
        split(T[p].ch[0], S, x, T[p].ch[0]);
    }
    maintain(p);
}
int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y;
    if (T[x].rnd > T[y].rnd) {
        pushdown(x); T[x].ch[1] = merge(T[x].ch[1], y); maintain(x);
        return x;
    } else {
        pushdown(y); T[y].ch[0] = merge(x, T[y].ch[0]); maintain(y);
        return y;
    }
}

char s[100005];
int add(int l, int r) {
    if (l == r) return newNode(s[l] == '(' ? -1 : 1);
    int mid = l + r >> 1;
    return merge(add(l, mid), add(mid + 1, r));
}

int main(void) {
    scanf("%d%d%s", &n, &m, s + 1); root = add(1, n);
    char op[15]; int l, r, x, y, z;
    while (m--) {
        scanf("%s%d%d", op, &l, &r);
        if (op[0] == 'R') {
            scanf("%s", s);
            split(root, l - 1, x, y);
            split(y, r - l + 1, y, z);
            Replace(y, s[0] == '(' ? -1 : 1);
            root = merge(merge(x, y), z);
        } else if (op[0] == 'S') {
            split(root, l - 1, x, y);
            split(y, r - l + 1, y, z);
            Swap(y);
            root = merge(merge(x, y), z);
        } else if (op[0] == 'I') {
            split(root, l - 1, x, y);
            split(y, r - l + 1, y, z);
            Invert(y);
            root = merge(merge(x, y), z);
        } else {
            split(root, l - 1, x, y);
            split(y, r - l + 1, y, z);
            printf("%d\n", (T[y].lmax + 1) / 2 + (1 - T[y].rmin) / 2);
            root = merge(merge(x, y), z);
        }
    }
    return 0;
}

[ZJOI2006] 书架

Portal.

问题在于如何高效找到一个节点在平衡树上的位置（中序遍历的编号）。维护每一个节点的父亲，然后直接从这个节点的位置跳到根，维护中序遍历的位置。这之后直接乱做即可。

查看代码

#include <bits/stdc++.h>
using namespace std;

int n, m; 
struct Node {
    int ch[2], fa, siz, dat, val; 
} T[200005];
int tot = 0, root, id[200005]; // 编号为 i 的节点是平衡树中的 id[i] 号节点 
mt19937 Rand(time(0));
void maintain(int p) { T[p].siz = T[T[p].ch[0]].siz + T[T[p].ch[1]].siz + 1; }
int newNode(int val) {
    T[++tot].val = val; T[tot].dat = Rand(); T[tot].siz = 1;
    return id[val] = tot; 
}
void split(int p, int S, int &x, int &y, int fax = 0, int fay = 0) {
    if (!p) return x = y = 0, void(); 
    if (T[T[p].ch[0]].siz + 1 <= S) {
        x = p; T[x].fa = fay; 
        split(T[p].ch[1], S - T[T[p].ch[0]].siz - 1, T[p].ch[1], y, fax, x);
    } else {
        y = p; T[y].fa = fax; 
        split(T[p].ch[0], S, x, T[p].ch[0], y, fay); 
    } maintain(p);
}
int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y;
    if (T[x].dat > T[y].dat) {
        T[x].ch[1] = merge(T[x].ch[1], y); maintain(x);
        T[T[x].ch[1]].fa = x; return x;
    } else {
        T[y].ch[0] = merge(x, T[y].ch[0]); maintain(y);
        T[T[y].ch[0]].fa = y; return y;
    }
}
int find(int ID) { // 中序遍历的编号 
	int res = T[T[ID].ch[0]].siz + 1; 
	while (ID != root && ID) {
		if (T[T[ID].fa].ch[1] == ID) res += T[T[T[ID].fa].ch[0]].siz + 1; 
		ID = T[ID].fa; 
	}
	return res; 
}

int main(void) {
    scanf("%d%d", &n, &m);
    while (n--) {
    	int x; scanf("%d", &x); 
    	root = merge(root, newNode(x)); 
	}
	char op[10]; int s, t; 
	while (m--) {
		scanf("%s%d", op, &s); 
		if (op[0] == 'T') {
			int x, y, z; s = find(id[s]); 
			split(root, s - 1, x, y); split(y, 1, y, z); 
			root = merge(y, merge(x, z)); 
		} else if (op[0] == 'B') {
			int x, y, z; s = find(id[s]); 
			split(root, s - 1, x, y); split(y, 1, y, z); 
			root = merge(x, merge(z, y)); 
		} else if (op[0] == 'I') {
			scanf("%d", &t); s = find(id[s]); 
			int r1, r2, r3, r4; 
			if (t == 1) {
				split(root, s - 1, r1, r2); split(r2, 1, r2, r3); split(r3, 1, r3, r4); 
				root = merge(r1, merge(r3, merge(r2, r4))); 
			} else if (t == -1) {
				split(root, s - 2, r1, r2); split(r2, 1, r2, r3); split(r3, 1, r3, r4);  
				root = merge(r1, merge(r3, merge(r2, r4))); 
			}
		} else if (op[0] == 'A') printf("%d\n", find(id[s]) - 1); 
		else {
			int x, y; split(root, s, x, y); 
			int node = x; 
			while (T[node].ch[1]) node = T[node].ch[1]; 
			printf("%d\n", T[node].val); 
			root = merge(x, y); 
		}
	}
    return 0;
}

综合应用

一些平衡树的简单应用。

[POI2015] LOG

Portal.

使用一棵维护权值的平衡树。在减 $1$ 的过程中，大于等于 $s$ 的是随便用，剩下的只需要考虑它们的和是否够用即可（可以将后面的向前移来叠到 $s$ ，这样保证一层中不会有来自同一个位置的数）。

查看代码

#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 

mt19937 Rand(time(0)); 
struct Node {
    int ls, rs, siz, rnd; 
    i64 sum, val; 
} T[2000005];
int root, tot; 
int newNode(int x) {
    ++tot; T[tot].rnd = Rand(); T[tot].siz = 1; 
    T[tot].sum = T[tot].val = x; 
    return tot; 
}
inline void maintain(int p) {
    T[p].siz = T[T[p].ls].siz + T[T[p].rs].siz + 1; 
    T[p].sum = T[T[p].ls].sum + T[T[p].rs].sum + T[p].val; 
}
void split(int p, int k, int &x, int &y) {
    if (!p) return x = y = 0, void(); 
    if (T[p].val <= k) {
        x = p; 
        split(T[p].rs, k, T[p].rs, y);
    } else {
        y = p; 
        split(T[p].ls, k, x, T[p].ls);
    }
    maintain(p); 
}
int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y; 
    if (T[x].rnd > T[y].rnd) {
        T[x].rs = merge(T[x].rs, y); maintain(x); 
        return x; 
    } else {
        T[y].ls = merge(x, T[y].ls); maintain(y); 
        return y; 
    }
}
void insert(int v) {
    int x, y; split(root, v, x, y);
    root = merge(x, merge(newNode(v), y)); 
}
void remove(int v) {
    int x, y, z; split(root, v, x, z); split(x, v - 1, x, y);
    if (y) y = merge(T[y].ls, T[y].rs); 
    root = merge(x, merge(y, z));
}
int bigger(int s) {
    int x, y; split(root, s - 1, x, y);
    int ans = T[y].siz; root = merge(x, y); 
    return ans; 
}
i64 query(int v) {
    int x, y; split(root, v - 1, x, y);
    i64 ans = T[x].sum; root = merge(x, y); 
    return ans; 
}

int n, m, a[1000005]; 

int main(void) {
    scanf("%d%d", &n, &m); char op[5]; int x, y; 
    for (int i = 1; i <= n; ++i) insert(0); 
    while (m--) {
        scanf("%s%d%d", op, &x, &y); 
        if (op[0] == 'U') remove(a[x]), insert(a[x] = y); 
        else {
            int num = bigger(y); 
            if (query(y) >= 1ll * (x - num) * y) puts("TAK"); 
            else puts("NIE"); 
        }
    }
    return 0;
}

[HNOI2012] 永无乡

Portal.

用 Treap 维护名次，然后启发式合并。

查看代码

#include <bits/stdc++.h>
using namespace std;

struct Node {
    int ch[2];
    int val, dat;
    int siz;
} T[3000005]; 
int tot, root[100005], f[100005], idx[100005];
int find(int x) { if (f[x] == x) return x; return find(f[x]); }

void maintain(int p) { T[p].siz = T[T[p].ch[0]].siz + T[T[p].ch[1]].siz + 1; }
inline int newNode(int val) {
    T[++tot].val = val; T[tot].dat = rand();
    T[tot].siz = 1; T[tot].ch[0] = T[tot].ch[1] = 0;
    return tot;
}
inline void rotate(int& p, int d) {
    int q = T[p].ch[d ^ 1];
    T[p].ch[d ^ 1] = T[q].ch[d], T[q].ch[d] = p, p = q;
    maintain(T[p].ch[d]), maintain(p);
}
void insert(int& p, int val) {
    if (p == 0) return p = newNode(val), void(); 
    else {
        int d = (val < T[p].val ? 0 : 1);
        insert(T[p].ch[d], val);
        if (T[T[p].ch[d]].dat > T[p].dat) rotate(p, d ^ 1);
    }
    maintain(p);
}
int kth(int p, int rnk) {
    if (p == 0) return 0;
    if (rnk <= T[T[p].ch[0]].siz) return kth(T[p].ch[0], rnk);
    if (rnk <= T[T[p].ch[0]].siz + 1) return T[p].val;
    return kth(T[p].ch[1], rnk - T[T[p].ch[0]].siz - 1);
}
void dfs(int x, int y) {
    insert(root[y], T[x].val);
    if (T[x].ch[0]) dfs(T[x].ch[0], y);
    if (T[x].ch[1]) dfs(T[x].ch[1], y);
}
inline void merge(int u, int v) {
    u = find(u); v = find(v); 
    if (u == v) return; 
    if (T[root[u]].siz > T[root[v]].siz) swap(u, v);
    f[u] = v; dfs(root[u], v);
}

int n, m, q; 
int a[100005]; 

int main(void) {
    scanf("%d%d", &n, &m, &q);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i), root[i] = newNode(a[i]), f[i] = idx[a[i]] = i;
    while (m--) {
        int u, v; scanf("%d%d", &u, &v);
        merge(u, v);
    }
    char op[5]; int x, y; 
    for (scanf("%d", &q); q--; ) {
        scanf("%s%d%d", op, &x, &y);
        if (op[0] == 'Q') {
            x = find(x);
            int k = kth(root[x], y);
            if (!k) puts("-1");
            else printf("%d\n", idx[k]);
        }
        else merge(x, y); 
    }
    return 0;
}

[Luogu P3987] 我永远喜欢珂朵莉~

Portal.

一个数最多被除 $\log$ 次，那么可以暴力修改并使用 Fenwick 树查询，使用平衡树维护有因数 $x$ 的数，每次修改时直接 DFS 分裂出的子树。时间复杂度 $O(nd(V)+n\log n\log v+m\log n)$ 。

查看代码

#include <bits/stdc++.h>
#define lowbit(x) (x & -x)
using namespace std;
typedef long long i64; 

int n, m, a[100005]; 
vector<int> g[500005]; 

i64 C[100005];
void add(int x, int k) {
    for (; x <= n; x += lowbit(x)) C[x] += k;
}
i64 query(int x) {
    i64 res = 0; 
    for (; x; x -= lowbit(x)) res += C[x];
    return res;
}

mt19937 Rand(time(0)); 
struct Node {
    int ls, rs, rnd, v, siz; 
} T[65000005];
int tot, root[500005];
void maintain(int o) { T[o].siz = T[T[o].ls].siz + T[T[o].rs].siz + 1; }
int newNode(int v) {
    ++tot; T[tot].ls = T[tot].rs = 0; 
    T[tot].v = v; T[tot].siz = 1; T[tot].rnd = Rand();
    return tot; 
}
int merge(int x, int y) {
    if (x == 0 || y == 0) return x + y; 
    if (T[x].rnd > T[y].rnd) return T[x].rs = merge(T[x].rs, y), maintain(x), x;
    return T[y].ls = merge(x, T[y].ls), maintain(y), y;  
}
void split(int p, int k, int &x, int &y) {
    if (!p) return x = y = 0, void();
    if (T[p].v <= k) x = p, split(T[p].rs, k, T[p].rs, y);
    else y = p, split(T[p].ls, k, x, T[p].ls);
    maintain(p);
}
int cur, q[100005];
int build(int l, int r) {
    if (l > r) return 0;
    if (l == r) return newNode(q[l]);
    int mid = l + r >> 1; 
    return merge(build(l, mid), build(mid + 1, r));
}
void dfs(int x, int v) {
    if (!x) return;
    if (T[x].ls) dfs(T[x].ls, v); int p = T[x].v; 
    if (a[p] % v == 0) {
        add(p, -a[p]), a[p] /= v, add(p, a[p]); 
        if (a[p] % v == 0) q[++cur] = p;
    }
    if (T[x].rs) dfs(T[x].rs, v);
}
void update(int x, int l, int r) {
    int a, b, c; split(root[x], r, b, c); split(b, l - 1, a, b);
    cur = 0; dfs(b, x); root[x] = merge(a, merge(build(1, cur), c));
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", a + i); add(i, a[i]);
        for (int j = 1; j * j <= a[i]; ++j) if (a[i] % j == 0) {
            g[j].emplace_back(i);
            if (j * j != a[i]) g[a[i] / j].emplace_back(i);
        }
    }
    for (int i = 1; i <= 500000; ++i) {
        cur = 0; 
        for (int x : g[i]) q[++cur] = x; 
        root[i] = build(1, cur);
    }
    while (m--) {
        int op, l, r, x; scanf("%d%d%d", &op, &l, &r);
        if (op == 1) {
            scanf("%d", &x);
            if (x > 1) update(x, l, r);
        } else printf("%lld\n", query(r) - query(l - 1));
    }
    return 0;
}

对于数据加强版 [Ynoi2013] 大学，平衡树常数过大，不能通过。对于每一个约数采用一个并查集，开始时每个数都指向自己，删除时将当前数的父亲设置为下一个数。另外 STL vector 的常数过大，需要手写内存池。

查看代码

#include <bits/stdc++.h>
#define lowbit(x) (x & -x)
#define i64 long long
using namespace std;

int n, m, a[100005], o[500005], pool[40000005]; 
int *g[500005], *poi = pool, *fa[500005]; 
int find(int k, int x) {
    if (x == o[k] || fa[k][x] == x) return x;
    return fa[k][x] = find(k, fa[k][x]); 
}

i64 C[100005];
inline void add(int x, int k) {
    for (; x <= n; x += lowbit(x)) C[x] += k;
}
inline i64 query(int x) {
    i64 res = 0; 
    for (; x; x -= lowbit(x)) res += C[x];
    return res;
}

int main(void) {
    scanf("%d%d", &n, &m); int maxx = 0, op, l, r, x; i64 last = 0; 
    for (int i = 1; i <= n; ++i) {
        scanf("%d", a + i); add(i, a[i]); maxx = max(maxx, a[i]);
        ++o[a[i]];
    }
    for (int i = 1; i <= maxx; ++i) for (int j = i + i; j <= maxx; j += i) o[i] += o[j];
    for (int i = 1; i <= maxx; ++i) {
        g[i] = poi; poi += o[i]; fa[i] = poi; poi += o[i];
        for (int j = 0; j < o[i]; ++j) fa[i][j] = j; 
        o[i] = 0; 
    }
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j * j <= a[i]; ++j) if (a[i] % j == 0) {
            g[j][o[j]++] = i; 
            if (j * j != a[i]) g[a[i] / j][o[a[i] / j]++] = i; 
        }
    while (m--) {
        scanf("%d%d%d", &op, &l, &r); l ^= last, r ^= last; 
        if (op == 1) {
            scanf("%d", &x); x ^= last; 
            if (x == 1 || !o[x]) continue; 
            for (int i = find(x, lower_bound(g[x], g[x] + o[x], l) - g[x]); i < o[x] && g[x][i] <= r; i = find(x, i + 1)) {
                if (a[g[x][i]] % x == 0) add(g[x][i], a[g[x][i]] / x - a[g[x][i]]), a[g[x][i]] /= x;
                if (a[g[x][i]] % x) fa[x][i] = i + 1; 
            }
        } else printf("%lld\n", last = query(r) - query(l - 1));
    }
    return 0;
}

[Ynoi2010] y-fast trie

Portal.

神仙题。

加入集合时将 $x$ 取模，然后对于两个答案数 $i,j$ 分类讨论：

$C\ge i+j<2C$ ，这样只需要维护集合的最大和次大值即可。
$0\le i+j<C$ ，我们讨论这种情况。

称一个数 $i$ 在集合中满足 $i+j<C$ 的最大数 $j$ 是 $i$ 的最优匹配，我们需要实现一个可以求出 $i$ 的匹配的函数，并且能够向它指定是否不能匹配到自身。

一个数的改变可能会影响 $O(n)$ 个匹配。根据经验，我们需要删去一些无用的匹配，让需要修改的匹配个数控制在 $O(1)$ 级别。比如 $x$ 的最优匹配是 $y$ ，而 $y$ 的最优匹配是 $z$ ，有 $x\le z$ ，那么 $x$ 加入时就不需要修改 $y$ 的最优匹配，因为现有的答案 $y+z$ 一定比 $x+y$ 大，进而 $y,z$ 必须双向互为最优匹配这个答案才需要被删除，但是 $x+y$ 一定要被插入。

删除 $x$ 时， $x+y$ 一定要被删除，如果 $y,z$ 互为最优匹配需要将 $y+z$ 插入回来。

查看代码

#include <bits/stdc++.h>
using namespace std;

int n, C, siz; 
multiset<int> a, b; 

int find(int x, int op) { // 寻找 i + j < C 的最大 j, op = 1 为强制不等于自己
    if (x == -1) return -1; 
    auto it = a.upper_bound(C - 1 - x); 
    if (it == a.begin()) return -1; --it; // 满足 x + j < C 的最大 j
    if (op && *it == x && a.count(x) == 1) return it == a.begin() ? -1 : *--it; 
    return *it; 
}
inline void insert(int x) { 
    if (++siz == 1) return a.insert(x), void(); 
    int y = find(x, 0), z = find(y, 1), w = find(z, 1); // 看 x 的最优匹配 y，x 是否能对 y 本身的最优匹配 z 产生影响，而且 y,z 双向匹配
    // 寻找 x 的匹配可以是 x，因为 x 还没进集合
    if (y != -1 && z < x) {
        if (z != -1 && w == y) b.erase(b.find(y + z)); 
        b.insert(x + y);
    }
    a.insert(x); 
}
inline void remove(int x) {
    a.erase(a.find(x)); 
    if (--siz == 0) return; 
    int y = find(x, 0), z = find(y, 1), w = find(z, 1); // 删除了 x，将 x 的最优匹配 y 的最优匹配进行修改
    if (y != -1 && z < x) {
        if (z != -1 && w == y) b.insert(y + z); 
        b.erase(b.find(x + y)); 
    }
}
inline int query(int x) { // i + j >= C
    auto it = --a.end(); 
    if (a.count(*it) >= 2) return *it * 2 % C; 
    int tmp = *it; --it; return (tmp + *it) % C; 
}

int main(void) {
    scanf("%d%d", &n, &C); int last = 0; 
    while (n--) {
        int op, x; scanf("%d%d", &op, &x); x = (x ^ last) % C; 
        if (op == 1) insert(x); else remove(x); 
        if (siz < 2) puts("EE"), last = 0; 
        else printf("%d\n", last = max(query(x), b.empty() ? 0 : *--b.end()));
    }
    return 0;
}

* [Ynoi2015] 人人本着正义之名

Portal.

首先看一看操作 $3\sim 6$ 是个什么东西。

将 $[l,r-1]$ 中的数 $a_i$ 同时变为 $a_i$ 与 $a_{i+1}$ 按位或的值？简单，就是所有极长 $0$ 段最右边一个 $0$ 变成 $1$ 。

搞一个平衡树，打一个标记表示左右端点的移动量。只有两个问题：

如何保证区间极长？区间染色时向左右拓展一下即可。
如何保证没有空区间？区间数量是 $O(n+m)$ 的，维护最短 01 区间长度，暴力找，然后将其左右区间合并即可。

本质上不难，但代码比较壮观，需要使用指针实现平衡树进行卡常。

查看代码

#include <bits/stdc++.h>
#define PTREE(x) printf("root = %d\n", x); printT(x)
#define DEBUG fprintf(stderr, "Passed Line %d, in Function %s\n", __LINE__, __FUNCTION__)
using namespace std; 
const int INF = 1e9; 

mt19937 Rand(time(0)); 
inline int read(void) {
    int x = 0, c = getchar(); 
    while (!isdigit(c)) c = getchar(); 
    while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); 
    return x; 
}
void print(int x) {
    if (x > 9) print(x / 10); 
    putchar(x % 10 ^ 48); 
}

struct Node {
    int rnd; 
    int col, sum, siz[2]; // 区间颜色，区间和，01 区间数量
    int l, r; // 左右端点
    int dL, dR; // 1 的左右端点位移
    int minLen[2]; // 最短 01 区间长度
    Node *ls, *rs; 
    void reset(void) {
        siz[col] = 1; siz[!col] = 0; sum = col * (r - l + 1); dL = dR = 0; 
        minLen[col] = r - l + 1; minLen[!col] = INF; 
    }
    Node(int col = 0, int l = 0, int r = 0) : rnd(Rand()), col(col), l(l), r(r), ls(NULL), rs(NULL) { reset(); }
    void add(const Node &a) {
        sum += a.sum; siz[0] += a.siz[0]; siz[1] += a.siz[1]; 
        minLen[0] = min(minLen[0], a.minLen[0]); 
        minLen[1] = min(minLen[1], a.minLen[1]); 
    }
} T[5000005];   
Node* root; int tot; 
inline Node* newNode(int col, int l, int r) { return &(T[++tot] = Node(col, l, r)); }
inline void maketag(Node* o, int dL, int dR) {
    o->dL += dL; o->dR += dR; 
    o->minLen[0] -= dL + dR; o->minLen[1] += dL + dR; 
    o->sum += (dL + dR) * o->siz[1]; 
    if (o->col == 1) o->l -= dL, o->r += dR; 
    else o->l += dR, o->r -= dL; 
}
inline void pushdown(Node* o) {
    if (!o->dL && !o->dR) return; 
    if (o->ls != NULL) maketag(o->ls, o->dL, o->dR); 
    if (o->rs != NULL) maketag(o->rs, o->dL, o->dR); 
    o->dL = o->dR = 0; 
}
inline void pushup(Node* o) {
    o->reset(); 
    if (o->ls) o->add(*(o->ls)); 
    if (o->rs) o->add(*(o->rs)); 
}
Node* merge(Node* x, Node* y) {
    if (x == NULL) return y; if (y == NULL) return x; 
    if (x->rnd < y->rnd) {
        pushdown(x); x->rs = merge(x->rs, y); 
        pushup(x); return x; 
    } else {
        pushdown(y); y->ls = merge(x, y->ls); 
        pushup(y); return y; 
    }
}
// 左端点 <= k 划到 x
void split1(Node* o, int k, Node*& x, Node*& y) {
    if (o == NULL) return x = y = NULL, void(); pushdown(o); 
    if (o->l <= k) x = o, split1(x->rs, k, x->rs, y); 
    else y = o, split1(y->ls, k, x, y->ls); 
    pushup(o); 
}
// 右端点 <= k 划到 x
void split2(Node* o, int k, Node*& x, Node*& y) {
    if (o == NULL) return x = y = NULL, void(); pushdown(o); 
    if (o->r <= k) x = o, split2(x->rs, k, x->rs, y); 
    else y = o, split2(y->ls, k, x, y->ls); 
    pushup(o); 
}

// 删除空区间
Node* Eraser[3000005]; int L = 1, R = 0; 
const int B = 4194303; 
void findEmpty(Node* o) {
    if (o == NULL) return; 
    if (o->minLen[0] && o->minLen[1]) return; 
    pushdown(o); 
    if (o->l > o->r) Eraser[(++R) & B] = o; 
    findEmpty(o->ls); findEmpty(o->rs); 
}
inline void Erase(void) {
    while (L <= R) {
        Node *o = Eraser[(L++) & B]; 
        Node *nodeL, *TM, *nodeR, *TR; 
        split1(root, o->l - 1, root, TM); split1(TM, o->l, TM, TR); // TM.l = o->l
        split2(root, o->l - 2, root, nodeL); 
        nodeR = (o == TM ? o->rs : TM); 
        if (nodeL && nodeR) nodeL->r = nodeR->r, nodeL->reset(), nodeR = NULL; 
        root = merge(root, merge(nodeL, merge(nodeR, TR))); 
    }
}

void printT(Node* o) {
    if (o == NULL) return; pushdown(o); 
    if (o->ls) printT(o->ls); 
    printf("%d %d %d %d %d\n", o->l, o->r, o->dL, o->dR, o->col); 
    if (o->rs) printT(o->rs); 
}

// 操作列表
inline void cover(int l, int r, int col) {
    Node *nodeL, *TM, *nodeR, *TR; // root = TL
    split2(root, l - 1, root, TM); split1(TM, r, TM, TR); 
    split1(TM, l - 1, nodeL, TM); split2(TM, r, TM, nodeR); 
    if (nodeL) {
        if (nodeL->r > r) nodeR = newNode(nodeL->col, r, nodeL->r); 
        nodeL->r = l - 1; nodeL->reset(); 
    } else split2(root, l - 2, root, nodeL); 
    if (nodeR) nodeR->l = r + 1, nodeR->reset(); 
    else split1(TR, r + 1 , nodeR, TR); 
    TM = newNode(col, l, r); 
    if (nodeL && TM->col == nodeL->col) TM->l = nodeL->l, TM->reset(), nodeL = NULL;
    if (nodeR && TM->col == nodeR->col) TM->r = nodeR->r, TM->reset(), nodeR = NULL; 
    root = merge(root, merge(nodeL, merge(TM, merge(nodeR, TR)))); 
}
// 0 区间右端点 -1，1 区间左端点 -1
inline void opt3(int l, int r) {
    --r; Node *TM, *TR, *node; 
    split2(root, l - 1, root, TM); split1(TM, r, TM, TR); 
    split1(TM, l, node, TM); 
    if (node && node->col == 1) root = merge(root, node); 
    else TM = merge(node, TM); 
    split2(TM, r - 1, TM, node); 
    if (node && node->col == 0) {
        if (node->r > r) TR = merge(node, TR); 
        else {
            TM = merge(TM, node); 
            split1(TR, r + 1, node, TR); 
            TM = merge(TM, node); 
        }
    } else TM = merge(TM, node); 
    // PTREE(TM); 
    if (TM) maketag(TM, 1, 0); 
    // PTREE(TM); 
    root = merge(merge(root, TM), TR); 
    findEmpty(root); Erase(); 
}
// 0 区间左端点 +1，1 区间右端点 +1
inline void opt4(int l, int r) {
    ++l; Node *TM, *TR, *node; 
    split2(root, l - 1, root, TM); split1(TM, r, TM, TR); 
    split1(TM, l, node, TM); 
    if (node && node->col == 0) {
        if (node->l < l) root = merge(root, node); 
        else {
            TM = merge(node, TM); 
            split2(root, l - 2, root, node); 
            TM = merge(node, TM); 
        }
    } else TM = merge(node,TM); 
    split2(TM, r - 1, TM, node); 
    if (node && node->col == 1) TR = merge(node, TR); 
    else TM = merge(TM, node); 
    if (TM) maketag(TM, 0, 1); 
    root = merge(root, merge(TM, TR)); 
    findEmpty(root); Erase(); 
}
// 0 区间左端点 -1，1 区间右端点 -1
inline void opt5(int l, int r) {
    --r; Node *TM, *TR, *node; 
    split2(root, l - 1, root, TM); split1(TM, r, TM, TR); 
    split1(TM, l, node, TM); 
    if (node && node->col == 0) root = merge(root, node); 
    else TM = merge(node, TM); 
    split2(TM, r - 1, TM, node); 
    if (node && node->col == 1) {
        if (node->r > r) TR = merge(node, TR); 
        else {
            TM = merge(TM, node); 
            split1(TR, r + 1, node, TR); 
            TM = merge(TM, node); 
        }
    } else TM = merge(TM, node); 
    if (TM) maketag(TM, 0, -1); 
    root = merge(root, merge(TM, TR)); 
    findEmpty(root); Erase(); 
}
// 0 区间右端点 +1，1 区间左端点 +1
inline void opt6(int l, int r) {
    ++l; Node *TM, *TR, *node; 
    split2(root, l - 1, root, TM); split1(TM, r, TM, TR); 
    split1(TM, l, node, TM); 
    if (node && node->col == 1) {
        if (node->l < l) root = merge(root, node); 
        else {
            TM = merge(node, TM); 
            split2(root, l - 2, root, node); 
            TM = merge(node, TM); 
        }
    } else TM = merge(node, TM); 
    split2(TM, r - 1, TM, node); 
    if (node && node->col == 0) TR = merge(node, TR); 
    else TM = merge(TM, node); 
    if (TM) maketag(TM, -1, 0); 
    root = merge(root, merge(TM, TR)); 
    findEmpty(root); Erase(); 
}
inline int opt7(int l, int r) {
    Node *TM, *TR, *node; 
    split2(root, l - 1, root, TM); split1(TM, r, TM, TR); 
    int ans = 0; 
    if (TM) ans += TM->sum; 
    split1(TM, l - 1, node, TM); 
    if (node) ans -= node->col * (l - node->l); 
    TM = merge(node, TM); 
    split2(TM, r, TM, node); 
    if (node) ans -= node->col * (node->r - r); 
    TM = merge(TM, node); 
    root = merge(root, merge(TM, TR)); 
    return ans; 
}

int n, m; 
int a[3000005]; 

int main(void) {
    n = read(), m = read(); 
    for (int i = 1; i <= n; ++i) a[i] = read(); 
    int lst = 1; 
    for (int i = 2; i <= n; ++i) if (a[i] != a[i - 1]) root = merge(root, newNode(a[i - 1], lst, i - 1)), lst = i; 
    root = merge(root, newNode(a[n], lst, n)); 
    // PTREE(root); 
    for (lst = 0; m--; ) {
        int op = read(), l = read() ^ lst, r = read() ^ lst; 
        if (op == 1) cover(l, r, 0); 
        else if (op == 2) cover(l, r, 1); 
        else if (op == 3) opt3(l, r); 
        else if (op == 4) opt4(l, r); 
        else if (op == 5) opt5(l, r); 
        else if (op == 6) opt6(l, r); 
        else print(lst = opt7(l, r)), putchar('\n'); 
        // PTREE(root); lst = 0; 
    }
    return 0; 
}