抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

复杂结构上的 DP 问题

更新于 2023年10月30日

11.4k 字

55 分钟

次浏览

本文已经更新完毕，若有错误或需要补充的内容请在评论区留言。

之前的 DP 都是在线性结构上进行的，实际上 DP 还可以在树上或者 DAG 上进行。本文将对这些内容进行简单的介绍。

更新日志

2023/10/30

更新了少许杂题。

树形 DP

树形 DP 就是将在线性结构上的 DP 变到了树上。

概念

既然 DP 都长到树上去了，那么肯定有不一样的地方。

由于树固有的递归性质，树形 DP 一般都是递归进行的。在树形 DP 中，我们会选根节点为 DP 的开始，然后对于它的每棵子树进行递归，然后考虑转移。递归到了一个叶子节点，就可以进行初始化了。

基础例题

之所以大多数教程都直接上题，是因为这玩意没法讲！
之前说了树形 DP 就是在树上进行 DP，就是把状态的转移移到了树上。但这么说没人能听得懂，所以我们只能通过题目来学习，那么就来吧。

[Luogu P1352] 没有上司的舞会

Portal.

某大学有 nn 个职员，编号为 1…n1\ldots n。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 rir_i,但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。计算邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

根据刚才的讲解和在线性 DP 中的经验，我们可以设 f[x]f[x] 为 xx 的子树的最大的快乐指数。

但这样不行，我们需要知道 xx 是否参加舞会，来判断 xx 的上司是否能参加舞会。
那么根据在线性 DP 中讲过的“打不过就加入”，我们可以设 f[x][0]f[x][0] 为 xx 不参加舞会，f[x][1]f[x][1] 为 xx 参加舞会。

那么根据题意，便有转移：

f[x][0]=∑s∈son[x]max⁡(f[x][0],f[x][1])f[x][0] = \sum\limits_{s\in son[x]}\max(f[x][0], f[x][1])

f[x][1]=r[x]+∑s∈son[x]f[x][0]f[x][1] = r[x] + \sum\limits_{s\in son[x]}f[x][0]

那么代码就很容易写出来了：

查看代码 
#include <bits/stdc++.h>
using namespace std;

inline int read(void)
{
    int x = 0, c = getchar(), f = 1;
    while (!isdigit(c)) {if (c == '-') f = -1; c = getchar();}
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x * f;
}

int n;
int r[6005];
bool v[6005];
vector <int> son[6005];
int f[6005][2];

void dp(int o)
{
    f[o][0] = 0; // 不参加，初始为 0
    f[o][1] = r[o]; // 参加，初始为 r[o]
    for (int i = 0; i < son[o].size(); ++i) // 遍历所有子树
    {
        int y = son[o][i];
        dp(y); // 递归进行
        f[o][0] += max(f[y][0], f[y][1]); // 可以参加或不参加
        f[o][1] += f[y][0]; // 只能不参加
    }
}

int main(void)
{
    n = read();
    for (int i = 1; i <= n; ++i) r[i] = read();
    for (int i = 1; i < n; ++i)
    {
        int x = read(), y = read();
        v[x] = 1;
        son[y].push_back(x);
    }
    int root;
    for (int i = 1; i <= n; ++i)
        if (!v[i])
        {
            root = i; // 寻找根节点开始 DP
            break;
        }
    dp(root);
    cout << max(f[root][0], f[root][1]) << endl; // 要取最大值
    return 0;
}

状态有 O(n)O(n) 个，每个状态在转移时都会被考虑一次，因此时间复杂度为 O(n)O(n)。

树形 DP 还有另一种实现方式：以拓扑序自底向上迭代，速度比上述递归方法快一点，但实用性不高。感兴趣的读者可以自行了解。

[Luogu P2016] 战略游戏

Portal.

n(n≤1500)n(n\le 1500) 的树。他要在这棵树的结点上放置最少数目的士兵，使得这些士兵能了望到所有的路。他要在这棵树的结点上放置最少数目的士兵，使得这些士兵能了望到所有的路。

这道题和上道很相似，但可以注意到这是一棵无根树。而想要做树形 DP，就必须有根。
那怎么办呢？转成有根树就行了。随便找一个结点作根，代码如下：

for (int i = 0; i < n; ++i)
{
    int o = read(), k = read();
    for (int j = 0; j < k; ++j)
    {
        int t = read();
        G[o].push_back(t);
        G[t].push_back(o);
    }
}
v[0] = -1;
dfs(0);

这里的 vv 数组代表 v[o]v[o] 的父亲。dfs(o) 代表遍历节点 oo。

dfs 的过程如下：

void dfs(int o)
{
    done[o] = 1;
    for (int i = 0; i < G[o].size(); ++i)
    {
        if (done[G[o][i]] == 0)
        {
            son[o].push_back(G[o][i]);
            v[G[o][i]] = o;
            dfs(G[o][i]);
        }
    }
}

这里用了一个 done 数组来防止重复遍历，还有一种方式如下：

void dfs(int o, int fa)
{
    for (int i = 0; i < G[o].size(); ++i)
        if (G[o][i] != fa)
        {
            son[o].push_back(G[o][i]);
            dfs(G[o][i], o);
        }
}

为什么可以这样做呢？因为加的是无向边，来回遍历时才会造成重复遍历。

我们设 f(i,0)f(i,0) 代表在 ii 的位置上不放士兵，f(i,1)f(i,1) 代表在 ii 的位置上放士兵，它们的子树所需要的最少士兵。

那么完整代码就很容易写出来了：

查看代码 
#include <iostream>
#include <cstdio>
#include <vector>

using namespace std;

inline int read(void)
{
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int n;
int f[1505][2];
bool done[1505];
vector <int> son[1505];
vector <int> G[1505];

void dfs(int o, int fa)
{
    done[o] = 1;
    for (int i = 0; i < G[o].size(); ++i)
        if (done[G[o][i]] == 0)
        {
            son[o].push_back(G[o][i]);
            dfs(G[o][i], o);
        }
}

void dp(int o)
{
    f[o][0] = 0;
    f[o][1] = 1;
    for (int i = 0; i < son[o].size(); ++i)
    {
        int y = son[o][i];
        dp(y);
        f[o][0] += f[y][1]; // 必须放
        f[o][1] += min(f[y][0], f[y][1]); // 可放可不放
    }
}

int main(void)
{
    n = read();
    for (int i = 0; i < n; ++i)
    {
        int o = read(), k = read();
        for (int j = 0; j < k; ++j)
        {
            int t = read();
            G[o].push_back(t);
            G[t].push_back(o);
        }
    }
    dfs(0, -1);
    dp(0);
    cout << min(f[0][0], f[0][1]) << endl;
    return 0;
}

[Luogu P1122] 最大子树和

Portal.

这跟上一题很相似，但是我们可以不建树，直接在 DP 的时候判断是否来自 fa 即可。求最大子树和，只需要将正的子树加上即可。

查看代码 
#include <iostream>
#include <cstdio>
#include <vector>

using namespace std;

int n;
int a[16005], f[16005];
vector <int> G[16005];

void dp(int o, int fa)
{
    f[o] = a[o];
    for (int i = 0; i < G[o].size(); ++i)
    {
        int y = G[o][i];
        if (y == fa) continue;
        dp(y, o);
        if (f[y] > 0) f[o] += f[y];
    }
}

int main(void)
{
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i);
    for (int i = 1; i < n; ++i)
    {
        int u, v;
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    dp(1, 0);
    int ans = -2e9;
    for (int i = 1; i <= n; ++i)
        ans = max(ans, f[i]);
    printf("%d\n", ans);
    return 0;
}

关于树形 DP 有一个问题：为什么我们可以随便选一个点作为根节点进行 DP 呢？这是因为在考虑子树的过程中，如果一个以 root 节点为根的答案会更好，它要么相当于一棵子树，要么相当于它的一个孙辈的子树。

当然也有例外，我们很快就会见到。

[ZJOI2007] 时态同步

Portal.

n(n≤105)n(n\le 10^5) 个点的有根树，有边权，一次操作可以将某条边的边权 +1+1。求最少使用多少次操作，可以让所有叶子结点到根的距离相同。

很容易想到一个贪心做法：优先调整靠上的边。为什么？因为与其在叶子节点的边权都 +1+1，不如直接在父亲节点的边 +1+1。这样，一个节点只需要调整它的子树，保证它的子树边权相同即可，剩下的交给它的父亲。

那我们记 f(x)f(x) 为调整好 xx 的子树的最少操作数。但是想要成功计算，我们还需要知道节点到叶子节点的距离，所以我们记 g(x)g(x) 为调整后 xx 到它的最底层的叶子节点的距离。

转移也不难。很容易得出 g(x)g(x) 的转移：

g(x)=max⁡y∈son(x){g[y]+wx,y}g(x)=\max\limits_{y\in son(x)}\left\{g[y]+w_{x,y}\right\}

f(x)f(x) 怎么转？像这样：

f(x)=∑y∈son(x)(f(y)+(g(x)−g(y)−wx,y))f(x)=\sum\limits_{y\in son(x)}(f(y)+(g(x)-g(y)-w_{x,y}))

什么意思？首先肯定要加上调整所有子树的代价，然后要开始调整这些子树。代价是多少？显然是 g(x)−g(y)−wx,yg(x)-g(y)-w_{x,y}，也就是当前的深度剪去叶子节点的深度再减去这条边的长度。

代码如下：

查看代码 
#include <iostream>
#include <cstdio>
#include <vector>

#define pii pair<int, int>
#define Y first
#define W second

using namespace std;
using i64 = long long;

inline int read(void)
{
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int n, s;
i64 f[500005], g[500005];
vector <pii> son[500005];

struct edge
{
    int from, to, dist;
    edge(int u, int v, int d) :
        from(u), to(v), dist(d) {}
};
vector <edge> edges;
vector <int> G[500005];

inline void addedge(int u, int v, int d)
{
    edges.push_back(edge(u, v, d));
    G[u].push_back(edges.size() - 1);
}

void dp(int x)
{
    // 0 就是初始条件，叶子节点不需要调整
    for (int i = 0; i < son[x].size(); ++i)
        dp(son[x][i].Y); // 对儿子进行处理
    for (int i = 0; i < son[x].size(); ++i)
        g[x] = max(g[x], g[son[x][i].Y] + son[x][i].W); // g 的转移
    for (int i = 0; i < son[x].size(); ++i)
        f[x] += f[son[x][i].Y] + (g[x] - g[son[x][i].Y] - son[x][i].W); // f 的转移
}

void dfs(int o, int fa)
{
    for (int i = 0; i < G[o].size(); ++i)
    {
        edge &e = edges[G[o][i]];
        if (e.to != fa)
        {
            son[o].push_back(make_pair(e.to, e.dist));
            dfs(e.to, o);
        }
    }
}

int main(void)
{
    n = read(), s = read();
    for (int i = 1; i < n; ++i)
    {
        int u = read(), v = read(), d = read();
        addedge(u, v, d);
        addedge(v, u, d);
    }
    dfs(s, -1); // 建树
    dp(s);
    printf("%lld\n", f[s]);
    return 0;
}

[ZJOI2006] 三色二叉树

Portal.

设 f(i,0),f(i,1),f(i,2)f(i,0),f(i,1),f(i,2) 分别代表 ii 节点染成绿色、红色、蓝色的绿色节点最多数。转移对于读到这的读者来说应该不是困难。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int n;
char s[500005];
int f[500005][3], g[500005][3]; // f 最多，g 最少，0~2: GRB 的绿色节点

void dp(int o)
{
    if (s[o] == '0')
    {
        f[o][0] = g[o][0] = 1;
        return;
    }
    int x, y;
    dp(x = ++n);
    if (s[o] == '1')
    {
        f[o][0] = max(f[x][1], f[x][2]) + 1;
        f[o][1] = max(f[x][0], f[x][2]);
        f[o][2] = max(f[x][0], f[x][1]);

        g[o][0] = min(g[x][1], g[x][2]) + 1;
        g[o][1] = min(g[x][0], g[x][2]);
        g[o][2] = min(g[x][0], g[x][1]);
    }
    else
    {
        dp(y = ++n);
        f[o][0] = max(f[x][1] + f[y][2], f[x][2] + f[y][1]) + 1;
        f[o][1] = max(f[x][0] + f[y][2], f[x][2] + f[y][0]);
        f[o][2] = max(f[x][0] + f[y][1], f[x][1] + f[y][0]);

        g[o][0] = min(g[x][1] + g[y][2], g[x][2] + g[y][1]) + 1;
        g[o][1] = min(g[x][0] + g[y][2], g[x][2] + g[y][0]);
        g[o][2] = min(g[x][0] + g[y][1], g[x][1] + g[y][0]);
    }
}

int main(void)
{
    scanf("%s", s + 1);
    dp(++n);
    printf("%d %d\n", max({f[1][0], f[1][1], f[1][2]}), min({g[1][0], g[1][1], g[1][2]}));
    return 0;
}

[UVa 12186] Another Crisis

Portal.

状态的定义与转移对于读者来说应该已经不是困难，这里提供另一种实现。由于需要排序，所以将 dp 做成有返回值的函数，这样其实更类似于 dfs。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int n, t, f[100005];
vector <int> son[100005];

int dp(int x)
{
    if (son[x].empty()) return 1;
    vector <int> a;
    for (int i = 0; i < son[x].size(); ++i)
        a.push_back(dp(son[x][i]));
    sort(a.begin(), a.end());
    int c = ceil(son[x].size() * t / 100.0);
    int ans = 0;
    for (int i = 0; i < c; ++i)
        ans += a[i];
    return ans;
}

int main(void)
{
    while (scanf("%d%d", &n, &t) == 2 && n)
    {
        for (int i = 0; i <= n; ++i) 
        {
            son[i].clear();
            f[i] = 0;
        }
        for (int i = 1, x; i <= n; ++i)
        {
            scanf("%d", &x);
            son[x].push_back(i);
        }
        printf("%d\n", dp(0));
    }
    return 0;
}

[UVa 1218] Perfect Service

Portal.

这种题有属于自己的套路：

  • f(x,0)f(x,0) 代表 xx 是服务器，那么儿子随便；
  • f(x,1)f(x,1) 代表 xx 不是，但是父亲是，那么儿子都不是；
  • f(x,2)f(x,2) 代表 xx 和父亲都不是，但是有一个儿子是。

转移方程应该不难写出。

查看代码 
#include <iostream>
#include <cstdio>
#include <vector>

using namespace std;
const int INF = 10001;

int n, f[10005][3];
vector <int> G[10005];

void dp(int x, int fa)
{
    f[x][0] = 1, f[x][1] = 0, f[x][2] = INF;
    int sum = 0;
    for (auto y : G[x])
    {
        if (y == fa) continue;
        dp(y, x);
        f[x][0] += min(f[y][0], f[y][1]);
        f[x][1] += f[y][2];
        sum += f[y][2];
    }
    for (auto y : G[x])
        if (y != fa) f[x][2] = min(f[x][2], sum - f[y][2] + f[y][0]);
}

int main(void)
{
    while (n != -1 && scanf("%d", &n) == 1)
    {
        for (int i = 1; i <= n; ++i) G[i].clear();
        for (int i = 1; i < n; ++i)
        {
            int u, v;
            scanf("%d%d", &u, &v);
            G[u].push_back(v);
            G[v].push_back(u);
        }
        dp(1, 0);
        printf("%d\n", min(f[1][0], f[1][2]));
        scanf("%d", &n);
    }
    return 0;
}

树形背包

问题定义在树形结构上，依照子树设定子问题。常常用 f(x,s)f(x,s) 表示子树 xx 在状态限制 ss 下的最优解。先递归求解子树的答案，再计算当前结点答案。

普通的背包，如 01 背包可以放到树上，而树形结构还可以用来解决依赖性背包。

普通背包 | [Luogu P2015] 二叉苹果树

Portal.

有一棵苹果树，如果树枝有分叉，一定是分二叉（就是说没有只有一个儿子的结点）

这棵树共有 NN 个结点（叶子点或者树枝分叉点），编号为 1∼N1 \sim N，树根编号一定是 11。

我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有 44 个树枝的树：

2   5
 \ / 
  3   4
   \ /
    1

现在这颗树枝条太多了，需要剪枝。但是一些树枝上长有苹果。

给定需要保留的树枝数量，求出最多能留住多少苹果。

我们设 f(i,j)f(i,j) 代表以 ii 为根的子树，恰好保留 jj 条边所能获得的最多苹果数。那么我们考虑左右子树（如果有），由于 f(x,0)f(x,0) 这个状态是存在的，所以我们让 −1-1 的体积代表什么都不选。

下面是代码，请仔细阅读。

#include <iostream>
#include <cstdio>

using namespace std;

int n, q;
int son[105][2], val[105][2];
int s[105]; // s[x] 为 x 及其子节点所含有的边数
int f[105][105];

void dp(int o)
{
    int x = son[o][0], y = son[o][1];
    if (!x) return;
    dp(x), dp(y);
    s[o] = s[x] + s[y] + 2; // +2 是连接左右子树用掉的
    for (int i = -1; i <= s[x]; ++i)
        for (int j = -1; j <= s[y]; ++j)
        {
            int vl = (i == -1 ? 0 : f[x][i] + val[o][0]); // -1 不选就是 0，选了就是儿子的能获得的苹果数值加上儿子上的苹果数（因为这一条边选了）
            int vr = (j == -1 ? 0 : f[y][j] + val[o][1]);
            f[o][i + j + 2] = max(f[o][i + j + 2], vl + vr); // i + j 是左子树和右子树用掉的边，+2 是当前节点连接左右子树用掉的边
        }
}

int main(void)
{
    scanf("%d%d", &n, &q);
    for (int i = 1; i < n; ++i)
    {
        int x;
        scanf("%d", &x);
        int b = son[x][0] > 0; // 存在左子树就往右子树里读入
        scanf("%d%d", &son[x][b], &val[x][b]); // 这里的树枝上的苹果送给儿子
    }
    dp(1);
    printf("%d\n", f[1][q]);
    return 0;
}

可以发现，其实这就是一个 01 背包问题，只不过跑到了树上。

依赖性背包 | [CTSC1997] 选课

Portal.

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有 NN 门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程 a 是课程 b 的先修课即只有学完了课程 a，才能学习课程 b）。一个学生要从这些课程里选择 MM 门课程学习，问他能获得的最大学分是多少？

在《背包》中我们就讨论过这个问题，不过当时我们给出的方案是暴力枚举子集转换成分组背包，但是显然很慢。现在有了树，这类问题就变的好解了。

如果没有先修课的限制，这就是一个标准的 01 背包问题。由于每门课程的先修课只有一门，这就构成了一棵每门课都以自己的先修课为父亲的森林结构（因为可能会有多门课没有先修课）。既然如此，我们增设一个虚（chao）拟（ji）课（ba）程（ba），0 号节点，作为”实际上没有先修课的课程“。

设 f(x,t)f(x,t) 表示在以 xx 为根的子树中选 tt 门课程能获得的最高学分。设它的子节点个数为 pp，那么有 f(x,0)=0f(x,0)=0。当 t>0t>0 时，必须选节点 xx，那么有（score[x]score[x] 指课程 xx 获得的学分，yiy_i 指 xx 的子节点）：

f(x,t)=max⁡∑i=1pci=t−1{∑i=1pf(yi,ci)}+score[x]f(x,t)=\max\limits_{\sum_{i=1}^{p} c_i=t-1}\left\{\sum\limits_{i=1}^{p}f(y_i,c_i)\right\}+score[x]

也就是说，要在满足子节点所选的科目的综合为 (∑i=1pci)=t−1\left(\sum_{i=1}^{p} c_i\right)=t-1 的前提下，在子树中选课获得最大的得分。

现在想一想，这就是分组背包的处理方式！

可以这么理解。对于每个节点，有 pp 个儿子，也就是有 pp 组物品，每组物品都有 t−1t-1 个（不足的用体积和价值都为 00 的物品来补齐），其中第 ii 组的第 jj 个物品体积为 jj，价值为 f(yi,j)f(y_i,j)。背包的总容量为 t−1t-1（因为当前节点会吃掉体积为 11 的容量）。
每组中至多只能选一个物品（难不成你还能同时选 f(yi,0)f(y_i,0) 和 f(yi,1)f(y_i,1) 吗 ），使得物品体积不超过 t−1t-1 的前提下（根据之前背包中所推的原理，不需要取体积分别为 0∼t−10\sim t-1 的最大值），物品价值最大（获得最多的学分）。然而我们的超级爸爸 00 号节点除外，因为它根本不需要被选修，背包总容积为 tt。

实现时我们可以装作有 m+1m+1 个可选的物品，这样就不用理会超级爸爸了。下面是代码，请仔细阅读。

#include <bits/stdc++.h>
using namespace std;

int n, m, s[305], siz[305];
int f[305][305];
vector <int> son[305];

void dp(int x)
{
    f[x][0] = 0; f[x][1] = s[x]; siz[x] = 1;
    for (int y : son[x])
    {
        dp(y); // 递归求解每个物品的价值（每个儿子的价值）
        for (int i = min(siz[x], m + 1); i >= 1; --i)
            for (int j = min(siz[y], m + 1 - i); j >= max(1, i - siz[x]); --j)
                f[x][i + j] = max(f[x][i + j], f[x][i] + f[y][j]);
        siz[x] += siz[y];
    }
}

int main(void)
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i)
    {
        int x; scanf("%d", &x);
        son[x].push_back(i);
        s[i] = read();
    }
    memset(f, 0xff, sizeof(f)); // 求的是最大值
    dp(0); // 从超级节点开始 dp
    printf("%d\n", f[0][m + 1]); // 必选，所以答案只能是这一个
    return 0;
}

树形背包中的上下界需要注意，需要卡死，注意不要遍历到无用的状态，一定是一个将子树合并到当前节点的过程，这样才能保证时间复杂度为 O(nm)O(nm)，大致原理是：“每对节点只会恰好在 LCA 处合并一次”。

换根 DP

POJ3585 Accumulation Degree。

正常来讲，这道题怎么做？很显然，不能随便选一个点作为根节点，这样无法统计答案。如果枚举源点，那么每次都跑一个树形 DP 就可以解决了，但是时间不允许。但是不要紧，一种名为“二次扫描与换根法”的技巧可以只 DP 一次来统计答案，也被称之为换根 DP。在此之前，我们先把 nn 次 DP 的转移方程写出来：

f(x)=∑y∈Son(x){min⁡{f(y),c(x,y)},deg[x]>1,c(x,y),deg[x]=1.f(x) = \sum_{y\in Son(x)} \begin{cases} \min\{f(y), c(x, y)\}&, deg[x]>1,\\ c(x,y)&, deg[x] = 1. \end{cases} 

void dp(int x, int fa)
{
    f[x] = 0;
    for (int i = 0; i < G[x].size(); ++i)
    {
        int y = G[x][i].to, w = G[x][i].val;
        if (y != fa)
        {
            dp(y, x);
            if (deg[y] == 1) f[x] += w;
            else f[x] += min(f[y], w);
        }
    }
}

我们任意选择一个节点作为 root 进行如上操作后，就可以开始换根了：

设 g(x)g(x) 代表以 xx 作为源点，流向整个水系，流量最大是多少。初始肯定是 g(root)=f(root)g(root)=f(root)。

如果 g(x)g(x) 已经被求出，那么对于子节点 yy，g(y)g(y) 包含两个部分：

  1. 从 yy 流入 yy 的子树的流量，就是 f(y)f(y)；
  2. 从 yy 到父亲 xx 然后继续流的流量。

这个 22 怎么求？还记得我们是怎么求解树的重心的吗？我们用整体的减去了局部的，就等于除了局部以外的内容了。

这里也是一样，像这样：

g(y)=f(y)+{min⁡{g(x)−min⁡{f(y),c(x,y)},c(x,y)},deg[x]>1c(x,y),deg[x]=1g(y)=f(y)+\begin{cases} \min\left\{g(x)-\min\left\{f(y),c(x,y)\right\}, c(x,y)\right\}&,deg[x]>1\\ c(x,y)&,deg[x]=1 \end{cases}

当 yy 的父亲 xx 是个度数为 11 的点时，它就是一个汇点，流量就是 c(x,y)c(x,y)；当它不是一个汇点的时候，就等于以它父亲作为源点的整个水系的流量 g(x)g(x)，减去从 x→yx\rightarrow y 的流量 min⁡{f(y),c(x,y)}\min\{f(y),c(x,y)\}，同时还要将这个差与 c(x,y)c(x,y) 取最小值。

#include <bits/stdc++.h>
using namespace std;

struct edge {
    int to, val;
    edge(int to = 0, int val = 0) :
        to(to), val(val) {}
};

int n;
int f[200005], g[200005], deg[200005];
vector <edge> G[200005];

inline void addedge(int u, int v, int w) { G[u].push_back(edge(v, w)); }

void dp(int x, int fa) {
    f[x] = 0;
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i].to, w = G[x][i].val;
        if (y != fa) {
            dp(y, x);
            if (deg[y] == 1) f[x] += w;
            else f[x] += min(f[y], w);
        }
    }
}

void dfs(int x, int fa) {
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i].to, w = G[x][i].val;
        if (y != fa) {
            if (deg[x] == 1) g[y] = f[y] + w; // 先计算好当前的 g，然后再遍历
            else g[y] = f[y] + min(g[x] - min(f[y], w), w);
            dfs(y, x);
        }
    }
}

void solve(void) {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) G[i].clear();
    memset(deg, 0, sizeof(deg));
    memset(f, 0, sizeof(f));
    memset(g, 0, sizeof(g));
    for (int i = 1; i < n; ++i) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        addedge(u, v, w), addedge(v, u, w);
        deg[u]++, deg[v]++;
    }
    dp(1, -1);
    g[1] = f[1];
    dfs(1, -1);
    int ans = 0;
    for (int i = 1; i <= n; ++i)
        ans = max(ans, g[i]);
    printf("%d\n", ans);
}

int main(void) {
    int T;
    scanf("%d", &T);
    while (T--) solve();
    return 0;
}

也就是说，在换根的过程中，要搞明白代价少了什么，又多了什么。

图上 DP

我们说过，DP 需要有无后效性。所以一般我们只能在 DAG 上进行 DP（后面会学习到高斯消元可以进行后效性处理）。当然，不太复杂的问题，如单个环上的问题上的问题也是可以做的。或者，一般图的缩点之后也可以做。

DAG 上的 DP

你有没有想过 DP 的本质是什么？

简述

线性结构上的 DP 也好，树形结构上的 DP 也罢。它们都有“状态””决策”两个概念。状态对应图上的一个点，而决策对应图上的边。

你有没有发现什么？

如果 DP 的状态图长成下图这样，会发生什么？

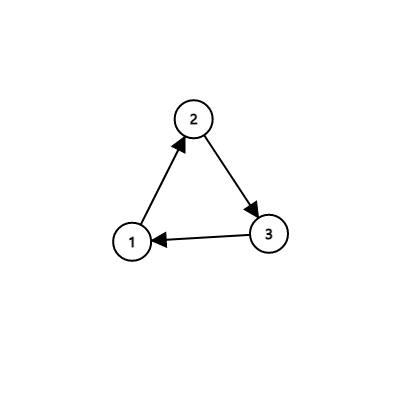
image

想要求解状态 33，依赖于状态 22，而状态 22 依赖于状态 11，状态 11 又依赖于状态 33！这成了个无限循环问题。

所以可以得出结论，DP 一般只适用于有向无环图（DAG），遍历顺序便是这个 DAG 的一个拓扑序。如果这个图是带环的，那么一般它就不能 DP。

一个问题可以 DP，是因为这个问题可以从小问题的解，推断出大问题的解。我们可以从初始状态的解，推出最终状态的解，从而解决问题。也就是说有这几条性质：

如果我们按以上方法绘图，那么立即就有几条性质：

  1. DP 的每一个状态都对应着一个点；
  2. 每种可能的转移方式，都对应着一条有向边；
  3. DP 的求解顺序，等同于这张图上的拓扑排序；
  4. 整张图必须是 DAG，否则不可能找到合适的求解顺序。

[Luogu P1613] 跑路

Portal.

我们的目的就是建图，然后求最短路。令 G[i,j,k]=1G[i,j,k]=1 代表存在一条 i→ji\rightarrow j，长度为 2k2^k 的边，这样的边就是可以 1s1s 跑完的。那么若 G[i,t,k−1]=G[t,j,k−1]=1G[i,t,k-1]=G[t,j,k-1]=1，则 G[i,j,k]=1G[i,j,k]=1。由于图的规模很小，求最短路时直接使用 Floyd 即可。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int n, m;
int f[55][55];
bool G[55][55][40];

int main(void) {
    scanf("%d%d", &n, &m);
    memset(f, 0x3f, sizeof f);
    while (m--) {
        int u, v;
        scanf("%d%d", &u, &v);
        f[u][v] = 1;
        G[u][v][0] = true;
    }
    for (int l = 1; l <= 32; ++l)
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= n; ++j)
                for (int k = 1; k <= n; ++k)
                    if (G[i][j][l - 1] && G[j][k][l - 1]) {
                        G[i][k][l] = true;
                        f[i][k] = 1;
                    }
    for (int k = 1; k <= n; ++k)
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= n; ++j)
                f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
    printf("%d\n", f[1][n]);
    return 0;
}

环上 DP

可以考虑使用缩点解决。

Problemset

可能比较麻烦，但都没有什么难度。

树形 DP

基础的树形 DP，后面的题会稍微难一点。

[SDOI2006] 保安站岗

Portal.

设 f(x,0),f(x,1),f(x,2)f(x,0),f(x,1),f(x,2) 分别代表由父亲、自己和儿子来维护。需要注意的就是由儿子维护的，儿子要至少有一个是自己维护自己的。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int n;
int w[1505], f[1505][3];
vector <int> G[1505];

void dp(int x, int fa)
{
    f[x][1] = w[x];
    int flag = 0, minn = 1e9;
    for (int i = 0; i < G[x].size(); ++i)
    {
        int y = G[x][i];
        if (y != fa)
        {
            dp(y, x);
            f[x][0] += min({f[y][1], f[y][2]});
            f[x][1] += min({f[y][0], f[y][1], f[y][2]});
            if (f[y][1] < f[y][2]) f[x][2] += f[y][1], flag = true;
            else minn = min(minn, f[y][1] - f[y][2]), f[x][2] += f[y][2];
        }
    }
    if (!flag) f[x][2] += minn;
}

int main(void)
{
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
    {
        int p, t, x;
        scanf("%d", &p);
        scanf("%d%d", w + p, &t);
        while (t--)
        {
            scanf("%d", &x);
            G[p].push_back(x), G[x].push_back(p);
        }
    }
    dp(1, 0);
    printf("%d\n", min(f[1][1], f[1][2]));
    return 0;
}

[CSP-S2019] 括号树

Portal.

f(i)f(i) 表示 ii 到 11 的答案，再记 g(i)g(i) 为第 ii 个节点的贡献，如果扫描到当前一个 )，就说明这个节点是有贡献的。维护一个记录左括号位置的栈，扫描到一个 ) 就从栈中进行匹配，更新 g(x)=g(k)+1g(x)=g(k)+1，其中 kk 为弹出的栈顶的父亲，这样可以将父亲的贡献值也算上。如果是 ( 就直接入栈。这时候就可以计算当前的答案：父亲节点的答案加上当前节点的贡献。接下来就可以递归计算儿子的贡献，然后要还原现场使得父亲的其它儿子可以正确计算：如果弹出过栈就要把这个再压回去，否则如果发现栈不是空的，就是压进去过元素，把它 pop 出来。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;

int n, fa[500005];
i64 ans = 0, f[500005], g[500005]; // g[i] 表示节点 i 的贡献
char s[500005];
vector <int> son[500005];
stack <int> v;

void dp(int x)
{
    int tmp = -1;
    if (s[x] == ')')
    {
        if (!v.empty())
        {
            tmp = v.top();
            g[x] = g[fa[tmp]] + 1;
            v.pop();
        }
    }
    else v.push(x);
    f[x] = f[fa[x]] + g[x];
    for (int i = 0; i < son[x].size(); ++i)
        dp(son[x][i]);
    if (tmp != -1) v.push(tmp); // 压回去
    else if (!v.empty()) v.pop(); // 还原现场，将压入的 '(' pop 出来
}

int main(void)
{
    scanf("%d%s", &n, s + 1);
    for (int i = 2, x; i <= n; ++i)
        scanf("%d", &x), son[x].push_back(i), fa[i] = x;
    dp(1);
    for (int i = 1; i <= n; ++i)
        ans ^= f[i] * i;
    printf("%lld\n", ans);
    return 0;
}

[CF486D] Valid Sets

Portal.

发现需要枚举点来统计信息，但是换根 DP 不是很好做，而且数据范围很小，所以考虑枚举每个点然后进行暴力 DP。

我们枚举每一个点，并令它是点权最大的点。设 f(x)f(x) 代表包含 xx 的子树的最大连通块数。如果儿子 yy 的点权差大于了 dd 不行，如果点权比 rootroot 大也不行，相等的时候要判断一下点的编号，只能计算一个，因为枚举 yy 的时候它还会被计算一遍。

转移也很简单，要乘上子树的大小 +1，设子树的大小为 size(x)size(x)，对应选 0∼size(y)0\sim size(y)。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;
const int MOD = 1000000007;

int n, d;
int a[2005], f[2005];
vector <int> G[2005];
inline void addedge(int u, int v) { G[u].push_back(v); }

void dp(int x, int fa, int root) {
    f[x] = 1;
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i];
        if (y == fa) continue;
        if (a[y] > a[root] || (a[y] == a[root] && y < root)) continue;
        if (a[root] - a[y] > d) continue;
        dp(y, x, root);
        f[x] = 1ll * f[x] * (f[y] + 1) % MOD;
    }
}

int main(void) {
    scanf("%d%d", &d, &n);
    for (int i = 1; i <= n; ++i)
        scanf("%d", a + i);
    for (int i = 1, u, v; i < n; ++i) {
        scanf("%d%d", &u, &v);
        addedge(u, v), addedge(v, u);
    }
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        memset(f, 0, sizeof(f));
        dp(i, 0, i);
        ans = (ans + f[i]) % MOD;
    }
    printf("%d\n", ans);
    return 0;
}

[国家集训队] 聪聪可可

Portal.

设 f(x,i)f(x,i) 代表距离 xx 为 ii（模意义）的点数，按照类似于点分治的方式统计即可。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int gcd(int x, int y) {
    if (y == 0) return x;
    return gcd(y, x % y);
}

int n, ans, f[20005][3];
vector<pair<int, int>> G[20005];
int M(int x) { return (x % 3 + 3) % 3; }

void dfs(int x, int fa) {
    f[x][0] = 1;
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i].first, w = G[x][i].second;
        if (y == fa) continue;
        dfs(y, x);
        for (int i = 0; i < 3; ++i) ans += f[y][i] * f[x][M(-i - w)] * 2;
        for (int i = 0; i < 3; ++i) f[x][M(i + w)] += f[y][i];
    }
}

int main(void) {
    scanf("%d", &n);
    for (int i = 1; i < n; ++i) {
        int u, v, d; scanf("%d%d%d", &u, &v, &d);
        G[u].emplace_back(make_pair(v, d));
        G[v].emplace_back(make_pair(u, d));
    }
    dfs(1, 0);
    ans += n; int full = n * n; int g = gcd(ans, full);
    ans /= g, full /= g;
    printf("%d/%d\n", ans, full);
    return 0;
}

[HNOI2003] 消防局的设立

Portal.

令 f(x,0∼4)f(x,0\sim 4) 分别代表 xx 覆盖到它的爷爷，它的父亲，它自己，它的儿子，它的孙子及其子树的最小代价，转移见代码。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int n;
int f[1005][5];
vector <int> G[1005];
inline void addedge(int u, int v) { G[u].push_back(v); }

void dp(int x, int fa)
{
    int tot = 0, sum3 = 0, sum2 = 0;
    for (int i = 0; i < G[x].size(); ++i)
    {
        int y = G[x][i];
        if (y == fa) continue;
        dp(y, x);
        ++tot;
        sum3 += f[y][3]; // 记录儿子自行覆盖它们的儿子所在的子树
        sum2 += f[y][2]; // 记录儿子自行覆盖它所在的子树
    }
    if (tot == 0)
    {
        f[x][0] = f[x][1] = f[x][2] = 1;
        return;
    }
    f[x][0] = 1, f[x][1] = f[x][2] = 1e9; // 只有想要覆盖自己的爷爷是必须要自行执行的，初值为 1
    for (int i = 0; i < G[x].size(); ++i)
    {
        int y = G[x][i];
        if (y == fa) continue;
        // 距离为 2 的点都覆盖了，只需要儿子覆盖它们的孙子即可
        f[x][0] += f[y][4];
        // f[x][1] 的由来：它有一个儿子(y)覆盖到了它的爷爷，可以覆盖它的兄弟，但是无法覆盖到它兄弟的子树（不含自己）
        f[x][1] = min(f[x][1], f[y][0] + sum3 - f[y][3]);
        // f[x][2] 的由来：它有一个儿子(y)覆盖到了它的父亲，但是它的兄弟无法覆盖
        f[x][2] = min(f[x][2], f[y][1] + sum2 - f[y][2]); 
        // 要求它所有的儿子被覆盖，儿子需要覆盖自己和子树
        f[x][3] += f[y][2];
        // 要求它的孙子被覆盖，儿子需要覆盖它们的儿子即可
        f[x][4] += f[y][3];
    }
    for (int i = 1; i < 5; ++i) f[x][i] = min(f[x][i], f[x][i - 1]);
}

int main(void)
{
    scanf("%d", &n);
    for (int i = 2, x; i <= n; ++i)
    {
        scanf("%d", &x);
        addedge(i, x);
        addedge(x, i);
    }
    dp(1, 0);
    printf("%d\n", f[1][2]); // 答案是覆盖自己及子树
    return 0;
}

树上背包

树上背包（分组，依赖性）的模型非常有用，而且类似于 f[x][k]f[x][k] 的状态设计也可以算是广义的树形背包，一定要了解原理。

[Luogu P1273] 有线电视网

Portal.

就是选课的翻版，设 f(i,j)f(i,j) 代表以 ii 为根的子树中，满足了 jj 个客户的最大收益。然后直接 DP 做就行。注意最多能满足的客户个数。

查看代码 
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#define pii pair<int, int>

using namespace std;

int n, m, f[3005][3005]; // f[i][j] 以 i 为根的子树中，j 个客户转的最大收益
int M[3005];
vector <pii> G[3005];

int dp(int x) { // 返回观众的个数
    f[x][0] = 0;
    if (x > n - m) return 1;
    int sum = 0;
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i].first, w = G[x][i].second;
        sum += dp(y);
        for (int j = sum; j >= 0; --j)
            for (int k = j; k >= 0; --k)
                f[x][j] = max(f[x][j], f[x][j - k] + f[y][k] - w);
    }
    return sum;
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n - m; ++i) {
        int k;
        scanf("%d", &k);
        while (k--) {
            int a, c;
            scanf("%d%d", &a, &c);
            G[i].push_back({a, c});
        }
    }
    memset(f, 0xbf, sizeof(f));
    for (int i = n - m + 1; i <= n; ++i) scanf("%d", &f[i][1]);   
    dp(1);
    for (int i = m; i >= 0; --i)
        if (f[1][i] >= 0) {
            printf("%d\n", i);
            break;
        }
    return 0;
}

[Luogu P1272] 重建道路

Portal.

一场可怕的地震后，人们用 NN 个牲口棚（编号 1∼N1\sim N）重建了农夫 John 的牧场。由于人们没有时间建设多余的道路，所以现在从一个牲口棚到另一个牲口棚的道路是惟一的。因此，牧场运输系统可以被构建成一棵树。

John 想要知道另一次地震会造成多严重的破坏。有些道路一旦被毁坏，就会使一棵含有 PP 个牲口棚的子树和剩余的牲口棚分离，John 想知道这些道路的最小数目。

设 f(i,j)f(i,j) 代表以 ii 为根，保留 jj 个点拆掉的最小边数，而且 ii 必须保留。

初始时 f(x,1)f(x,1) 等于 xx 点的度数，转移的时候按照树形背包的方式转移：

f(x,i)=min⁡j=0i−1{f(x,i−j)+f(y,j)−2}f(x,i)=\min_{j=0}^{i-1}\{f(x,i-j)+f(y,j)-2\}

为什么是减 22 呢？因为 xx 和 yy 要连边，那么这条边就不用拆了。显然，这条边之前在 x,yx,y 各被拆了一次，所以减去 22。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int n, p, f[155][155]; // i 为根，保留 j 个点拆掉的最小边数
int siz[155];
vector <int> G[155];

void dp(int x, int fa) {
    siz[x] = 1; f[x][1] = G[x].size();
    for (int y : G[x])
        if (y != fa) {
            dp(y, x);
            siz[x] += siz[y];
            for (int i = siz[x]; i >= 0; --i) {
                for (int j = i - 1; j >= 0; --j)
                    f[x][i] = min(f[x][i], f[x][i - j] + f[y][j] - 2);
            }
        }
}

int main(void) {
    scanf("%d%d", &n, &p);
    for (int i = 1; i < n; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        G[u].emplace_back(v);
        G[v].emplace_back(u);
    }
    memset(f, 0x3f, sizeof(f));
    dp(1, 0);
    int ans = f[1][p];
    for (int i = 2; i <= n; ++i)
        ans = min(ans, f[i][p]);
    printf("%d\n", ans);
    return 0;
}

[HAOI2015] 树上染色

Portal.

有一棵点数为 n(1≤n≤2×103)n(1\le n \le 2\times 10^3) 的树，树边有边权。给你一个在 0∼n0 \sim n 之内的正整数 kk ，你要在这棵树中选择 kk 个点，将其染成黑色，并将其他 的 n−kn-k 个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间的距离的和的收益。问受益最大值是多少。

考虑每一条边的贡献，这样就可以统计了出一条边被经过了多少次。假设这条边连接的子树中有 kk 个黑色点，那么经过次数就是 k×(m−k)+(siz[y]−k)×(n−m−siz[y]+k)k\times (m-k)+(siz[y]-k)\times(n-m-siz[y]+k)，然后 kk 只能选择一个，这就是分组背包！

那么设 f[x][k]f[x][k] 代表以 xx 为根，选择了 kk 个子节点染成黑色的最大贡献。实现时有一个细节：应该把所有 ff 都初始化为 −1-1，代表是不合法的。然后令 k=0,1k=0,1 时 f=0f=0，因为只选 0,10,1 个黑点肯定合法。转移的时候倒序枚举，如果儿子的值是合法的就用树形背包的方式更新。特别的，与普通树形背包不一样，kk 的选择一定是要选 00 再选其它的，因为本来就要算上儿子点的全白贡献（即使一个黑点不选，也是有贡献的，体积为 00 但是价值不为 00，贡献必须计算）。所以转移的时候可以选择正序或者提前处理好。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;

struct edge {
	int v, d;
};

int n, m, siz[2005];
i64 f[2005][2005];
vector<edge> G[2005];

void dp(int x, int fa) 
{
	siz[x] = 1; f[x][0] = f[x][1] = 0;
	for (int i = 0; i < G[x].size(); ++i) {
		int y = G[x][i].v; i64 w = G[x][i].d;
		if (y != fa) {
			dp(y, x); siz[x] += siz[y];
			for (int j = min(m, siz[x]); j >= 0; --j) {
				if (f[x][j] != -1) f[x][j] += f[y][0] + w * siz[y] * (n - m - siz[y]);
				for (int k = min(j, siz[y]); k >= 1; --k) {
					if (f[x][j - k] == -1) continue;
					i64 val = 1ll * k * (m - k) + 1ll * (siz[y] - k) * (n - m - (siz[y] - k));
					f[x][j] = max(f[x][j], f[x][j - k] + f[y][k] + val * w);
				}
			}
		}
	}
}
                
int main(void)
{
	memset(f, -1, sizeof(f));
	scanf("%d%d", &n, &m);
	for (int i = 1; i < n; ++i) {
		int u, v, d;
		scanf("%d%d%d", &u, &v, &d);
		G[u].push_back({v, d});
		G[v].push_back({u, d});
	}
	dp(1, 0);
	printf("%lld\n", f[1][m]);
	return 0;
}

换根 DP

同样，也不是很难。

[POI2008] STA-Station

Portal.

换根 DP 的模板题。在换根的时候，我们需要知道子树大小和父亲 xx 的答案，那么儿子 yy 的答案相比父亲来讲，它所有的子树深度都减去 11，而不是它子树的深度都加上了 11。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;

int n;
int s[1000005], dep[1000005];
i64 f[1000005];
vector <int> G[1000005];
inline void addedge(int u, int v) {
    G[u].push_back(v); 
}

void dfs(int x, int fa) {
    dep[x] = dep[fa] + 1, s[x] = 1;
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i];
        if (y != fa) dfs(y, x), s[x] += s[y];
    }
}

void dp(int x, int fa) {
    for (int i = 0; i < G[x].size(); ++i) {
        int y = G[x][i];
        if (y != fa) {
            f[y] = f[x] - s[y] + (n - s[y]); // -s[y], +(n - s[y])
            dp(y, x);
        }
    }
}

int main(void) {
    scanf("%d", &n);
    for (int i = 1, u, v; i < n; ++i) {
        scanf("%d%d", &u, &v);
        addedge(u, v);
        addedge(v, u);
    }
    dfs(1, 0);
    for (int i = 1; i <= n; ++i) f[1] += dep[i];
    dp(1, 0);
    i64 ans = 0;
    int id = 0;
    for (int i = 1; i <= n; ++i)
        if (f[i] > ans) ans = f[i], id = i;
    printf("%d\n", id);
    return 0;
}

DAG 上的 DP

按照拓扑序转移。

[CF721C] The Journey

Portal.

设 f(i,j)f(i,j) 代表在 ii 走过 jj 个点的最短距离即可。

查看代码 
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <cstring>

using namespace std;
const int INF = 0x3f3f3f3f;

int n, m, k, ans, in[5005];
int f[5005][5005];
int pre[5005][5005];
vector<pair<int, int>> G[5005]; 

void Kahn(void) {
    queue<int> q;
    memset(f, 0x3f, sizeof(f));
    for (int i = 1; i <= n; ++i) if (in[i] == 0) q.push(i);
    f[1][1] = 0;
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (int i = 0; i < G[u].size(); ++i) {
            int v = G[u][i].first, w = G[u][i].second;
            for (int j = 1; j <= n; ++j) {
                if (f[v][j + 1] > f[u][j] + w) {
                    f[v][j + 1] = f[u][j] + w;
                    pre[v][j + 1] = u;
                }
                if (f[n][j] <= k) ans = max(ans, j);
            }
            --in[v]; if (in[v] == 0) q.push(v);
        }
    }
}
int p[5005];
void dfs(int x, int t) {
    p[t] = x;
    if (t > 1) dfs(pre[x][t], t - 1);
}

int main(void) {
    scanf("%d%d%d", &n, &m, &k);
    while (m--) {
        int u, v, d; scanf("%d%d%d", &u, &v, &d);
        G[u].emplace_back(make_pair(v, d)); ++in[v];
    }
    Kahn();
    printf("%d\n", ans);
    dfs(n, ans);
    for (int i = 1; i <= ans; ++i) printf("%d ", p[i]);
    putchar('\n');
    return 0;
}

杂题

补充一些题目。

[CF274B] Zero Tree

Portal.

每次必须操作 11 节点的条件过于奇怪，设 f(x),g(x)f(x),g(x) 分别代表这个节点应该加减多少，然后需要取子树中的最大值。

查看代码 
#include <bits/stdc++.h>
using namespace std; 
typedef long long i64; 

int n, a[100005]; 
vector<int> G[100005]; 
i64 f[100005], g[100005]; // f[x] 加，g[x] 减

void dfs(int x, int fa) {
    for (int y : G[x]) if (y != fa) {
        dfs(y, x); 
        f[x] = max(f[x], f[y]); 
        g[x] = max(g[x], g[y]); 
    }
    int k = a[x] + f[x] - g[x]; 
    if (k > 0) g[x] += k; 
    else f[x] -= k; 
}

int main(void) {
    ios::sync_with_stdio(0); 
    cin >> n; 
    for (int i = 1; i < n; ++i) {
        int u, v; cin >> u >> v;
        G[u].emplace_back(v); G[v].emplace_back(u); 
    }
    for (int i = 1; i <= n; ++i) cin >> a[i]; 
    dfs(1, 0); 
    cout << f[1] + g[1] << "\n"; 
    return 0; 
}
复杂结构上的 DP 问题
https://james1badcreeper.github.io/c2587cc4/
本文作者
james1BadCreeper
发布于
2022年11月5日
更新于
2023年10月30日
许可协议
CC BY-NC-SA 4.0
署名-非商业性使用-相同方式共享 4.0 国际。

发布于 2022年11月5日
算法竞赛学习笔记动态规划

动态规划

树形 DP

图上 DP

评论

若无法加载，请尝试刷新，欢迎讨论、交流和提出意见，支持 Markdown 与 LaTeX 语法（公式与文字间必须有空格）！