并查集

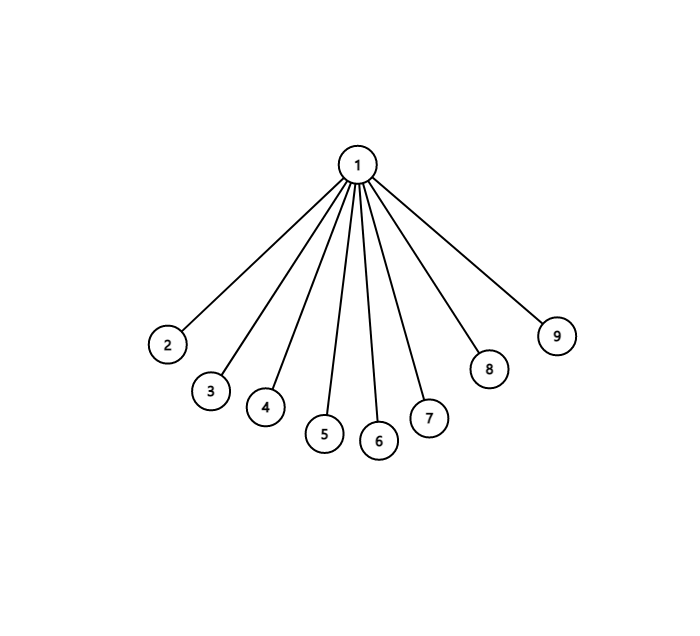
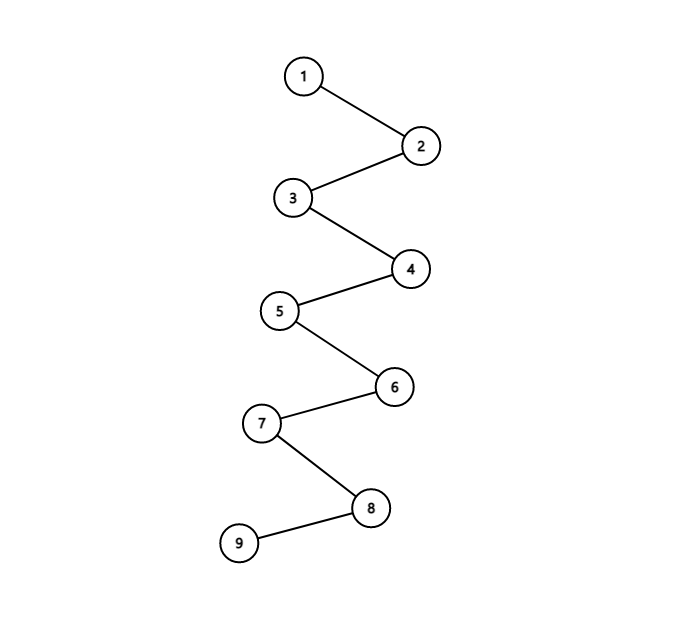
并查集（UnionFind-Set 或 Disjoint-Set）是一种可以动态维护若干个不重叠的集合的数据结构，支持合并和查询两个操作。本文将引导你学习并查集，并查集的路径压缩和按秩合并优化，以及一种特殊的并查集——带权并查集，和用并查集解决图连通性问题。

并查集维护的是 $n$ 个点的集合。正常的并查集有两种操作：

合并（Merge），将两个点所在的集合合并。
查询（Find），查询一个点属于哪个集合。

模板。

我们首先需要定义集合的表示方法。我们为每一个点分配一个数值，代表它所属的集合的编号。但这样做不行，在合并时会修改大量点的编号。正确的方法是这样的：使用森林结构，每棵树代表一个集合，树根是集合代表的元素。于是我们用 fa[x] 记录 $x$ 的父亲节点。

如果父亲节点是自己则代表它是这个集合的根节点，初始化时赋值 fa[x] = x，现在我们来看操作如何实现，比如这样一个并查集：

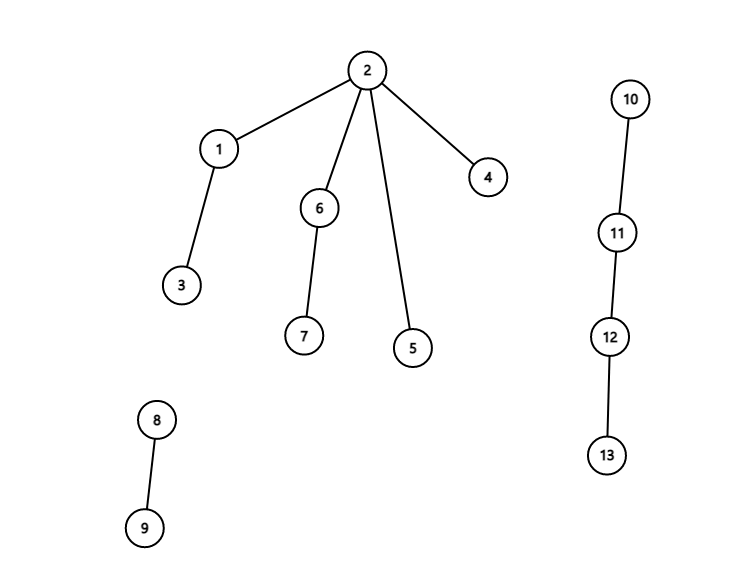
一个并查集

现在我们要查询 $7$ 所在的集合。它的父亲是 $6$ ，不是根节点，再找到 $2$ ，是根节点，返回 $2$ ，代码如下：

// 查询 x 所在的集合
int find(int x)
{
    if (fa[x] == x) return x; // 是根节点，直接返回
    return find(fa[x]); // 不是根节点，查询父亲
}

现在来看合并如何实现。比如我们要把 $9$ 所在的集合合并到 $3$ 所在的集合，我们直接把 $9$ 的根节点设置成 $3$ 的集合编号即可，像这样：

合并之后

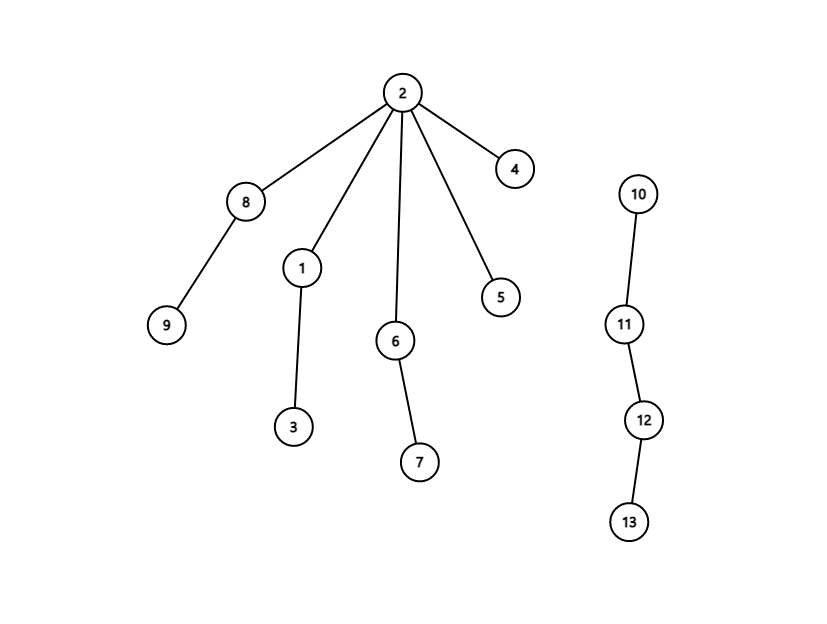
代码如下：

inline void uni(int x, int y) // 将 x 合并到 y
{
    fa[find(x)] = find(y);
}

以下代码可以通过刚才的模板：

查看代码

#include <iostream>
#include <cstdio>

using namespace std;

inline int read(void) {
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

class UnionFind_Set {
    private:
        int fa[10005];
    public:
        inline void init(int n) {
            for (int i = 1; i <= n; ++i)
                fa[i] = i;
        }
        int find(int x) {
            if (fa[x] == x) return x;
            return find(fa[x]);
        }
        inline void uni(int x, int y) {
            fa[find(x)] = find(y);
        }
        inline bool ask(int x, int y) {
            if (find(x) == find(y)) return 1;
            else return 0;
        }
}U;

int main(void) {
    int n = read(), m = read(), p = read();
    U.init(n);
    while (m--) U.uni(read(), read());
    while (p--) puts(U.ask(read(), read()) ? "Yes" : "No");
    return 0;
}

并查集的优化

实际上上述做法是很慢的，比如还是这张图：

如果我要查 13，那么它就会递归三次。万一有 $10^5$ 个数组成的链，怎么办？

看似很棘手的问题，实际上能通过很简单的方法解决。模板。

路径压缩

解决这个问题的第一种方式是路径压缩，也是竞赛中最常用的做法：因为它的代码量极小，只比刚才多了六个可见字符！

怎么做呢？由于只要在同一集合的元素在同一棵树里，那么树的形态是无所谓的，比如以下两棵树：

方便查询

查询困难

它们的意义是相同的，而且第一种查询极快。那我们只需要在查询时将查询的点直接指向它的树根就好。只需做如下代码更改：

int find(int x)
{
    if (fa[x] == x) return x;
    return fa[x] = find(fa[x]);
}

可以证明，采用路径压缩的并查集，每次 find 操作的均摊复杂度都是 $\mathcal{O}(\log n)$ 。

按秩合并

按秩合并的根本思路是在合并时就减小树的深度，这样使得树的深度本身就减小，从而降低查询的代价。

按秩合并有两种不同的方法。具体取决于秩的定义。秩可定义为树的深度（未路径压缩时）。定义 int rank[MAXN]; /* 初始化为 1，表示子树大小 */。这种方法通常比启发式合并快，代码如下：

inline void uni(int x, int y) {
    int xx = find(x), yy = find(y);
    if (xx == yy) return;
    if (rank[xx] > rank[yy]) fa[yy] = xx; // 指向大的
    else fa[xx] = yy;
    if (rank[xx] == rank[yy]) ++rank[yy]; // 相同，父亲 +1
}

另一种，当秩定义为集合的大小时，我们每次都会把小的集合合并到大的集合当中，只会增加小集合的查询代价。这样的合并方式称之为启发式合并，在许多数据结构中都能见到它的身影。

开始的时候要这样定义：int size[MAXN]; /* 将 size 数组（表示子树大小）填充为 1 */。然后这样合并：

inline void uni(int x, int y) {
    int xx = find(x), yy = find(y);
    if (xx == yy) return;
    if (size[xx] > size[yy]) swap(xx, yy); // 小的合并到大的
    fa[xx] = yy;
    size[yy] += size[xx];
}

可以证明，采用按秩合并的并查集，平均每次操作的时间复杂度也是 $\mathcal{O}(\log n)$ 。

当两种优化同时采用时，时间复杂度会降至反阿克曼函数级别。具体的资料可以自行搜索。要知道阿克曼函数的增长速度要比指数函数还要可怕，那么反阿克曼函数的增长速度也就慢的吓人，可以看作近似常数。

我们不需要但心路径压缩会对 size 或 rank 数组造成破坏，这并不会影响我们工作。

如果只采用按秩合并，那么并查集就可以实现可怕的功能：支持撤销操作，只需要把之前连上的边再指向自己即可。

并查集的复杂度

可以阅读下面这篇文章。来自 https://oi-wiki.org/ds/dsu-complexity/，根据 CC BY-SA 4.0 和 SATA 协议引用。

查看文章

这里还是说实际应用时怎么办。一般情况下我们采用路径压缩即可，但如果时间特别吃紧，则使用路径压缩加按秩合并。

但某些时候路径压缩不起作用，因为单次合并可能会造成大量修改。这时我们只使用启发式合并，而不使用路径压缩。比如可持久化并查集，线段树分治等。

这里我们采用 Loj 的并查集模板题目 Loj 109，来检验各种方法的速度。开启 O2 优化。

方法	时间	空间
暴力	TLE	15.7 M
路径压缩	690 ms	15.7 M
按秩合并	605 ms	31.0 M
路径压缩 + 按秩合并	579 ms	31.1 M
启发式合并	590 ms	31.0 M
路径压缩 + 启发式合并	601 ms	30.9 M

可以看到路径压缩的副作用还是较大的，要比按秩合并慢。但是同时采用两种优化并不会使代码快多少，所以一般使用路径压缩即可，但不意味着可以不学按秩合并——特殊情况下它能解决比路径压缩更多的问题。这里给出最后一种方法的代码参考：

查看代码

#include <iostream>
#include <cstdio>

using namespace std;
using i64 = long long;
const i64 MOD = 998244353;

inline int read(void)
{
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

class UnionFind_Set
{
    private:
        int fa[4000005], size[4000005];
    public:
        inline void init(int n)
        {
            for (int i = 1; i <= n; ++i)
                fa[i] = i, size[i] = 1;
        }
        int find(int x)
        {
            if (fa[x] == x) return x;
            return fa[x] = find(fa[x]);
        }
        inline void uni(int x, int y)
        {
            int xx = find(x), yy = find(y);
            if (xx == yy) return;
            if (size[xx] > size[yy]) swap(xx, yy);
            fa[xx] = yy;
            size[yy] += size[xx];
        }
        inline bool ask(int x, int y)
        {
            if (find(x) == find(y)) return 1;
            else return 0;
        }
}U;

int main(void)
{
    int n = read(), m = read();
    i64 ans = 0;
    U.init(n);
    while (m--)
    {
        int op = read(), x = read(), y = read();
        if (op == 0) U.uni(x, y);
        else
        {
            ans <<= 1;
            ans += U.ask(x, y);
            ans %= MOD;
        }
    }
    printf("%lld\n", ans);
    return 0;
}

并查集 Tricks

实际上并查集非常的强大。

边带权

实际上并查集是一个森林，可以拥有点权和边权。在按秩合并中，并查集就有了点权。而只要在合并的时候更新边权，那么并查集就可以统计边上的信息了。

扩展域

将一个点拆成几个点代表不同的信息，来代表具有不同性质的 $x$ 的信息。

Problemset

并查集有很多有趣的题目。

简单并查集

就是并查集。

[NOI2015] 程序自动分析

Portal.

并查集擅长维护具有传递性的条件。相等关系就有这种性质，它们在同一个集合中。而不等关系不可以用并查集维护。那么我们可以先考虑相等关系，再看不等关系是否和它们矛盾。注意到数据编号很大，需要离散化。代码如下：

查看代码

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

inline int read(void)
{
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int n, tot, m;
int a[1000005], b[1000005], type[1000005];
int d[2000005], fa[2000005];

int P(int x)
{
    return lower_bound(d + 1, d + m + 1, x) - d;
}

int find(int x)
{
    if (fa[x] == x) return x;
    return fa[x] = find(fa[x]);
}

int main(void)
{
    int T = read();
    while (T--)
    {
        n = read(), tot = 0;
        for (int i = 1; i <= n; ++i)
        {
            a[i] = read(), b[i] = read(), type[i] = read();
            d[++tot] = a[i], d[++tot] = b[i];
        }
        sort(d + 1, d + tot + 1);
        m = unique(d + 1, d + tot + 1) - (d + 1);
        for (int i = 1; i <= m; ++i) fa[i] = i;
        for (int i = 1; i <= n; ++i)
            if (type[i]) fa[find(P(a[i]))] = find(P(b[i]));
        bool flag = true;
        for (int i = 1; i <= n; ++i)
            if (!type[i] && find(P(a[i])) == find(P(b[i])))
            {
                flag = false;
                break;
            }
        puts(flag ? "YES" : "NO");
    }
    return 0;
}

[NOIP2010 提高组] 关押罪犯

Portal.

将关系按照怨气值由大到小排序，如果两个罪犯不一个集合，那么如果没有敌人则标记敌人，否则将新的敌人与原来敌人所在的集合合并。这样如果找到了两个人在一个集合内，也就是之前 $b,c$ 都是 $a$ 的敌人，那么只能让 $(a,b),(a,c)$ 不发生冲突， $(b,c)$ 发生冲突。

查看代码

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

struct Node {
    int a, b, c;
    bool operator < (const Node &a) const {
        return c > a.c;
    }
} a[100005];

int n, m, b[20005]; 
int fa[20005];

int find(int x) {
    if (fa[x] == x) return x;
    return fa[x] = find(fa[x]);
}

int main(void)
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) fa[i] = i;
    for (int i = 1; i <= m; ++i) scanf("%d%d%d", &a[i].a, &a[i].b, &a[i].c);
    sort(a + 1, a + m + 1);
    for (int i = 1; i <= m; ++i) {
        int x = find(a[i].a), y = find(a[i].b);
        if (x == y) return printf("%d\n", a[i].c), 0;
        if (!b[a[i].a]) b[a[i].a] = a[i].b;
        else fa[find(b[a[i].a])] = y;
        if (!b[a[i].b]) b[a[i].b] = a[i].a;
        else fa[find(b[a[i].b])] = x;
    }
    puts("0");
    return 0;
}

接下来我们会通过几道题目来认识带权并查集。带权并查集有很多种，要具体情况具体分析。

[NOIP2015 提高组] 信息传递

题面。

求有向图的最小环。

假说信息由 A 传递给 B，那么就连一条由 A 指向 B 的边。在连之前判断是否在一个集合里，如果在，就说明出现了环。而我们还想要知道长度，所以需要记录 d[x] 表示到父亲节点的边权。代码如下：

#include <iostream>
#include <cstdio>

using namespace std;

inline int read(void) {
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int n, ans = 0x7fffffff;
int fa[200005], d[200005];

int find(int x)
{
    if (x == fa[x]) return x; // 是自己直接返回
    int root = find(fa[x]); // 找所在集合
    d[x] += d[fa[x]]; // 为路径压缩做准备，距离设为接到父亲上
    return fa[x] = root; // 路径压缩
}

inline void uni(int x, int y)
{
    int xx = find(x), yy = find(y); // 这里的查找还有一个作用：把之前没更新的都更新，所以不用担心合并两棵树时字节点没有更新导致结果错误，就是所谓的“延迟（懒惰）更新”
    if (xx != yy) 
    {
        fa[xx] = yy; // x 的父亲为 y
        d[x] = d[y] + 1; // x 的距离为 y 到根节点的距离 +1（因为 y 是 x 的父亲）
    }
    else ans = min(ans, d[x] + d[y] + 1); // 在同一棵树里，环长度为各自到根节点的距离和 +1
}

int main(void)
{
    n = read();
    for (int i = 1; i <= n; ++i)
        fa[i] = i;
    for (int i = 1; i <= n; ++i)
        uni(i, read()); // 这是广义的合并，环是不能合并的
    printf("%d\n", ans);
    return 0;
}

这就是所谓的“边带权”并查集。每个节点到树根都有一些信息。可以发现边带权并查集依赖于路径压缩，没有路径压缩它无法正常工作（想一想，为什么）。

最小环是图论中的一个经典问题，并查集并不能解决它的所有变种。请学有余力读者自行寻找 dfs、Tarjan、Floyd 等资料。

[NOI2002] 银河英雄传说

题面。

由于距离的存在，很容易想到用边带权并查集来解决。由于合并时的特殊性，我们还需要记录集合的大小。

查看代码

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

inline int read(void)
{
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int fa[30005];
int d[30005], Size[30005];

int find(int x)
{
    if (fa[x] == x) return x;
    int root = find(fa[x]);
    d[x] += d[fa[x]];
    return fa[x] = root;
}

inline void uni(int x, int y)
{
    int xx = find(x), yy = find(y);
    fa[xx] = yy, d[xx] = Size[yy];
    Size[yy] += Size[xx];
}

int main(void)
{
    int T = read();
    for (int i = 1; i <= 30000; ++i)
        fa[i] = i, Size[i] = 1;
    while (T--)
    {
        char s[3];
        int i, j;
        scanf("%s%d%d", s, &i, &j);
        if (s[0] == 'C')
        {
            if (find(i) == find(j)) printf("%d\n", abs(d[i] - d[j]) - 1);
            else puts("-1");
        }
        else uni(i, j);
    }
    return 0;
}