抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

块状数据结构

更新于 2023年3月1日

13.6k 字

73 分钟

次浏览

本文正在施工中，有缺失的内容请谅解。

分块（又称根号算法，因为单次操作复杂度是根号级别），是一种重要的思想，可以用来解决较为简单的题目，也可以用来解决各种可怕的问题。尽管如此，分块的思想不难理解。

大家在数据结构中应该都听说过分块，因为嵌套数据结构、分块数据结构和可持久化数据结构背称为数据结构三大毒瘤重要思想。但实际上，除了在数据结构中的应用，分块在其它方面也有许多应用。

分块基础

分块的基本思想是，通过对原数据的适当划分，并在划分后的每一个块上预处理部分信息，从而较一般的暴力算法取得更优的时间复杂度。

这么说很空虚，我们通过几道入门题来一一看一下分块的简单应用。

数列分块入门

这是 Loj 上的一个系列题。但是前两个都比较简单，所以这里不写了，大家可以学习完之后写一下练习练习，我们先做一下最为经典的 3。

Portal.

啊，我知道你会树状数组和线段树，我们今天要用分块以龟速解决这道题。

我们把序列 AA 分成若干个长度块，如下图：

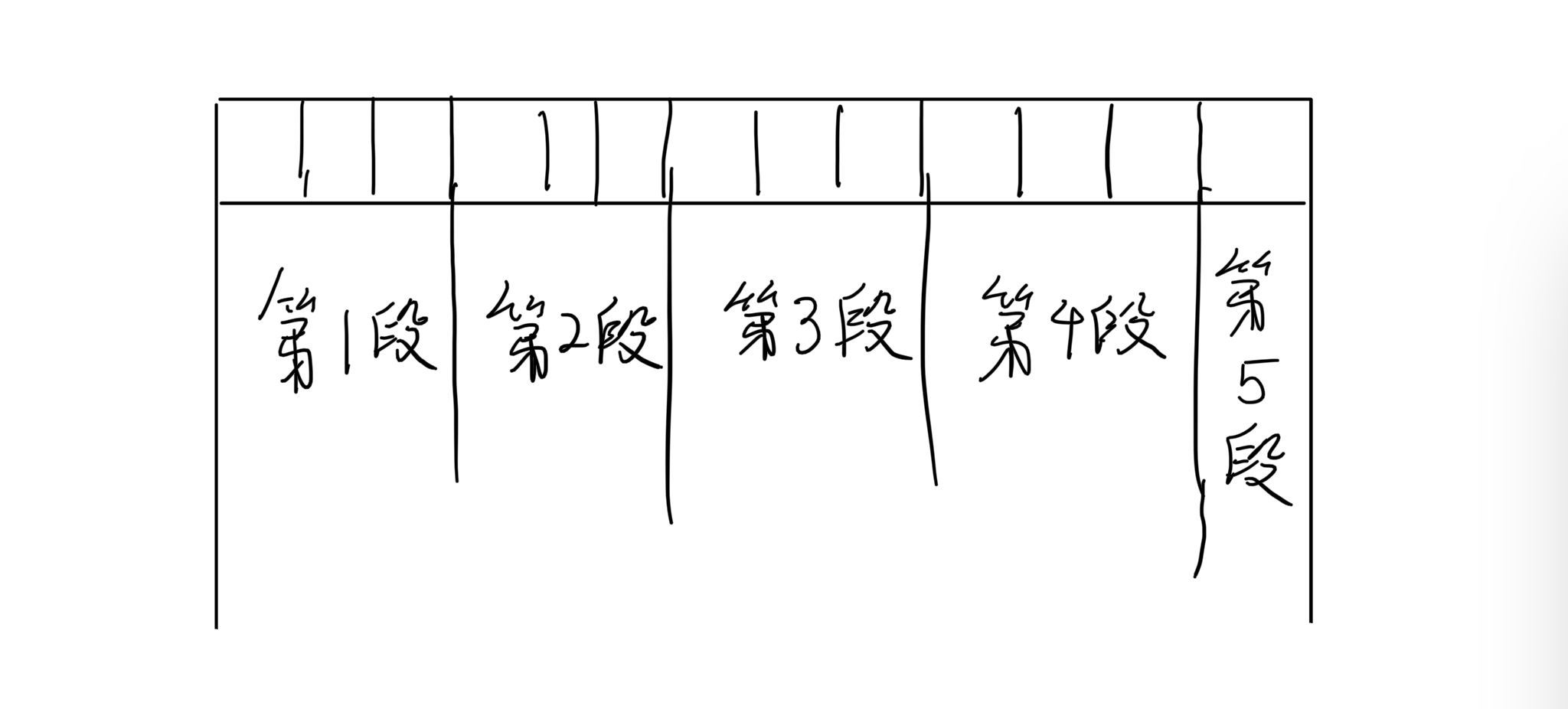
分块后的序列
分块后的序列

具体怎么分呢？把若干个数分成一块。我们记录每个点的数值，再记录每个块的和（记作 sum[i]sum[i]），还要给每个块打上一个标记 add[i]add[i]（类似于线段树的延迟标记，而且标记是永久的，否则你往哪传）。

在进行操作的时候，我们把连续的块称之为整块，两边的不完整的块称为零散块。

对于修改操作，分两种情况进行：

  • 当 xx 和 yy 处于同一段时，直接暴力加，然后令这一段 sum[i]+=k×(y−x+1)sum[i]+=k\times(y-x+1)；
  • 否则，设 xx 处于第 pp 段，rr 处于第 qq 段。对于 i∈[p+1,q−1]i\in [p+1,q-1]，令 add[i]+=kadd[i]+=k。对于开头、结尾不足一整段的两部分，按照前一种情况暴力更新。

对于查询操作，也分两种情况：

  • 当 xx 和 yy 处于同一段时，∑i=xy+add[i]×(y−x+1)\sum\limits_{i=x}^{y}+add[i]\times (y-x+1) 就是答案。
  • 否则，设 xx 处于第 pp 段，rr 处于第 qq 段。记 ans=0ans=0。对于 i∈[p+1,q−1]i\in [p+1,q-1]，令 ans+=sum[i]+add[i]×len[i]ans+=sum[i]+add[i]\times len[i]，lenlen 表示这一段的长度。对于开头、结尾不足一整段的两部分，按照前一种情况暴力查询。

当块的长度较长时，操作的暴力会比较慢（全堆在一个块里）；块的长度较短时，维护部分会比较慢（块变多了，改的 addadd 标记数量变多了）。

根据经验，当块的大小在序列长度的算术平方根时会比较快，证明可以采用均值不等式，设块的大小为 tt：

t+nt≥2t×nt=2nt+\frac{n}{t}\ge 2\sqrt{t\times\frac{n}{t}} = 2\sqrt{n}

当且仅当 t=nt  ⟺  t2=nt=\frac{n}{t}\iff t^2=n 时等号成立。

然而在某些毒瘤题中，还可能需要通过实验确定最好的块值（我们接下来会看到的）。

接下来就到了愉快的写代码时间，基本结构是这样：

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;
using i64 = long long;

inline int read(void) {
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int n, m, t;
i64 a[100005], sum[100005], add[100005]; // 原序列，块和，延迟标记
int pos[100005], L[100005], R[100005]; // 元素所在额块的编号，块的左右端点

inline void update(int l, int r, i64 k) {
    // do update
}

inline i64 query(int l, int r) {
    // do query
}

int main(void) {
    n = read(), m = read();
    t = sqrt(n); // 分块
    for (int i = 1; i <= n; ++i) a[i] = read();
    for (int i = 1; i <= t; ++i) // 先处理好这 t 个块的左右端点
    {
        L[i] = (i - 1) * t + 1;
        R[i] = i * t;
    }
    if (R[t] < n) ++t, L[t] = R[t - 1] + 1, R[t] = n; // 最后剩一小段不够凑成完整的块
    //========== 预处理 ========== start >
    for (int i = 1; i <= t; ++i)
        for (int j = L[i]; j <= R[i]; ++j)
        {
            pos[j] = i;
            sum[i] += a[j];
        }
    //========== 预处理 ========== end >
    while (m--)
    {
        int op = read(), x = read(), y = read();
        if (op == 1) update(x, y, read());
        else printf("%lld\n", query(x, y));
    }
    return 0;
}

实际上 sum, L, R 数组无需开这么大，但已经没有优化的必要了。

两个操作的代码如下：

void update(int l, int r, i64 k) {
    int p = pos[l], q = pos[r];
    if (p == q) // 同个块内，暴力
    {
        for (int i = l; i <= r; ++i) a[i] += k;
        sum[p] += (r - l + 1) * k;
        return;
    }
    for (int i = p + 1; i < q; ++i) add[i] += k; // 大块打标记
    for (int i = l; i <= R[p]; ++i) a[i] += k; // 左
    sum[p] += (R[p] - l + 1) * k; // 和
    for (int i = L[q]; i <= r; ++i) a[i] += k; // 右
    sum[q] += (r - L[q] + 1) * k; // 和
}

i64 query(int l, int r)
{
    // 同 update
    int p = pos[l], q = pos[r];
    i64 ans = 0;
    if (p == q)
    {
        for (int i = l; i <= r; ++i) ans += a[i];
        ans += add[p] * (r - l + 1);
        return ans;
    }
    for (int i = p + 1; i < q; ++i) ans += sum[i] + add[i] * (R[i] - L[i] + 1);
    for (int i = l; i <= R[p]; ++i) ans += a[i];
    ans += add[p] * (R[p] - l + 1);
    for (int i = L[q]; i <= r; ++i) ans += a[i];
    ans += add[q] * (r - L[q] + 1);
    return ans;
}

时间复杂度为 O(mn)\mathcal{O}(m\sqrt{n})。

上述做法还可以优化，不过时间复杂度并没有变。

优化的方式是前缀和，大体思路是明确的。然而在有修改的情况下，前缀和不方便维护，只能维护单个块内的前缀和，这样零散块的查询就可以使用前缀和了。

复杂度分析

分块的复杂度要从查询和修改，整块和零散块来看。比如刚才的题，若将序列分为 tt 块：

  • 查询：
    • 整块 O(t)O(t)，
    • 零散块 O(nt)O(\frac{n}{t})，
  • 修改
    • 整块 O(t)O(t)，
    • 零散块 O(nt)O(\frac{n}{t})。

块状数组

刚才的分块是针对数组的，这类分块我们统称为块状数组。接下来我们将见识更多的题目来详细认识块状数组。

基础训练

这些题都很基础。

[Luogu P2801] 教主的魔法

Portal.

区间加，查询区间大于等于某个数的数的个数。

树状数组维护的是前缀和，线段树维护的信息满足大区间的解可以由小区间合并得到（区间可加性）。但是很可惜，这么奇怪的查询内容虽然满足区间可加性，但是每一个不同的 c 值需要有不同的线段树，所以结论就是用普通线段树做就是送猪头。

但是树套树是可以维护这种复杂信息的，然而树套树做不到区间修改，所以使用分块来解决。

分块之后，我们看一看要怎么查询。我们将每一个块作为一个子问题分别求解。先将这个块排好序，那么查询时就能快很多（直接二分）。什么时候排序？显然是修改的时候，而且只有暴力修改的部分（因为只有它的顺序会变化）。代码如下：

查看代码 
#include <bits/stdc++.h>
using namespace std;

inline int read(void) {
    int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) x = (x<<3) + (x<<1) + (c^48), c = getchar();
    return x;
}

int n, q, t;
int L[1000005], R[1000005], pos[1000005];
int a[1000005], T[1000005], add[1000005];

inline void calc(int p) {
    for (int i = L[p]; i <= R[p]; ++i) T[i] = a[i];
    sort(T + L[p], T + R[p] + 1);
}

inline void update(int l, int r, int k) {
    int p = pos[l], q = pos[r];
    if (p == q) {
        for (int i = l; i <= r; ++i) a[i] += k;
        return calc(p);
    }
    for (int i = l; i <= R[p]; ++i) a[i] += k;
    for (int i = L[q]; i <= r; ++i) a[i] += k;
    for (int i = p + 1; i < q; ++i) add[i] += k;
    calc(p), calc(q);
}

inline int answer(int l, int r, int c) {
    int ans = 0, p = pos[l], q = pos[r];
    if (p == q) {
        for (int i = l; i <= r; ++i) if (a[i] + add[p] >= c) ++ans;
        return ans;
    }
    for (int i = l; i <= R[p]; ++i) if (a[i] + add[p] >= c) ++ans;
    for (int i = L[q]; i <= r; ++i) if (a[i] + add[q] >= c) ++ans;
    for (int i = p + 1; i < q; ++i)
        ans += R[i] - (lower_bound(T + L[i], T + R[i] + 1, c - add[i]) - T) + 1;
    return ans;
}

int main(void) {
    n = read(), q = read(); t = sqrt(n);
    for (int i = 1; i <= n; ++i) a[i] = read();
    for (int i = 1; i <= t; ++i) L[i] = (i - 1) * t + 1, R[i] = i * t; 
    if (R[t] < n) R[++t] = n, L[t] = R[t - 1] + 1;
    for (int i = 1; i <= t; ++i) {
        for (int j = L[i]; j <= R[i]; ++j) pos[j] = i;
        calc(i);
    }
    while (q--) {
        char op[3];
        scanf("%s", op);
        if (op[0] == 'M') {
            int l = read(), r = read(), k = read();
            update(l, r, k);
        } else {
            int l = read(), r = read(), c = read();
            printf("%d\n", answer(l, r, c));
        }
    }
    return 0;
}

我们设把原序列分成 xx 个块，那么查询的时候：

  • 整块 O(xlog⁡nx)O\left(x\log \cfrac{n}{x}\right)，
  • 零散块 O(nx)O\left(\cfrac{n}{x}\right)。

修改复杂度：

  • 整块 O(1)O(1)，
  • 零散块 O(nx)O\left(\cfrac{n}{x}\right)。

当块的大小为 nlog⁡n\sqrt{n\log n} 的时候，时间复杂度可以达到利用这种做法的最优的 O(mnlog⁡n)O(m\sqrt{n\log n})。

同样，你也可以通过实验来确定更好的块长。

静态分块

以强制在线的区间众数为代表。以上提到的分块都是动态分块，它们可以处理带修问题。而静态分块则不带修，通过预处理块的信息来得到复杂度较优的做法。静态分块在功能上是接下来要介绍的莫队算法的子集，而且时空常数静态分块都会更大。但是如果强制在线的话，只能使用静态分块。

[Violet] 蒲公英

Portal.

静态多次询问区间众数，强制在线。

区间众数不具有区间可加性，所以不可以使用线段树维护。

我们预处理出数组 c[x][y][num]c[x][y][num]，代表 numnum 在块 [x][y][x][y] 中的出现次数，同时预处理出答案。在查询的时候，整块的答案可以直接得到，零散块只需要单次扫描统计即可。

设块的大小为 TT，那么时间复杂度为 O(nT2+mn/T)O(nT^2+mn/T)，那么当 T=n3T=\sqrt[3]{n} 时会比较快，时间复杂度为 O(n35)O(n^{\frac{3}{5}})。这种做法比较慢，而且空间较大。

查看代码 
#include <bits/stdc++.h>
using namespace std;

int n, m, tot, ans[2];
int a[40005], b[40005];
int c[37][37][40005], f[37][37][2];
int L[205], R[205], pos[40005];

void work(int x, int y, int num) {
    ++c[x][y][num];
    if (c[x][y][num] > ans[0] || (c[x][y][num] == ans[0] && num < ans[1]))
        ans[1] = num, ans[0] = c[x][y][num];
}

int query(int l, int r) {
    int p = pos[l], q = pos[r];
    int x = 0, y = 0;
    if (p + 1 <= q - 1) x = p + 1, y = q - 1;
    memcpy(ans, f[x][y], sizeof(ans));
    if (p == q) {
        for (int i = l; i <= r; ++i) work(x, y, a[i]);
        for (int i = l; i <= r; ++i) --c[x][y][a[i]];
    } else {
        for (int i = l; i <= R[p]; ++i) work(x, y, a[i]);
        for (int i = L[q]; i <= r; ++i) work(x, y, a[i]);
        for (int i = l; i <= R[p]; ++i) --c[x][y][a[i]];
        for (int i = L[q]; i <= r; ++i) --c[x][y][a[i]];
    }
    return b[ans[1]];
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i);
    memcpy(b, a, sizeof(b));
    sort(b + 1, b + n + 1);
    tot = unique(b + 1, b + n + 1) - (b + 1);
    for (int i = 1; i <= n; ++i)
        a[i] = lower_bound(b + 1, b + tot + 1, a[i]) - b;
    
    int t = pow(double(n), (double)1 / 3);
    int len = t ? n / t : n;

    for (int i = 1; i <= t; ++i) {
        L[i] = R[i - 1] + 1; R[i] = i * len;
    }
    if (R[t] < n) { 
        L[t + 1] = R[t] + 1;
        R[++t] = n; 
    }

    for (int i = 1; i <= t; ++i)
        for (int j = L[i]; j <= R[i]; ++j)
            pos[j] = i;

    memset(c, 0, sizeof(c));
    memset(f, 0, sizeof(f));    
    for (int i = 1; i <= t; ++i)
        for (int j = i; j <= t; ++j) {
            for (int k = L[i]; k <= R[j]; ++k)
                ++c[i][j][a[k]];
            for (int k = 1; k <= tot; ++k)
                if (c[i][j][k] > f[i][j][0]) {
                    f[i][j][0] = c[i][j][k];
                    f[i][j][1] = k;
                }
        }

    int last = 0;
    while (m--) {
        int l, r;
        scanf("%d%d", &l, &r);
        l = (l + last - 1) % n + 1; r = (r + last - 1) % n + 1;
        if (l > r) swap(l, r);
        printf("%d\n", last = query(l, r));
    }
    return 0;
}

[Ynoi2019 模拟赛] Yuno loves sqrt technology III

Portal.

这次询问的是区间众数的出现次数，但本质上是一样的。我们记录 f(i,j)f(i,j) 代表第 [i,j][i,j] 块的区间众数出现次数。我们对每一个数都开一个 STL vector，记录其出现的位置，并记 ax[i]ax[i] 为第 ii 个数出现在其 vector 中的位置。

整块的答案是可以直接统计的，而对于零散块，则获取当前的数在 vector 中的位置，考虑 ansans 是否可以变大，进行暴力更新即可。由于 ansans 最多变大 2n2\sqrt{n}，因此询问的时间复杂度为 O(n)O(\sqrt{n})。

总时间复杂度为 O(nn)O(n\sqrt{n})。如果想要求出区间众数的值，额外记录一个即可。

查看代码 
#include <bits/stdc++.h>

int read(void) {
    int x = 0, c = getchar_unlocked();
    while (!isdigit(c)) c = getchar_unlocked();
    while (isdigit(c)) x = x * 10 + c - '0', c = getchar_unlocked();
    return x;
}
void print(int x) {
    if (x > 9) print(x / 10);
    putchar_unlocked(x % 10 + '0');
}

int n, m, tot;
int a[500005], b[500005], pos[500005];
int L[720], R[720], f[720][720];
int cnt[500005], ax[500005];
std::vector <int> v[500005];

int query(int l, int r) {
    int p = pos[l], q = pos[r], ans = f[p + 1][q - 1];
    if (p == q) {
        for (int i = l; i <= r; ++i) cnt[a[i]] = 0;
        for (int i = l; i <= r; ++i) ans = std::max(ans, ++cnt[a[i]]);
        return ans;
    }
    for (int i = l; i <= R[p]; ++i) {
        int p = ax[i];
        while (p + ans < v[a[i]].size() && v[a[i]][p + ans] <= r) ++ans;
    }
    for (int i = L[q]; i <= r; ++i) {
        int p = ax[i];
        while (p - ans >= 0 && v[a[i]][p - ans] >= l) ++ans;
    }
    return ans;
}

int main(void) {
    n = read(), m = read();
    for (int i = 1; i <= n; ++i) b[i] = a[i] = read();
    std::sort(b + 1, b + n + 1);
    tot = std::unique(b + 1, b + n + 1) - (b + 1);
    for (int i = 1; i <= n; ++i) {
        a[i] = std::lower_bound(b + 1, b + tot + 1, a[i]) - b;
        v[a[i]].emplace_back(i); ax[i] = v[a[i]].size() - 1;
    }

    int t = sqrt(n);
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = i * t;
    if (R[t] < n) { ++t; L[t] = R[t - 1] + 1; R[t] = n;}
    for (int i = 1; i <= t; ++i) for (int j = L[i]; j <= R[i]; ++j) pos[j] = i;
    for (int i = 1; i <= t; ++i) {
        memset(cnt, 0, sizeof(cnt));
        for (int j = i; j <= t; ++j) {
            f[i][j] = f[i][j - 1];
            for (int k = L[j]; k <= R[j]; ++k)
                f[i][j] = std::max(f[i][j], ++cnt[a[k]]);
        }
    }

    int last = 0;
    while (m--) {
        int l = (read() ^ last), r = (read() ^ last);
        print(last = query(l, r));
        putchar_unlocked('\n');
    }
    return 0;
}

[Luogu P3709] 大爷的字符串题

Portal.

可以将序列划分成若干个单调上升序列，那么问的就是区间众数出现次数的相反数。

[Ynoi2019 模拟赛] Yuno loves sqrt technology I

Portal.

强制在线的区间逆序对！

  • 整块内部：预处理；
  • 散块内部：用树状数组预处理前后缀；
  • 散块对散块：处理好每个数的排名，直接归并；
  • 散块对整块：预处理出 gi,jg_{i,j} 代表 1∼j1\sim j 对 ii 块的贡献。
查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 
const int B = 350; 

template<typename T>
inline void read(T &x) {
    x = 0; int c = getchar_unlocked(); 
    while (!isdigit(c)) c = getchar_unlocked(); 
    while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar_unlocked(); 
}

int n, m; 
int a[100005], pos[100005]; 
int b[100005], idx[100005], T[100005]; 
int L[750], R[750]; 
i64 f[750][750]; 
int g[750][100005], pre[100005], nxt[100005]; // 1 ~ j 对第 i 块的贡献
int T1[750], T2[750], t1, t2; 

struct Fenwick {
    int C[100005]; 
    inline void add(int x, int k) { for (; x <= n; x += x & -x) C[x] += k; }
    inline int sum(int x) { int r = 0; for (; x; x -= x & -x) r += C[x]; return r; }
} F;  

inline int merge(int *a, int na, int *b, int nb) {
    int res = 0;
    for (int p = 1, q = 1; p <= na && q <= nb; ) {
        if (q <= nb && (p > na || b[q] < a[p])) ++q, res += na - p + 1; 
        else ++p; 
    } 
    return res; 
}
inline i64 query(int l, int r) {
    int p = pos[l], q = pos[r]; 
    if (p == q) {
        i64 ans = pre[r] - (l == L[p] ? 0 : pre[l - 1]); t1 = 0; t2 = 0; 
        for (int i = L[p]; i <= R[p]; ++i) 
            if (idx[b[i]] >= L[p] && idx[b[i]] <= l - 1) T1[++t1] = b[i]; 
            else if (idx[b[i]] >= l && idx[b[i]] <= r) T2[++t2] = b[i]; 
        return ans - merge(T1, t1, T2, t2); 
    }
    i64 ans = f[p + 1][q - 1] + nxt[l] + pre[r]; 
    t1 = 0; t2 = 0; 
    for (int i = L[p]; i <= R[p]; ++i) if (idx[b[i]] >= l) T1[++t1] = b[i]; 
    for (int i = L[q]; i <= R[q]; ++i) if (idx[b[i]] <= r) T2[++t2] = b[i]; 
    ans += merge(T1, t1, T2, t2);  
    for (int i = p + 1; i < q; ++i) ans += g[i][R[p]] - g[i][l - 1] + g[i][r] - g[i][L[q] - 1]; 
    return ans; 
}

int main(void) {
    read(n); read(m); int t = (n - 1) / B + 1; 
    for (int i = 1; i <= n; ++i) read(a[i]), idx[a[i]] = i, T[i] = b[i] = a[i]; 
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = i * B; R[t] = n; 
    for (int i = 1; i <= t; ++i) {
        for (int j = L[i]; j <= R[i]; ++j) pos[j] = i; 
        sort(b + L[i], b + R[i] + 1);  
    }

    // 散块内部，预处理
    for (int op = 1; op <= t; ++op) {
        for (int i = L[op]; i <= R[op]; ++i) pre[i] = (i == L[op] ? 0 : pre[i - 1]) + ((i - L[op]) - F.sum(a[i] - 1)), F.add(a[i], 1); 
        for (int i = L[op]; i <= R[op]; ++i) F.add(a[i], -1); 
        for (int i = R[op]; i >= L[op]; --i) nxt[i] = (i == R[op] ? 0 : nxt[i + 1]) + F.sum(a[i] - 1), F.add(a[i], 1); 
        for (int i = R[op]; i >= L[op]; --i) F.add(a[i], -1); 
        f[op][op] = pre[R[op]]; 
    }

    // 散块对整块，整块对整块，预处理
    sort(T + 1, T + n + 1); 
    for (int op = 1; op <= t; ++op)
        for (int i = 1, k = L[op] - 1; i <= n; ++i) {
            while (k < R[op] && T[i] > b[k + 1]) ++k; 
            int p = idx[T[i]]; 
            if (p < L[op]) g[op][p] = k - L[op] + 1; 
            else if (p > R[op]) g[op][p] = R[op] - k; 
        }
    for (int op = 1; op <= t; ++op) for (int i = 1; i <= n; ++i) g[op][i] += g[op][i - 1]; 
    for (int len = 1; len < t; ++len)
        for (int i = 1; i + len <= t; ++i) {
            int j = i + len; 
            f[i][j] = f[i + 1][j] + f[i][j - 1] - f[i + 1][j - 1] + g[j][R[i]] - g[j][L[i] - 1]; 
        }

    for (i64 last = 0; m--; ) {
        i64 l, r; read(l); read(r); l ^= last, r ^= last; 
        printf("%lld\n", last = query(l, r)); 
    }
    return 0;
}

一些简单题

简单的分块题。

[Ynoi2017] 由乃打扑克

Portal.

套用《教主的魔法》的二分法，在查询的时候二分出排名为 kk 的数即可。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 200;
const int INF = 2e9 + 1e8;

inline int read(void) {
    int x = 0, c = getchar_unlocked(), f = 1;
    while (!isdigit(c)) {if (c == '-') f = -1; c = getchar_unlocked();}
    while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar_unlocked();
    return x * f;
}

int n, m, t;
int a[100005], T[100005];
int L[800], R[800], add[800], pos[100005];

inline void calc(int p) {
    for (int i = L[p]; i <= R[p]; ++i) T[i] = a[i];
    sort(T + L[p], T + R[p] + 1);
}

inline void update(int l, int r, int k) {
    int p = pos[l], q = pos[r];
    if (p == q) {
        for (int i = l; i <= r; ++i) a[i] += k;
        calc(p); return;
    }
    for (int i = p + 1; i < q; ++i) add[i] += k;
    for (int i = l; i <= R[p]; ++i) a[i] += k;
    for (int i = L[q]; i <= r; ++i) a[i] += k;
    calc(p); calc(q);
}

inline pair<int, int> get(int l, int r) {
    int p = pos[l], q = pos[r], minn = INF, maxx = -INF;
    if (p == q) {
        for (int i = l; i <= r; ++i) minn = min(minn, a[i] + add[p]), maxx = max(maxx, a[i] + add[p]);
        return make_pair(minn, maxx);
    }
    for (int i = p + 1; i < q; ++i) minn = min(minn, T[L[i]] + add[i]), maxx = max(maxx, T[R[i]] + add[i]);
    for (int i = l; i <= R[p]; ++i) minn = min(minn, a[i] + add[p]), maxx = max(maxx, a[i] + add[p]);
    for (int i = L[q]; i <= r; ++i) minn = min(minn, a[i] + add[q]), maxx = max(maxx, a[i] + add[q]);
    return make_pair(minn, maxx);
}

inline int check(int l, int r, int x) { // 询问 [l,r] 中 x 是第几小的数
    int p = pos[l], q = pos[r], cnt = 0;
    if (p == q) {
        for (int i = l; i <= r; ++i) if (a[i] + add[p] <= x) ++cnt;
        return cnt;
    }
    for (int i = l; i <= R[p]; ++i) if (a[i] + add[p] <= x) ++cnt;
    for (int i = L[q]; i <= r; ++i) if (a[i] + add[q] <= x) ++cnt;
    for (int i = p + 1; i < q; ++i) if (T[L[i]] + add[i] <= x) {
        if (T[R[i]] + add[i] <= x) cnt += R[i] - L[i] + 1;
        else cnt += upper_bound(T + L[i], T + R[i] + 1, x - add[i]) - (T + L[i]);
    }
    return cnt;
}

inline int query(int l, int r, int k) {
    if (r - l + 1 < k) return -1;
    int p = pos[l], q = pos[r]; 
    pair<int, int> t = get(l, r);
    int ll = t.first - 1, rr = t.second + 1;
    while (ll + 1 != rr) {
        int mid = ((long long)ll + rr) / 2;
        if (check(l, r, mid) < k) ll = mid;
        else rr = mid;
    }
    return rr;
}

int main(void) {
    n = read(), m = read();
    for (int i = 1; i <= n; ++i) a[i] = read();
    t = n / BLOCK_SIZE;
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = BLOCK_SIZE * i;
    R[t] = n;
    for (int i = 1; i <= t; ++i) {
        for (int j = L[i]; j <= R[i]; ++j) pos[j] = i;
        calc(i);
    }
    while (m--) {
        int op = read(), l = read(), r = read(), k = read();
        if (op == 1) printf("%d\n", query(l, r, k));
        else update(l, r, k);
    }
    return 0;
}

莫队

有时题目的查询非常诡异，常规的在线做法（读入一个询问回答一个）不起作用，需要离线做法（读入所有询问后统一处理）。如果还要对询问进行分块，那么莫队就出现了。

普通莫队

[国家集训队] 小 Z 的袜子。

nn 个不同的数，每次询问一个区间 [l,r][l,r]，问在当中有多大概率抽到两个一样的数。

常规的离线做法似乎不太行，只是将询问按照右端点排序的话，无法通过前缀和相减的方式得到区间每个种类数的个数。我们可以通过莫队解决这个问题：

将询问按照左端点排序，然后分成 n\sqrt{n} 块，每个块内再按照右端点排序。这样保证了在每个块内，询问的左端点变化范围在 n\sqrt{n} 内。这样之后我们就可以暴力移动询问区间，而且注定了移动次数为 O(nn)O(n\sqrt{n})。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;
const int BLOCK_SIZE = 250;

i64 gcd(i64 x, i64 y) {
    if (y == 0) return x;
    return gcd(y, x % y);
}

int n, m;
int a[50005], cnt[50005], pos[50005];
i64 ans, ans1[50005], ans2[50005];

struct Question {
    int l, r, id;
    bool operator < (const Question &a) {
        if (pos[l] == pos[a.l]) return r < a.r;
        return l < a.l;
    }
} Q[50005];

void update(int p, int f) {
    if (cnt[a[p]]) ans -= cnt[a[p]] * (cnt[a[p]] - 1);
    cnt[a[p]] += f;
    if (cnt[a[p]]) ans += cnt[a[p]] * (cnt[a[p]] - 1);
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i);
    for (int i = 1; i <= n; ++i) pos[i] = (i - 1) / BLOCK_SIZE + 1;
    for (int i = 1; i <= m; ++i) scanf("%d%d", &Q[i].l, &Q[i].r), Q[i].id = i;
    sort(Q + 1, Q + m + 1);
    for (int i = 1, l = 1, r = 0; i <= m; ++i) {
        for (; r + 1 <= Q[i].r; ++r) update(r + 1, 1);
        for (; r - 1 >= Q[i].r; --r) update(r, -1);
        for (; l + 1 <= Q[i].l; ++l) update(l, -1);
        for (; l - 1 >= Q[i].l; --l) update(l - 1, 1);
        if (Q[i].l == Q[i].r) {
            ans1[Q[i].id] = 0, ans2[Q[i].id] = 1;
            continue;
        }
        ans1[Q[i].id] = ans;
        ans2[Q[i].id] = 1ll * (r - l + 1) * (r - l);
    }
    for (int i = 1; i <= m; ++i) {
        if (ans1[i] == 0) ans2[i] = 1;
        else {
            int g = gcd(ans1[i], ans2[i]);
            ans1[i] /= g, ans2[i] /= g;
        }
        printf("%lld/%lld\n", ans1[i], ans2[i]);
    }
    return 0;
}

奇偶排序优化。当 ll 位于的块确定时，根据其奇偶性分别让 rr 升序 / 降序排列，通常可以快 30%30\%。

树上莫队

莫队上树！但是关键是拍到序列上。

链上维护

可以利用欧拉序将其拍到线性结构上（欧拉序在不在链上的内容会直接访问两次来消除其影响）

[COT2] Count on a tree II.

nn 个节点的带颜色树，询问路径上不同颜色的数量。

树上莫队模板，注意 LCA 处的讨论。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 300; 

int n, m, pos[80005], Ans[40005], dep[40005]; 
int a[40005], b[40005], f[16][40005]; 
int idx[80005], tot, L[80005], R[80005]; 
vector<int> G[40005]; 

struct Query {
    int l, r, lca, id; 
    bool operator< (const Query &a) const {
        if (pos[l] == pos[a.l]) return r < a.r; 
        return l < a.l; 
    }
} Q[100005];

void dfs(int x, int fa) {
    idx[L[x] = ++tot] = x; dep[x] = dep[f[0][x] = fa] + 1; 
    for (int i = 1; i <= 15; ++i) f[i][x] = f[i - 1][f[i - 1][x]]; 
    for (int y : G[x]) if (y != fa) dfs(y, x); 
    idx[R[x] = ++tot] = x; 
}
int LCA(int x, int y) {
    if (dep[x] < dep[y]) swap(x, y); 
    for (int i = 15; i >= 0; --i) if (dep[f[i][x]] >= dep[y]) x = f[i][x]; 
    if (x == y) return x; 
    for (int i = 15; i >= 0; --i) if (f[i][x] != f[i][y]) x = f[i][x], y = f[i][y];
    return f[0][x]; 
}

int ans, buc[40005]; bool vis[40005]; 
void update(int x) {
    vis[x] ^= 1; 
    if (vis[x] == 1) {
        if (buc[a[x]] == 0) ++ans; 
        ++buc[a[x]]; 
    } else {
        if (buc[a[x]] == 1) --ans;
        --buc[a[x]]; 
    }
}

int main(void) {
    scanf("%d%d", &n, &m); 
    for (int i = 1; i <= n; ++i) scanf("%d", a + i), b[i] = a[i]; 
    sort(b + 1, b + n + 1); int nn = unique(b + 1, b + n + 1) - (b + 1); 
    for (int i = 1; i <= n; ++i) a[i] = lower_bound(b + 1, b + nn + 1, a[i]) - b; 
    for (int i = 1; i < n; ++i) {
        int u, v; scanf("%d%d", &u, &v); 
        G[u].emplace_back(v); G[v].emplace_back(u); 
    } dfs(1, 0); 
    for (int i = 1; i <= tot; ++i) pos[i] = (i - 1) / BLOCK_SIZE + 1; 
    for (int i = 1; i <= m; ++i) {
        int x, y; scanf("%d%d", &x, &y); Q[i].id = i; int d = LCA(x, y); 
        if (L[x] > L[y]) swap(x, y); 
        if (x == d) Q[i].l = L[x], Q[i].r = L[y]; 
        else Q[i].l = R[x], Q[i].r = L[y], Q[i].lca = d; 
    }
    sort(Q + 1, Q + m + 1); 
    for (int i = 1, l = 1, r = 0; i <= m; ++i) {
        while (r < Q[i].r) update(idx[++r]); 
        while (r > Q[i].r) update(idx[r--]); 
        while (l > Q[i].l) update(idx[--l]); 
        while (l < Q[i].l) update(idx[l++]); 
        if (Q[i].lca) update(Q[i].lca); 
        Ans[Q[i].id] = ans; 
        if (Q[i].lca) update(Q[i].lca); 
    }
    for (int i = 1; i <= m; ++i) printf("%d\n", Ans[i]); 
    return 0;
}

子树维护

虽然可以使用 DFS 序拍到链上，但是这时不如直接用树上启发式合并，可以做到更好的复杂度。

带修莫队

[国家集训队] 数颜色 / 维护队列。

有 nn 个数，支持询问区间有多少个不同的数和单点修改。

和上一题相比多了一个修改，因此我们来介绍带修莫队：就是多了一个时间轴，排序的时候要看左右端点的块的编号，然后统计答案时直接修正成对应的修改次数。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 2600;

int n, m;
int a[133340], pos[133340], b[133340];
int opp[133340], opv[133340], bck[133340];

struct Operation {
    int l, r, t, id;
    Operation(int l = 0, int r = 0, int t = 0, int id = 0) : l(l), r(r), t(t), id(id) {}
    bool operator < (const Operation &a) const {
        if (pos[l] == pos[a.l]) {
            if (pos[r] == pos[a.r]) return id < a.id;
            return r < a.r;
        }
        return l < a.l;
    }
} Q[133340];
int c1 = 0, c2 = 0;
int Ans[133340], ans, c[1000005];

void update(int p, int f) {
    if (c[p] == 0 && f == 1) ++ans;
    if (c[p] == 1 && f == -1) --ans;
    c[p] += f;
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i), b[i] = a[i];
    for (int i = 1; i <= n; ++i) pos[i] = (i - 1) / BLOCK_SIZE + 1;
    for (int i = 1, x, y; i <= m; ++i) {
        char s[5]; scanf("%s%d%d", s, &x, &y);
        if (s[0] == 'Q') { ++c1; Q[c1] = Operation(x, y, c2, c1); }
        else { ++c2; opp[c2] = x; opv[c2] = y; bck[c2] = b[x]; b[x] = y; }
    }
    sort(Q + 1, Q + c1 + 1); 
    for (int i = 1, l = 1, r = 0, lst = 0; i <= c1; ++i) {
        for (; lst + 1 <= Q[i].t; ++lst) {
            if (l <= opp[lst + 1] && opp[lst + 1] <= r) 
                update(bck[lst + 1], -1), update(opv[lst + 1], 1);
            a[opp[lst + 1]] = opv[lst + 1];
        }
        for (; lst - 1 >= Q[i].t; --lst) {
            if (l <= opp[lst] && opp[lst] <= r)
                update(opv[lst], -1), update(bck[lst], 1);
            a[opp[lst]] = bck[lst];
        }
        for (; r + 1 <= Q[i].r; ++r) update(a[r + 1], 1);
        for (; r - 1 >= Q[i].r; --r) update(a[r], -1);
        for (; l + 1 <= Q[i].l; ++l) update(a[l], -1);
        for (; l - 1 >= Q[i].l; --l) update(a[l - 1], 1);
        Ans[Q[i].id] = ans;
    }
    for (int i = 1; i <= c1; ++i)
        printf("%d\n", Ans[i]);
    return 0;
}

回滚莫队

有的时候增加删除无法简单实现，比如说删除之后你的答案要更新为次大，这就意味着你需要把 kk 大都存下来，这样是无法接受的。这时就需要采用回滚莫队。

[joisc2014] 歴史の研究。

给定一个序列，多次询问区间中重要度（一个数的出现次数乘以自身数值）的最大值。

删除的话可能需要更新为次大值，然而这个东西是没有记录的，这时候需要采用不删除莫队，过程大概像这样：

  1. 排序；
  2. 观察 p=pos[l],q=pos[r]p=pos[l],q=pos[r]，p,qp,q 的位置：
    • 如果 p=qp=q，那么暴力求解；
    • 如果 pp 和上一个询问的 pp 不同，那么将莫队区间的左端点设置为上一个块的右端点 +1，右端点为上一个块的右端点；
    • 否则：
      • 将莫队右端点扩展至询问的右端点，由于右端点是不降的，因此不可能回来；
      • 扩展莫队左端点到询问左端点，并回答询问；
      • 回滚，将莫队的左端点滚回上一个块的右端点 +1。

时间复杂度为 O(nm)O(n\sqrt{m})。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;
const int BLOCK_SIZE = 300;

int n, m, a[100005], b[100005];
int pos[100005], L[1005], R[1005];

struct Quesiton {
    int l, r, id;
    bool operator < (const Quesiton &a) const {
        if (pos[l] == pos[a.l]) return r < a.r;
        return l < a.l;
    }
} Q[100005];

int cnt[100005], _cnt[100005];
i64 Ans[100005], ans;

inline void add(int x, i64 &t) {
    ++cnt[x];
    t = max(t, 1ll * b[x] * cnt[x]);
}

int main(void) {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i), b[i] = a[i];
    sort(b + 1, b + n + 1);
    int tot = unique(b + 1, b + n + 1) - (b + 1);
    for (int i = 1; i <= n; ++i) 
        a[i] = lower_bound(b + 1, b + tot + 1, a[i]) - b;
    for (int i = 1; i <= m; ++i) 
        scanf("%d%d", &Q[i].l, &Q[i].r), Q[i].id = i;
    int t = n / BLOCK_SIZE;
    for (int i = 1; i <= t; ++i) 
        L[i] = R[i - 1] + 1, R[i] = i * BLOCK_SIZE;
    R[t] = n;
    for (int i = 1; i <= t; ++i) 
        for (int j = L[i]; j <= R[i]; ++j) 
            pos[j] = i;
    sort(Q + 1, Q + m + 1);
    for (int i = 1, l = 1, r = 0, last = 0; i <= m; ++i) {
        if (pos[Q[i].l] == pos[Q[i].r]) {
            for (int j = Q[i].l; j <= Q[i].r; ++j) ++_cnt[a[j]];
            for (int j = Q[i].l; j <= Q[i].r; ++j)
                Ans[Q[i].id] = max(Ans[Q[i].id], 1ll * _cnt[a[j]] * b[a[j]]);
            for (int j = Q[i].l; j <= Q[i].r; ++j) --_cnt[a[j]];
            continue;
        }
        if (pos[Q[i].l] != last) {
            for (; l + 1 <= R[pos[Q[i].l]] + 1; ++l) --cnt[a[l]];
            for (; r - 1 >= R[pos[Q[i].l]]; --r) --cnt[a[r]];
            ans = 0; last = pos[Q[i].l];
        }
        for (; r + 1 <= Q[i].r; ++r) add(a[r + 1], ans);

        i64 tmp = ans; int _l = l;
        for (; _l - 1 >= Q[i].l; --_l) add(a[_l - 1], tmp);
        Ans[Q[i].id] = tmp;
        for (; _l + 1 <= l; ++_l) --cnt[a[_l]];
    }
    for (int i = 1; i <= m; ++i)
        printf("%lld\n", Ans[i]);
    return 0;
}

当然类似的还有不添加莫队，请见 Problemset。

莫队二次离线

树分块

Problemset

非常有趣！

简单序列分块

一些简单的分块维护序列的题。

[HNOI2010] 弹飞绵羊

Portal.

分块维护每一个点跳几步跳到块外和跳到块外的位置，时间复杂度 O((n+m)n)O((n+m)\sqrt{n})。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 450; 

int n, m; 
int a[200005], L[2005], R[2005], pos[200005], f[200005], g[200005]; 

int main(void) {
    scanf("%d", &n); int t = (n - 1) / BLOCK_SIZE + 1; 
    for (int i = 1; i <= n; ++i) scanf("%d", a + i); 
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = i * BLOCK_SIZE; R[t] = n; 
    for (int i = 1; i <= t; ++i) for (int j = L[i]; j <= R[i]; ++j) pos[j] = i;
    for (int i = n; i >= 1; --i)
        if (i + a[i] > R[pos[i]]) f[i] = 1, g[i] = i + a[i]; 
        else f[i] = f[i + a[i]] + 1, g[i] = g[i + a[i]]; 
    for (scanf("%d", &m); m--; ) {
        int op, x, y; scanf("%d%d", &op, &x); ++x; 
        if (op == 1) {
            int res = 0; 
            while (g[x] <= n) res += f[x], x = g[x]; 
            printf("%d\n", res + f[x]); 
        } else {
            scanf("%d", &y); a[x] = y; 
            for (int i = R[pos[x]]; i >= L[pos[x]]; --i)
                if (i + a[i] > R[pos[i]]) f[i] = 1, g[i] = i + a[i]; 
                else f[i] = f[i + a[i]] + 1, g[i] = g[i + a[i]]; 
        }
    }
    return 0;
}

[Luogu P3863] 序列

Portal.

如果只有一个数是好做的，对时间进行分块，查询区间的排名。而有多个数，用扫描线来离线维护序列即可（因为是单点查询）。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 
const int BLOCK_SIZE = 300; 

int n, m, t, ans[100005]; 
int L[10005], R[10005], pos[100005]; 
int tot; i64 tag[10005]; 

struct Line {
    int op, t, v; // t 是时间维上的位置
    Line(int op = 0, int t = 0, int v = 0) : op(op), t(t), v(v) {}
};
vector<Line> C[100005]; // 序列维
struct Number {
    int pos; i64 v; 
    bool operator < (const Number &a) const {
        if (v != a.v) return v < a.v; 
        return pos < a.pos; 
    }
} a[100005]; 

void update(int l, int k) { // [x, m] 的时间加上 k
    int p = pos[l]; 
    for (int i = L[p]; i <= R[p]; ++i) if (a[i].pos >= l) a[i].v += k; 
    sort(a + L[p], a + R[p] + 1); 
    for (int i = p + 1; i <= t; ++i) tag[i] += k; 
}
int query(int r, i64 x) { // [1, x] 有多少不小于 y
    int res = 0, p = pos[r]; 
    for (int i = L[p]; i <= R[p]; ++i) if (a[i].pos <= r && a[i].v + tag[p] >= x)  ++res; 
    for (int i = 1; i < p; ++i) 
        res += R[i] - (lower_bound(a + L[i], a + R[i] + 1, Number{0, x - tag[i]}) - a) + 1; 
    return res; 
}

int main(void) {
    memset(ans, -1, sizeof ans); 
    scanf("%d%d", &n, &m); 
    for (int i = 1, x; i <= n; ++i) {
        scanf("%d", &x); 
        C[i].emplace_back(1, 0, x); 
        C[i + 1].emplace_back(1, 0, -x); 
    }
    for (int i = 1; i <= m; ++i) {
        int op, l, r, x; scanf("%d%d", &op, &l);
        if (op == 1) {
            scanf("%d%d", &r, &x); 
            C[l].emplace_back(1, i, x); 
            C[r + 1].emplace_back(1, i, -x); 
        } else {
            scanf("%d", &x); 
            C[l].emplace_back(2, i, x); 
        }
        a[i] = {i, 0}; 
    }
    t = m / BLOCK_SIZE;
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = i * BLOCK_SIZE; 
    if (R[t] < m) { ++t; L[t] = R[t - 1] + 1; R[t] = m; } L[1] = 0; 
    for (int i = 1; i <= t; ++i) for (int j = L[i]; j <= R[i]; ++j) pos[j] = i; 
    for (int i = 1; i <= n; ++i) for (auto it : C[i])
        if (it.op == 1) update(it.t, it.v);
        else ans[it.t] = query(it.t - 1, it.v); 
    for (int i = 1; i <= m; ++i) if (ans[i] != -1) printf("%d\n", ans[i]); 
    return 0;
}

普通莫队

这里是普通莫队。

[SNOI2017] 一个简单的询问

Portal.

给你一个长度为 NN 的序列 aia_i，1≤i≤N1\leq i\leq N，和 qq 组询问，每组询问读入 l1,r1,l2,r2l_1,r_1,l_2,r_2，需输出

∑x=0∞get(l1,r1,x)×get(l2,r2,x)\sum\limits_{x=0}^\infty \text{get}(l_1,r_1,x)\times \text{get}(l_2,r_2,x)

get(l,r,x)\text{get}(l,r,x) 表示计算区间 [l,r][l,r] 中，数字 xx 出现了多少次。

利用差分将 get 拆开，然后就可以直接使用莫队维护了。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64;
const int BLOCK_SIZE = 223;

int n, m;
int a[50005], pos[50005];
i64 Ans[50005], ans;

struct Question {
    int x, y, id, flag;
    Question(int x = 0, int y = 0, int id = 0, int flag = 0) :
        x(x), y(y), id(id), flag(flag) {}
    bool operator < (const Question &a) const {
        if (pos[x] == pos[a.x]) return y < a.y;
        return x < a.x;
    }
} Q[2000005];

int cx[500005], cy[500005];
void updatex(int p, int flag) {
    cx[a[p]] += flag;
    ans += cy[a[p]] * flag;
}
void updatey(int p, int flag) {
    cy[a[p]] += flag;
    ans += cx[a[p]] * flag;
}

int main(void) {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) scanf("%d", a + i);
    for (int i = 1; i <= n; ++i) pos[i] = (i - 1) / BLOCK_SIZE + 1;
    scanf("%d", &m);
    for (int i = 1; i <= m; ++i) {
        int l1, r1, l2, r2; scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
        Q[i * 4 - 3] = Question(r1, r2, i, 1);
        Q[i * 4 - 2] = Question(r1, l2 - 1, i, -1);
        Q[i * 4 - 1] = Question(r2, l1 - 1, i, -1);
        Q[i * 4] = Question(l1 - 1, l2 - 1, i, 1);
    }
    for (int i = 1; i <= m * 4; ++i)
        if (Q[i].x > Q[i].y) swap(Q[i].x, Q[i].y);
    sort(Q + 1, Q + m * 4 + 1);
    for (int i = 1, x = 0, y = 0; i <= m * 4; ++i) {
        for (; x + 1 <= Q[i].x; ++x) updatex(x + 1, 1);
        for (; x - 1 >= Q[i].x; --x) updatex(x, -1);
        for (; y + 1 <= Q[i].y; ++y) updatey(y + 1, 1);
        for (; y - 1 >= Q[i].y; --y) updatey(y, -1);
        Ans[Q[i].id] += ans * Q[i].flag;
    }
    for (int i = 1; i <= m; ++i)
        printf("%lld\n", Ans[i]);
    return 0;
}

[Luogu P3604] 美好的每一天

Portal.

查询的内容非常套路，出现奇数次的字符只能有一个，可以看成区间异或，将字符状压，直接莫队即可。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 500; 

int n, m, pos[60005]; 
uint Ans[60005];
char s[60005]; int a[60005]; 
struct Question {
    int l, r, id; 
    bool operator< (const Question &a) {
        if (pos[l] == pos[a.l]) return r < a.r; 
        return l < a.l;  
    }
} Q[60005];

uint ans, buc[67108870]; 
inline void add(int msk) {
    ans += buc[msk]; ++buc[msk]; 
    for (int i = 0; i < 26; ++i)
        ans += buc[msk ^ (1 << i)]; 
}
inline void del(int msk) {
    --buc[msk]; ans -= buc[msk]; 
    for (int i = 0; i < 26; ++i)
        ans -= buc[msk ^ (1 << i)]; 
}

int main(void) {
    scanf("%d%d%s", &n, &m, s + 1);
    for (int i = 1; i <= n; ++i) {
        a[i] = (1 << s[i] - 'a') ^ a[i - 1]; 
        pos[i] = (i - 1) / BLOCK_SIZE + 1;
    }
    for (int i = 1; i <= m; ++i) scanf("%d%d", &Q[i].l, &Q[i].r), Q[i].id = i; 
    sort(Q + 1, Q + m + 1); 
    for (int i = 1, l = 1, r = 0; i <= m; ++i) {
        while (r < Q[i].r) add(a[++r]); 
        while (r > Q[i].r) del(a[r--]); 
        while (l > Q[i].l - 1) add(a[--l]); 
        while (l < Q[i].l - 1) del(a[l++]); 
        Ans[Q[i].id] = ans; 
    }
    for (int i = 1; i <= m; ++i) printf("%u\n", Ans[i]); 
    return 0;
}

[HNOI2016] 大数

Portal.

设 tit_i 代表 [i,n][i,n] 所代表的数，这样可以直接相减。要求 (tl−tr+1)÷10k≡0(modp)(t_l-t_{r+1})\div 10^{k}\equiv 0\pmod p。两边可以直接相乘，当且仅当 p≠2,p≠5p\ne 2,p\ne 5，这两种情况的答案可以在线计算，剩下的用莫队维护。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 
const int BLOCK_SIZE = 5000; 

int n, p, m, pos[200005]; 
i64 Ans[200005]; 
char s[200005]; 

struct Query {
    int l, r, id; 
    bool operator< (const Query &a) const {
        if (pos[l] == pos[a.l]) return r < a.r; 
        return l < a.l;
    }
} Q[200005];

namespace Subtask {

bool tag[15]; 
i64 cnt[200005], a[200005];
void MAIN(void) {
    if (p == 2) tag[0] = tag[2] = tag[4] = tag[6] = tag[8] = 1; else tag[0] = tag[5] = 1;
    for (int i = 1; i <= n; ++i) {
        a[i] = a[i - 1] + tag[s[i] - '0']; 
        cnt[i] = cnt[i - 1] + tag[s[i] - '0'] * i; 
    }
    while (m--) {
        int l, r; scanf("%d%d", &l, &r); 
        printf("%lld\n", cnt[r] - cnt[l - 1] - (a[r] - a[l - 1]) * (l - 1)); 
    }
}

}

i64 ans; 
int t[200005], c[200005], cnt[200005]; 

inline void add(int x) {
    ans += cnt[x]; 
    ++cnt[x]; 
}
inline void del(int x) {
    --cnt[x]; 
    ans -= cnt[x];
}

int main(void) {
    scanf("%d%s%d", &p, s + 1, &m); n = strlen(s + 1); 
    if (p == 2 || p == 5) return Subtask::MAIN(), 0; 
    for (int i = n, b = 1; i >= 1; --i, b = 10ll * b % p) {
        c[i] = t[i] = (t[i + 1] + 1ll * (s[i] - '0') * b % p) % p; 
        pos[i] = (i - 1) / BLOCK_SIZE + 1; 
    } sort(c + 1, c + n + 2); int nn = unique(c + 1, c + n + 2) - (c + 1); 
    for (int i = 1; i <= n + 1; ++i) t[i] = lower_bound(c + 1, c + nn + 1, t[i]) - c; 
    for (int i = 1; i <= m; ++i) scanf("%d%d", &Q[i].l, &Q[i].r), Q[i].id = i; 
    sort(Q + 1, Q + m + 1);
    for (int i = 1, l = 1, r = 0; i <= m; ++i) {
        ++Q[i].r; 
        for (; r + 1 <= Q[i].r; ++r) add(t[r + 1]); 
        for (; r - 1 >= Q[i].r; --r) del(t[r]); 
        for (; l + 1 <= Q[i].l; ++l) del(t[l]); 
        for (; l - 1 >= Q[i].l; --l) add(t[l - 1]); 
        Ans[Q[i].id] = ans; 
    } 
    for (int i = 1; i <= m; ++i) printf("%d\n", Ans[i]); 
    return 0; 
}

[HNOI2016] 序列

Portal.

考虑设 fl,rf_{l,r} 代表 [l,r][l,r] 的答案，pip_i 为 ii 往前 pi<aip_i<a_i 的 pip_i 最小的位置。那么有 fl,r=fl,pi−1+(i−pi+1)×apif_{l,r}=f_{l,p_i-1}+(i-p_i+1)\times a_{p_i}，整个过程与 ll 无关，因此可以预处理出 f1,if_{1,i}。

考虑莫队维护这个过程。以 rr 的向右增加为例，我们需要统计 ∑i=lrfi,r\sum_{i=l}^r f_{i,r}。找出 [l,r][l,r] 中最小值的位置 pp，对于 fl,r⋯fp,rf_{l,r}\cdots f_{p,r} 答案都是 apa_p。

ll 的移动维护 ff 后缀即可。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 
const int B = 350; 

int n, m; 
int a[100005], pos[100005]; 
struct Query {
    int l, r, id; 
    bool operator< (const Query &a) const {
        if (pos[l] != pos[a.l]) return l < a.l; 
        if (pos[l] & 1) return r < a.r; 
        return r > a.r; 
    }
} Q[100005]; 
i64 ans[100005], pre[100005], nxt[100005]; 
int l[100005], r[100005]; 
int st[100005], tot, f[17][100005]; 
inline int qpos(int l, int r) {
    int k = __lg(r - l + 1); 
    return a[f[k][l]] < a[f[k][r - (1 << k) + 1]] ? f[k][l] : f[k][r - (1 << k) + 1]; 
}

int main(void) {
    ios::sync_with_stdio(0); 
    cin >> n >> m; 
    for (int i = 1; i <= n; ++i) cin >> a[i], f[0][i] = i; 
    for (int i = 1; 1 << i <= n; ++i)
        for (int j = 1; j + (1 << i) - 1 <= n; ++j)
            f[i][j] = (a[f[i - 1][j]] < a[f[i - 1][j + (1 << i - 1)]] ? f[i - 1][j] : f[i - 1][j + (1 << i - 1)]); 

    for (int i = 1; i <= n; ++i) {
        l[i] = i;
        while (l[i] > 1 && a[i] < a[l[i] - 1]) l[i] = l[l[i] - 1];
        pre[i] = pre[l[i] - 1] + 1ll * (i - l[i] + 1) * a[i];
    }
    for (int i = n; i >= 1; --i) {
        r[i] = i;
        while (r[i] < n && a[i] < a[r[i] + 1]) r[i] = r[r[i] + 1];
        nxt[i] = nxt[r[i] + 1] + 1ll * (r[i] - i + 1) * a[i];
    }

    for (int i = 1; i <= n; ++i) pos[i] = (i - 1) / B + 1; 
    for (int i = 1; i <= m; ++i) cin >> Q[i].l >> Q[i].r, Q[i].id = i; 
    sort(Q + 1, Q + m + 1); i64 res = 0; 
    for (int L = 1, R = 0, i = 1; i <= m; ++i) {
        while (R < Q[i].r) {
            ++R; int p = qpos(L, R); 
            res += 1ll * (p - L + 1) * a[p] + pre[R] - pre[p]; 
        }
        while (L > Q[i].l) {
            --L; int p = qpos(L, R); 
            res += 1ll * (R - p + 1) * a[p] + nxt[L] - nxt[p]; 
        }
        while (R > Q[i].r) {
            int p = qpos(L, R); 
            res -= 1ll * (p - L + 1) * a[p] + pre[R] - pre[p]; --R; 
        }
        while (L < Q[i].l) {
            int p = qpos(L, R); 
            res -= 1ll * (R - p + 1) * a[p] + nxt[L] - nxt[p]; ++L; 
        }
        ans[Q[i].id] = res; 
    }
    for (int i = 1; i <= m; ++i) cout << ans[i] << "\n"; 
    return 0;
}

带修莫队

带修莫队的时间复杂度是 O(n53)O(n^{\frac{5}{3}})，块长取 n23n^{\frac{2}{3}}，比较慢。

[WC2013] 糖果公园

Portal.

利用欧拉序将树上的链拍到线性结构上。发现链的处理方式是链的两个端点第一次出现位置的一段（LCA 要讨论）。然后直接带修莫队。

查看代码 
#include <bits/stdc++.h>
using namespace std;
typedef long long i64; 
const int BLOCK_SIZE = 3000; 

int n, m, q, pos[200005], lg[100005]; 
int idx[200005], tot, siz[100005], dep[100005]; 
int mi[17][100005], dfn[100005], num; 
int L[100005], R[100005]; 
int v[100005], w[100005], a[100005]; 
vector<int> G[100005]; 

inline int get(int x, int y) { return dep[x] < dep[y] ? x : y; }
void dfs(int x, int fa) {
    idx[++tot] = x; L[x] = tot; 
    mi[0][dfn[x] = ++num] = fa; siz[x] = 1; dep[x] = dep[fa] + 1; 
    for (int y : G[x]) if (y != fa) {
        dfs(y, x); siz[x] += siz[y]; 
    }
    idx[++tot] = x; R[x] = tot; 
}
int LCA(int u, int v) {
    if (u == v) return u; 
    if ((u = dfn[u]) > (v = dfn[v])) swap(u, v); 
    int k = lg[v - u]; 
    return get(mi[k][u + 1], mi[k][v - (1 << k) + 1]); 
}

struct Operation {
    int l, r, lca, time, id; 
    bool operator< (const Operation &a) const {
        if (pos[l] == pos[a.l]) {
        	if (pos[r] == pos[a.r]) return time < a.time; 
        	return r < a.r; 
		}
		return l < a.l; 
    }
} Q[100005]; 
struct Change {
    int x, y; 
} C[100005];
int c1, c2; 

i64 Ans[100005], ans; 
bool vis[100005]; int cnt[100005]; 
inline void modify(int x) {
	if (vis[x]) ans -= 1ll * v[a[x]] * w[cnt[a[x]]--]; 
	else ans += 1ll * v[a[x]] * w[++cnt[a[x]]]; 
    vis[x] ^= 1; 
}
inline void update(int x) {
	if (vis[C[x].x]) {
		modify(C[x].x); 
		swap(C[x].y, a[C[x].x]); 
		modify(C[x].x); 
	} else swap(C[x].y, a[C[x].x]); 
}

int main(void) {
    scanf("%d%d%d", &n, &m, &q); 
    for (int i = 2; i <= n; ++i) lg[i] = lg[i >> 1] + 1; 
    for (int i = 1; i <= m; ++i) scanf("%d", v + i); 
    for (int i = 1; i <= n; ++i) scanf("%d", w + i); 
    for (int i = 1; i < n; ++i) {
        int u, v; scanf("%d%d", &u, &v); 
        G[u].emplace_back(v); G[v].emplace_back(u); 
    } dfs(1, 0); 
    for (int i = 1; i <= n; ++i) scanf("%d", a + i); 
    for (int i = 1; i <= lg[n]; ++i)
        for (int j = 1; j + (1 << i) - 1 <= n; ++j)
            mi[i][j] = get(mi[i - 1][j], mi[i - 1][j + (1 << i - 1)]); 

    for (int i = 1; i <= q; ++i) {
        int op, x, y; scanf("%d%d%d", &op, &x, &y); 
        if (op == 1) {
            if (L[x] > L[y]) swap(x, y); int d = LCA(x, y); ++c1; 
            if (x == d) Q[c1].l = L[x], Q[c1].r = L[y]; 
            else Q[c1].l = R[x], Q[c1].r = L[y], Q[c1].lca = d; 
            Q[c1].id = c1; Q[c1].time = c2; 
        } else { C[++c2] = {x, y}; }
    } 
    for (int i = 1; i <= tot; ++i) pos[i] = (i - 1) / BLOCK_SIZE + 1; 
    sort(Q + 1, Q + c1 + 1); 

    for (int i = 1, l = 1, r = 0, lst = 0; i <= c1; ++i) {
        while (r < Q[i].r) modify(idx[++r]); 
        while (r > Q[i].r) modify(idx[r--]); 
        while (l < Q[i].l) modify(idx[l++]); 
        while (l > Q[i].l) modify(idx[--l]); 
        while (lst < Q[i].time) update(++lst); 
        while (lst > Q[i].time) update(lst--);  
        if (Q[i].lca) modify(Q[i].lca); 
        Ans[Q[i].id] = ans;
        if (Q[i].lca) modify(Q[i].lca); 
    }
    
    for (int i = 1; i <= c1; ++i) printf("%lld\n", Ans[i]); 
    return 0;
}

回滚莫队

这里是回滚莫队。

【模板】回滚莫队 & 不删除莫队

Portal.

可以再练习一下。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 400;
const int INF = 0x3f3f3f3f;

int n, m;
int a[200005], b[200005];
int pos[200005], L[1000], R[1000];

struct Question {
    int l, r, id;
    bool operator < (const Question &a) const {
        if (pos[l] == pos[a.l]) return r < a.r;
        return l < a.l;
    }
} Q[200005];

int Ans[200005], ans;
int st[200005], ed[200005], tpst[200005], tped[200005];
int vis[200005], lst[200005];

int main(void) {
    scanf("%d", &n);
    int t = n / BLOCK_SIZE;
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = i * BLOCK_SIZE; R[t] = n;
    for (int i = 1; i <= t; ++i) 
        for (int j = L[i]; j <= R[i]; ++j) 
            pos[j] = i;

    for (int i = 1; i <= n; ++i) scanf("%d", a + i), b[i] = a[i];
    sort(b + 1, b + n + 1);
    int tot = unique(b + 1, b + n + 1) - (b + 1);
    for (int i = 1; i <= n; ++i)
        st[a[i] = lower_bound(b + 1, b + tot + 1, a[i]) - b] = INF;

    scanf("%d", &m);
    for (int i = 1; i <= m; ++i) 
        scanf("%d%d", &Q[i].l, &Q[i].r), Q[i].id = i;
    sort(Q + 1, Q + m + 1);

    memset(st, 0x3f, sizeof(st));
    for (int i = 1, l = 1, r = 0, last = 0; i <= m; ++i) {
        if (pos[Q[i].l] == pos[Q[i].r]) {
            int res = 0;
            for (int j = Q[i].l; j <= Q[i].r; ++j) lst[a[j]] = j;
            for (int j = Q[i].l; j <= Q[i].r; ++j) res = max(res, lst[a[j]] - j);
            for (int j = Q[i].l; j <= Q[i].r; ++j) lst[a[j]] = 0;
            Ans[Q[i].id] = res;
            continue;
        }
        if (pos[Q[i].l] != last) {
            memset(st, 0x3f, sizeof(st));
            memset(ed, 0, sizeof(ed));
            last = pos[Q[i].l]; ans = 0;
            l = R[last] + 1, r = R[last];
        }
        for (; r + 1 <= Q[i].r; ++r) {
            int p = r + 1;
            st[a[p]] = min(st[a[p]], p);
            ed[a[p]] = max(ed[a[p]], p);
            ans = max(ans, ed[a[p]] - st[a[p]]);
        }
        int _l = l, tmp = ans;
        for (; _l - 1 >= Q[i].l; --_l) {
            int p = _l - 1;
            if (vis[a[p]] != i) {
                vis[a[p]] = i;
                tpst[a[p]] = st[a[p]], tped[a[p]] = ed[a[p]];
            }
            tpst[a[p]] = min(tpst[a[p]], p), tped[a[p]] = max(tped[a[p]], p);
            tmp = max(tmp, tped[a[p]] - tpst[a[p]]);
        }
        Ans[Q[i].id] = tmp;
    }
    for (int i = 1; i <= m; ++i) 
        printf("%d\n", Ans[i]);
    return 0;
}

复杂问题

一些比较困难的问题。

「RdOI R3.5」RMSQ

Portal.

将 aa 重新编号，问题转化为求区间最长连续子序列。

考虑暴力进行 DP：设 fif_i 代表以 ii 结尾的数的最大答案，那么 fi=fi−1+1f_{i}=f_{i-1}+1。

将原序列分块，如果没有整块则直接暴力，否则考率预处理出整块的答案，然后将零散块的答案合并进整块。可是怎么合并？好像不太好做，我们无法高效预处理出整块的 DP 值，无法对散块进行 DP。

想想有没有简单的方法，我们在扩展右区间时，会对整块内的元素产生贡献，也会对右区间自己产生贡献。整块的元素并不会改变！我们只需要预处理出某一个整块到 ii 的 DP 数组即可！转移也要发生改变，设 fif_i 代表以 ii 开始的最大答案，这样计算很方便。

同理，我们预处理出每一个整块到序列开头的 DP 数组，然后直接合并即可。可以将这一个 DP 数组存到下个整块的记录到 ii 的 DP 数组中（因为它们没有重合部分）。

这样就以 O(nn)O(n\sqrt{n}) 在线解决了这个问题。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 450;

inline int read(void) {
    int x = 0, c = getchar(); 
    while (!isdigit(c)) c = getchar(); 
    while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar(); 
    return x; 
}

int m, n, q, T, tmp[300005], f[300005]; 
int b[300005], a[300005], bb[300005], Ans[805][805]; 
int pos[300005], L[805], R[805], ls[300005], rs[300005]; 
int pd[805][300005]; // pd[i] 记录 i 到末尾的 DP，pd[i + 1] 记录块 i 尾到头部的 DP 

inline int query(int l, int r) {
    int p = pos[l] + 1, q = pos[r] - 1, ans = 0; // 整块左端和右端 
    if (p > q) {
        for (int i = l; i <= r; ++i) ans = max(ans, f[a[i]] = f[a[i] - 1] + 1);
        for (int i = l; i <= r; ++i) f[a[i]] = 0; 
        return ans;  
    } ans = Ans[p][q]; 
    // 右区间扩展
    // 对整块贡献，对右散块之前的元素贡献 
    for (int i = R[q] + 1; i <= r; ++i) {
    	f[a[i] - pd[p][i] + 1] = max(f[a[i] - pd[p][i] + 1], pd[p][i]); 
    	ans = max(ans, f[a[i] - pd[p][i] + 1]); 
	}
	// 左区间扩展
	// 自己贡献，对右散块贡献 | 对整块贡献 
    for (int i = L[p] - 1; i >= l; --i) {
    	f[a[i]] = max({f[a[i]], f[a[i] + 1] + 1, pd[q + 1][i]}); // prer[q][i]
    	ans = max(ans, f[a[i]]); 
	} 
    for (int i = R[q] + 1; i <= r; ++i) f[a[i] - pd[p][i] + 1] = 0; 
    for (int i = L[p] - 1; i >= l; --i) f[a[i]] = 0; 
    return ans; 
}

int main(void) {
    m = read(), n = read(), q = read(), T = read();  
    for (int i = 1; i <= m; ++i) b[read()] = i; 
    for (int i = 1; i <= n; ++i) a[i] = b[read()]; 
    int t = n / BLOCK_SIZE; 
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = i * BLOCK_SIZE; 
    if (R[t] < n) { ++t; L[t] = R[t - 1] + 1; R[t] = n; }
    for (int i = 1; i <= t; ++i) for (int j = L[i]; j <= R[i]; ++j) pos[j] = i; 
    
    for (int i = 1; i <= n; ++i) ls[i] = tmp[a[i] - 1], tmp[a[i]] = i; 
    memset(tmp, 0, sizeof tmp); 
    for (int i = n; i >= 1; --i) rs[i] = tmp[a[i] + 1], tmp[a[i]] = i; 
    
    for (int l = 1; l <= n; l += BLOCK_SIZE) {
        int ans = 0; int *dp = pd[pos[l]]; // 维护第 l 块到末尾的 DP 数组 
        for (int r = l; r <= n; ++r) {
            ans = max(ans, dp[r] = dp[ls[r]] + 1); 
            if (pos[r] != pos[r + 1]) Ans[pos[l]][pos[r]] = ans; 
        }
    }
    for (int r = BLOCK_SIZE; r <= n; r += BLOCK_SIZE) {
    	int *dp = pd[pos[r] + 1]; 
    	for (int l = r; l >= 1; --l) f[l] = f[rs[l]] + 1; 
    	for (int l = r; l >= 1; --l) dp[l] = f[l]; 
    	memset(f, 0, sizeof f); 
	}

    for (int last = 0; q--; ) {
        int l = read(), r = read(); if (T) l ^= last, r ^= last; 
        printf("%d\n", last = query(l, r)); 
    }
    return 0; 
}

[Ynoi2007] rfplca

Portal.

维护一个数的父亲和跳出块内的父亲。散块暴力重构块的信息，整块被修改块长次以上后会直接跳出块，父亲值可以直接计算。查询时最多跳块的个数次。时间复杂度 O(nn)O(n\sqrt{n})。

查看代码 
#include <bits/stdc++.h>
using namespace std;
const int BLOCK_SIZE = 600; 

int n, m;
int fa[400005], L[4005], R[4005], tag[4005], c[4005], pos[400005], pa[400005]; 

inline void change(int i) {
    if (pos[i] == pos[fa[i]]) pa[i] = pa[fa[i]]; 
    else pa[i] = fa[i]; 
}
void rebuild(int l, int r, int x) {
    for (int i = l; i <= r; ++i) fa[i] = max(fa[i] - x, 1); 
    for (int i = l; i <= R[pos[l]]; ++i) change(i); 
}
void update(int l, int r, int x) {
    int p = pos[l], q = pos[r]; 
    if (p == q) return rebuild(l, r, x); 
    rebuild(l, R[p], x); rebuild(L[q], r, x); 

    for (int i = p + 1; i < q; ++i) {
        if (c[i] <= BLOCK_SIZE) {
            for (int j = L[i]; j <= R[i]; ++j)
                fa[j] = max(fa[j] - x, 1), change(j); 
        } else tag[i] = min(tag[i] + x, n); 
        ++c[i]; 
    }
}
inline int Pa(int x) {
    if (c[pos[x]] <= BLOCK_SIZE) return pa[x]; 
    return max(1, fa[x] - tag[pos[x]]); 
}
inline int Fa(int x) {
    if (c[pos[x]] <= BLOCK_SIZE) return fa[x]; 
    return max(1, fa[x] - tag[pos[x]]); 
}
int query(int u, int v) {
    while (u != v) {
        int pu = Pa(u), pv = Pa(v); 
        if (pos[pu] != pos[pv]) pos[pu] < pos[pv] ? v = pv : u = pu; 
        else if (pu != pv) pu < pv ? v = pv : u = pu; 
        else u < v ? v = Fa(v) : u = Fa(u); 
    }
    return u; 
}

int main(void) {
    scanf("%d%d", &n, &m); fa[1] = pa[1] = 1; int t = (n - 1) / BLOCK_SIZE + 1; 
    for (int i = 1; i <= t; ++i) L[i] = R[i - 1] + 1, R[i] = i * BLOCK_SIZE; R[t] = n; 
    for (int i = 1; i <= t; ++i) for (int j = L[i]; j <= R[i]; ++j) pos[j] = i; 
    for (int i = 2; i <= n; ++i) scanf("%d", fa + i), change(i); 
    for (int last = 0; m--; ) {
        int op, l, r, x; scanf("%d%d%d", &op, &l, &r); l ^= last, r ^= last; 
        if (op == 1) scanf("%d", &x), x ^= last, update(l, r, x); 
        else printf("%d\n", last = query(l, r)); 
    }
    return 0;
}
块状数据结构
https://james1badcreeper.github.io/f2886e9e/
本文作者
james1BadCreeper
发布于
2023年3月1日
许可协议
CC BY-NC-SA 4.0
署名-非商业性使用-相同方式共享 4.0 国际。

发布于 2023年3月1日
算法竞赛学习笔记数据结构

分块

数据结构f

评论

若无法加载，请尝试刷新，欢迎讨论、交流和提出意见，支持 Markdown 与 LaTeX 语法（公式与文字间必须有空格）！